Интегрирование по частям.
Неопределенный интеграл и его свойства.
Определение 1.: Функция F(x) называется первообразной для функции ƒ(x) на некотором отрезке [a,b], если для всех из этого отрезка выполняется равенство:
F'(x)= ƒ(x).
Пример: F(x)=cos(x)+C; ƒ(x)=sin(x);
Теорема1. Если F1(x) и F2(x) какие-либо первообразные для функции ƒ(x) на отрезке [a,b], то выполняется соотношение:
F1(x) – F2(x) = C;
Доказательство.
Так как F1(x) первообразная для функции ƒ(x), то F1'(x)= ƒ(x).
Так как F2(x) первообразная для функции ƒ(x), то F2'(x)= ƒ(x).
Вычтем из первого равенства второе:
F1' (x) – F2'(x) = 0,
(F1(x) – F2(x))' = 0;
Обозначим F1(x) – F2(x)=φ(x), тогда φ'(x)=0;
Покажем, что φ(x) принимает постоянные значения.
Применим φ(x) на отрезке [a,x] теорему Лагранжа.
φ(x) – φ(a) = φ'(ξ)(x-a), a< ξ <x ,
так как φ'(ξ)=0, то φ(x) – φ(a) =0, то есть φ(x) = φ(a).
φ(a) = С, φ(x) =С;
F1(x) – F2(x) = C;
Замечание:из теоремы следует, что, если F(x) первообразная для ƒ(x), то (F(x)+С ) тоже первообразная.
Определение 2.: Совокупность первообразных, т.е. (F(x)+С), для ƒ(x) на [a,b] называется неопределенным интегралом от f(x) и обозначается:
∫ƒ(x) dx = F(x) + C, причем F'(x) = ƒ(x),
ƒ(x) – называется подынтегральной функцией;
ƒ(x)dx – называется подынтегральным выражением;
Свойства неопределенного интеграла:
1.(∫ƒ(x)dx)' = ƒ(x);
Доказательство.
(∫ƒ(x)dx)' = (F(x)+C)' = F'(x) = ƒ(x);
2. d ∫ƒ(x)dx = ƒ(x)dx;
Доказательство.
d∫ƒ(x)dx = (∫ƒ(x)dx)' · dx = | по свойству 1| = ƒ(x)dx;
3. ∫d F(x) = F(x) + C;
Доказательство.
Возьмем дифференциал от левой части:
d ∫dF(x) = dF(x) (по свойству 2 )
найдем дифференциал от правой части:
d (F(x) + C) = dF(x) + dC = dF(x)
Получили, что обе части равны.
4. ∫(ƒ1(x)+ ƒ2(x))dx = ∫ƒ1(x)dx + ∫ƒ2(x)dx.
Найдем производную от левой и от правой частей:
(∫(ƒ1(x)+ ƒ2(x))dx)' = |по св-ву 1| = ƒ1(x)+ ƒ2(x)
(∫ƒ1(x)dx + ∫ƒ2(x)dx)' = (∫ƒ1(x)dx + ∫ƒ2(x)dx)' = ƒ1(x) + ƒ2(x).
5. ∫k·ƒ(x)dx = k·∫ƒ(x)dx, где k – постоянный множитель.
Доказательство.
(∫k·ƒ(x)dx)' = k·ƒ(x);
(k·∫ƒ(x)dx)' = k·(∫ƒ(x)dx)' = k·∫ƒ(x);
6. Формулы интегрирования не меняет свой вид при подстановке вместо независимой переменной x некоторой функции u(x), т.е. если ∫ƒ(x)dx = F(x) + C;
∫ƒ(u)du = F(u) + C;
Доказательство.
Имеем: ∫ƒ(x)dx = F(x) + C;
F'(x) = ƒ(x),
Так как дифференциал первого порядка обладает свойством инвариантности, т.е. форма его не зависит от того является ли x независимой переменной или некоторой функцией
от x, то дифференциал
dF(u) = F'(u)du = ƒ(u)du
F'(u) = ƒ(u)
∫ƒ(u)du = ∫dF(u) = | по свойству 3 | = F(u) + C.
Таблица основных интегралов.
| 1. ∫ xαdx = xα+1/ (α+1) + C α ≠-1 | 1. ∫ uα du = uα+1/ (α+1) + C α ≠-1 |
2. 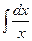 = ln |x| + C = ln |x| + C
| 2. 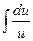 = ln |u| + C = ln |u| + C
|
| 3. ∫ ex= ex + C | 3. ∫ eu = eu + C |
| 4. ∫ ax dx = ax/lna + C | 4. audu = au/lna + C |
| 5. ∫sin(x)dx = - cos(x) + C | 5. ∫sin(u)du= - cos(u) + C |
| 6. ∫cos(x)dx = sin(x) + C | 6. ∫cos(u)du = sin(u) + C |
7. 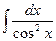 = tg(x) + C = tg(x) + C
| 7. 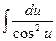 = tg(u) + C = tg(u) + C
|
8. 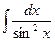 = -ctg(x) + C = -ctg(x) + C
| 8. 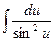 = -ctg(u) + C = -ctg(u) + C
|
 9. 9. 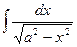 = arcsin ( = arcsin ( 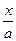 )+ C )+ C
| 9. 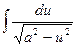 = arcsin ( = arcsin ( 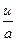 )+C )+C
|
10. 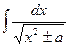 = ln | x + = ln | x + 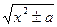 | + C | + C
| 10. 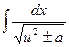 = ln |u + = ln |u + 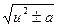 | + C | + C
|
11. 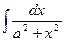 = = 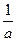 arctg( arctg( 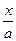 )+C )+C
| 11. 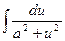 = = 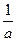 arctg( arctg( 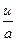 )+C )+C
|
12. 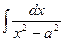 = = 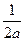 ln | ln | 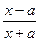 | + C | + C
| 12. 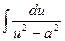 = = 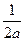 ln | ln | 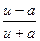 | + C | + C
|
13 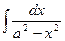 = = 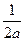 ln | ln | 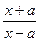 | + C | + C
| 13. 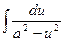 = = 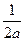 ln | ln | 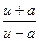 | + C | + C
|
14. 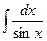 = ln |tg( = ln |tg( 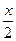 )| + C )| + C
| 14. 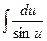 = ln |tg( = ln |tg( 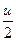 )| + C )| + C
|
15. 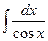 = ln |tg( = ln |tg( 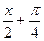 )| + C )| + C
| 15. 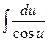 = ln |tg( = ln |tg( 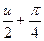 )| + C )| + C
|
| 16.∫ tg(x) dx = – ln |cos(x)| + C | 16.∫tg(u) du = – ln |cos(u)| + C |
| 17.∫ ctg(x) dx = ln |sin(x)| + C | 17.∫ ctg(u) du = ln |sin(u)| + C |
Проверим формулу 9.
(arcsin 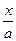 )' =
)' = 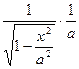 =
= 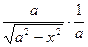 =
= 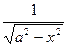 ;
;
Проверим формулу 10.
(ln| x + 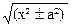 | )' =
| )' = 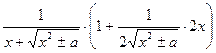 =
= 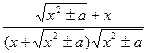 =
= 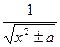 ;
;
Проверим формулу 11.
( 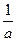 arctg
arctg 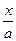 )' =
)' = 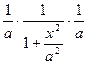 =
= 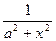 ;
;
Поверим формулу 12.
( 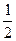 a ∙ ln |
a ∙ ln | 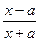 |)' =
|)' = 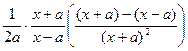 =
= 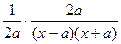 =
= 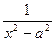 ;
;
Проверим формулу 14.
(ln |tg( 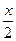 )|)' =
)|)' = 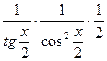 =
= 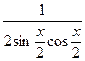 =
= 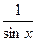 ;
;
Проверим формулу 15.
Пусть cos(x) = sin(x + 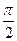 )
)
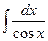 =
= 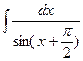 = ln |tg(
= ln |tg( 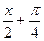 )| + C;
)| + C;
Проверим формулу 16.
∫tg(x) dx = ∫ 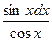 = – ∫ –
= – ∫ – 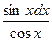 = - ∫
= - ∫ 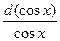 = – ∫
= – ∫ 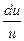 = – ln |cos(x)| + C;
= – ln |cos(x)| + C;
Проверим формулу 17.
∫ ctg(x) dx = ∫ 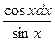 = ∫
= ∫ 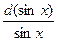 = =ln |sin(x)| + C;
= =ln |sin(x)| + C;
Пример:
1. ∫ 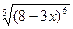 dx = ∫(8-3x)6/5 dx = | d(8-3x) = – 3dx | = –
dx = ∫(8-3x)6/5 dx = | d(8-3x) = – 3dx | = – 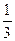 ∫(8-3x)6/5 (– 3dx) =
∫(8-3x)6/5 (– 3dx) =
– 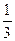 ∫(8 –3x)6/5 d(8-3x) = –
∫(8 –3x)6/5 d(8-3x) = – 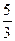 (8-3x)11/5 + C.
(8-3x)11/5 + C.
_____
2. ∫x√4 + x² dx = ∫(4 + x²)1/2x dx = | d(4 + x²) = 2x dx| = 1/2 · ∫(4 + x²)1/22x dx =
= 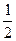 ·∫(4 + x²)1/2 d(4 + x²) =
·∫(4 + x²)1/2 d(4 + x²) = 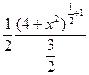 =
= 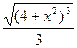 + C;
+ C;
______
3. ∫3√sin²(x) · cos(x)dx = ∫(sin(x))2/3 d(sin(x)) = 5/3 (sin(x))5/3 + C
4. Найти интеграл.
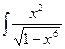 dx=
dx= 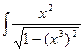 dx = |
dx = | 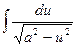 | =
| = 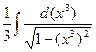 =
= 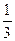 arcsin (x3) + C.
arcsin (x3) + C.
§2. Замена переменной в неопределенном интеграле (метод подстановки).
Теорема.: Пусть функция x = φ(t) – строго монотонная и непрерывно дифференцируемая на некотором интервале функции φ(t). Если функция ƒ(x) интегрируема на соответствующем интервале изменений x, то имеет место равенство:
∫ƒ(x)dx = ∫ƒ(φ(t))·φ'(t)dt
Доказательство.
Определени1: Если функция ƒ(x) непрерывна на отрезке [a,b], то существует неопределенный интеграл ∫ƒ(x)dx, а функция ƒ(x) в этом случае называется интегрируемой.
По определению1 неопределенного интеграла
∫ƒ(x)dx = F(x) + C, причем F'(x) = ƒ(x)
Покажем, что функция F(φ(t)) является первообразной для функции: ƒ(φ(t))·φ'(t).
Для этого найдем (F(φ(t)))' = |по правилу дифференцирования сложной функции| =
= F'(φ(t))·φ'(t);
Но F'(φ(t)) = ƒ (φ(t)), тогда
(F(φ(t)))' = ƒ(φ(t))·φ'(t)
∫ƒ(φ(t))·φ'(t) dt = F(φ(t)) + C = F(x) + C = ∫ƒ(x) dx.
∫ƒ(x) dx = ∫ƒ(φ(t)) ·φ'(t) dt.
Пример:
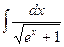 = | ex +1 = t2 ;
= | ex +1 = t2 ; 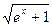 = t ; ex = t2 – 1 ; x = ln(t2 –1 ) ; dx =
= t ; ex = t2 – 1 ; x = ln(t2 –1 ) ; dx = 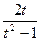 dt | =
dt | =
= 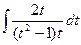 = 2
= 2 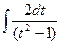 = 2∙
= 2∙ 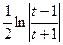 =
= 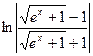 +C.
+C.
Интегрирование по частям.
Пусть U(x) и V(x) дифференцируемые функции на некотором интервале, известно, что
d(UV) = U ∙ dV + V ∙ dU.
Проинтегрируем это равенство:
∫d(UV) = ∫U ∙ dV + ∫V ∙ dU ;
UV = ∫U ∙ dV + ∫V ∙ dU ;
∫U ∙ dV = UV - ∫V ∙ dU –формула интегрирования по частям.
Пример:вычислить∫x · sin(x) dx
I способ.
∫x · sin(x) dx = | U=x; dU = dx; dV = sin(x) dx; ∫dV= ∫sin(x) dx;V = -cos(x)| =
= -x · cos(x) - ∫(- cos(x)) dx= -x · cos(x) + sin(x) + C;
II способ.
∫x · sin(x) dx = | U = sin(x); dU=cos(x) dx; dV=x dx; V=∫x dx = 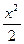 ; | =
; | = 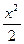 · sin(x) –
· sin(x) –
∫ 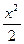 · cos(x) dx.
· cos(x) dx.
Замечание:классы функций интегрируем по частям.
I класс – это интегралы вида:
∫Pn(x) · eax dx;
∫Pn(x) · sin(a·x) dx;
∫Pn(x) · cos(a·x)dx , где Pn(x) – это многочлен первой степени, в этом случае U = Pn(x);
II класс – это интегралы вида:
1.∫Pn(x) · ln(a·x) dx;
2.∫Pn(x) · arcsin(x) dx;
3.∫Pn(x) · arctg(x) dx , где в качестве 1.U = ln(a·x); 2.U = arcsin(x); 3.U = arctg(x);
Пример:
∫x2 · ln(1+x) dx ;
∫x2 · ln(1+x) dx = | U= ln(1+x); dU= 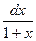 ; dV = x2 dx; V=
; dV = x2 dx; V= 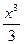 ; | = ln(1+x) ·
; | = ln(1+x) · 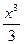 –
–
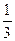 · ∫
· ∫ 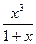 dx = | выделим целую часть:
dx = | выделим целую часть:
x3 |x+1
¯ x3+x2 x2-x+1
- x2
¯- x2–x_
x
¯ x+1
-1
значит, _ x3_ = x2 – x +1 + -1_ ; | =
x+1 x+1
= 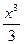 ·ln(1+x) –
·ln(1+x) – 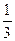
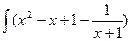 dx =
dx = 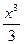 ·ln(1+x) –
·ln(1+x) – 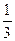 ·
· 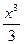 +
+ 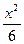 –
– 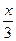 +
+ 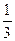 ·
· 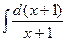 =
=
= 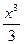 ·ln(1+x) –
·ln(1+x) – 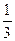 ·
· 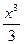 +
+ 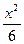 –
– 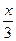 +
+ 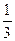 ·ln(x+1) +C;
·ln(x+1) +C;
Пример2: интеграл вида:
∫ex · sin(x) dx = | U = ex; dU= exdx; dV= sin(x) dx; V=∫sin(x) dx = –cos(x); | = –ex · cos(x) + + ex · sin(x) – ∫ex · sin(x) dx;
∫ex · sin(x) dx = –ex · cos(x) + + ex · sin(x) – ∫ex · sin(x) dx;
получили уравнение относительно интеграла, неизвестным является интеграл.
2 ∫ex · sin(x) dx = ex · (sin(x) – cos(x) );
∫ex · sin(x) dx = 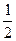 · ex · (sin(x) – cos(x) ) + C;
· ex · (sin(x) – cos(x) ) + C;
Дата добавления: 2015-12-16; просмотров: 754;
