Интегрирование импульсных сигналов

Интегрирующей цепью называется четырехполюсник, сигнал на выходе которого пропорционален интегралу от входного сигнала:

u_ВЫХ(t) = K× 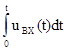(1.10)

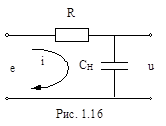
При подаче на цепь напряжения e выходной сигнал u снимается с конденсатора C:

u= 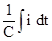, u(0)=0 (1.10’)

где i = 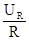¾ ток, проходящий по цепи; U_R=e-u ¾ напряжение на активном сопротивлении; Т = RC — постоянная времени интегрирующей цепочки. Подставляя выражения для i, U и T в (1.10), получим

u= 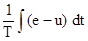(1.11)

Условие u << e является условием правильного интегрирования, т.е. u ~ 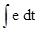. Для выполнения этого условия нужно уменьшить напряжение на выходе u за счет увеличения емкости С и уменьшения тока i, которое происходит при увеличении сопротивления R. Для выполнения условия интегрирования нужно увеличивать постоянную времени интегрирующей цепочки.

Коэффициент передачи интегрирующей цепочки:

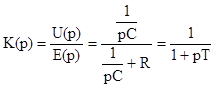, (1.12)

K(jw)= 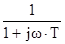. (1.13)

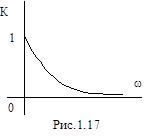
Зависимость коэффициента передачи от частоты представлена на рис.1.17, откуда можно видеть, что условие интегрирования выполняется лучше для высоких частот, т.к. чем больше w, тем меньше К(р) и, следовательно, меньше U(p) = К(р)×Е(р).

Будем считать, что на вход цепочки подается сигнал e(t) = a×t, изображение которого Е(р) = a/р² . Изображение снимаемого напряжения

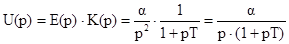, (1.14)

а величина снимаемого напряжения (рис.1.10) определяется как

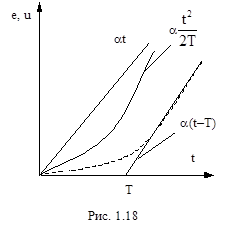
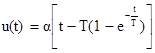. (1.15)

При условии, что 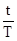<<1 можно разложить функцию 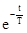в степенной ряд. Тогда получим

u(t) » 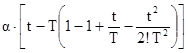= 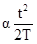(1.16)

На рис. 1.18 показаны зависимости e(t) и u(t) для условия t<<T и при t=3…5×T, чему соответствует уравнение u(t)=a(t‑T).

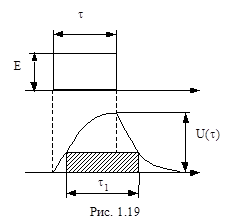
Если подать на вход интегрирующей цепи прямоугольный импульс, то, согласно (1.10),

u_ВЫХ(t) = K× 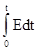= K×E×t при 0 < t < t

u_ВЫХ(t) = K×E×t = const при t > t.

В реальном случае

u_ВЫХ(t) = E× 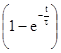при 0 < t < t

u_ВЫХ(t) = E× 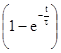× 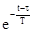=U(t)× 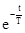при t > t.

Если поставить в цепь ограничитель, то получим на выходе импульс длительности t₁>t, но по амплитуде меньше входного импульса.