Временные характеристики стохастических сигналов

Описание стохастических сигналов как функции времени в де­терминированном виде невозможно. Вместо этого проводится стати­стическое описание. При этом предполагается, что сигнал является стационарным.

Первой характеристикой стохастического сигнала является амплитудная плотность. Если амплитуды сигнала разбить на интервалы шириной 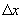, то можно опреде­лить относительную частоту для каждого интервала:

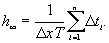
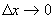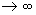Аналогично процедуре, изложенной ранее, можно, осуществляя предельный переход и Т , получить в общем случае непрерывную функцию амплитудной плотности:

.

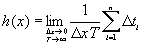Среднее значение сигнала, определяемое в результате усреднения по времени, соответствует первому моменту плотности распределения, так как площадь под графиком плотности распре­деления равна единице:

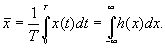
Дисперсия сигнала представляет собой среднеквадратичное отклонение амплитуды от среднего значения. Это величина соответствует второму моменту плотности распределения относи­тельно центра тяжести распределения :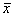

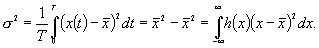(5.1)

Разумеется, что характеристика сигнала c помощью только плотности амплитуд связана с известной потерей информации. Одному и тому же распределению плотности амплитуд может соответствовать бесконечное множество форм сигнала. И, что особенно важно, плотность амплитуд никак не характеризует тенденцию изменения сигнала во времени. Быстро изменяющийся сигнал может иметь то же самое распределение плотности амплитуд_, что и медленно изменяющийся сигнал.

Корреляционная функция. Для оценки «тенденции сигнала к сохранению», которую также называют внутренней когерентностью, может быть использовано понятие корреляции.

При изучении вопроса о наличии линейной статистической связи между парами значени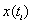й и 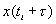рассчитывают упомянутый ранее коэффициент корреляции. Чем теснее линейная зависимость, тем больше модуль коэффициента корреляции, тем с большей вероятностью на основе значений функции 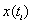в мо­мент времени 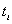возможен прогноз 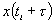в момент времени 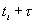. Он состоит в том, что в течение отрезка времени 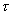сигнал имеет тенденцию к сохранению.

Изучаемый отрезок времени 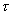— свободная (независимая) пере­менная. Таким образом, коэффициент корреляции является функ­цией переменной 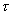. В рассматриваемом случае говорят об авто­корреляционной функции. В отличие от коэффициента корреляции дискретных пар значений автокорреляционная функция в общем случае относится к непрерывному сигналу 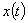и часто не норми­руется. Как и при расчете среднего значения и дис­персии, сумма дискретных значений заменяется интег­ралом

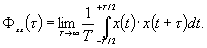(5.2)

Исходя из изложенного, можно ожидать, что в общем случае для больших сдвигов времени 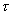тенденция к сохранению сигнала становится меньше. Действительно, можно показать, что 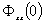есть максимум функции и справедливо следующее неравенство:

.

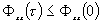Как следует из (5.2), 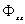(0) = 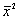соответствует среднему значению квадрата функции :

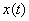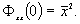
Далее имеет место равенство

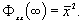
Для дисперсии, рассчитанной по (5.1), справедливо соот­ношение:

.

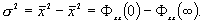Очевидно, автокорреляционная функция является четной функцией :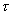

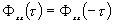
Рисунок 5.3- Примеры сигналов и их автокорреляционных функций

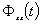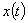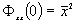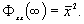является характеристической функцией изучаемого стохастического сигнала . Тенденция сигнала к сохранению (рисунок 5.3, а и б) характеризуется видом автокорреляции одной функции между точками и Если 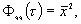то это означает, что пары значени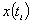й и 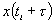не коррелированы.

Разумеется, зависимость (5.2) можно применять и для стационарных детерминированных сигналов. Этим, априорно периодическим, сигналам соответствуют периодические авто­корреляционные функции (рисунок.5.3, в).

Если сигнал содержит как периодическую, детерминирован­ную, так и стохастическую составляющие, то в автокорреляцион­ной функции при больших 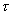стохастическая составляющая сигнала становится некоррелированной, соответствующая ей составляющая автокорреляционной функции исчезает и остается только периодическая составляющая, соответствующая детерминированной составляющей сигнала (рис.5.3, г). Корреляция в этом случае отображает эффект фильтрации, что может быть использовано в измерительной технике.

Контрольные вопросы: