Частотные характеристики апериодического сигнала

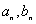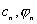Для апериодических сигналов так же, как и для периодических, расчетные методы, связанные с процессом передачи сигналов, значительно упрощаются при использовании их частотного пред­ставления. Однако для этих сигналов не могут быть использованы введенные выше коэффициенты Фурье или , так как «период» Т стремится к бесконечности.

Вместо ряда Фурье используют так называемое преобразование Фурье. Не давая здесь строго математической формулировки этого понятия, рассмотрим крат­ко его получение путем предельного перехода.

Вначале будем рассмат­ривать апериодический сиг­нал только на отрезке -T/2<t<T/2. Представим теперь периодический сигнал, который на указанном отрезке совпадает с первоначальным сигналом, а вне его периодически по­вторяется. Этот периодический сигнал можно представить в виде ряда Фурье

Если теперь указанный интервал (период) Т стре­мить к бесконечности, то соответствующий ряд Фурье будет описывать апериодический сигнал.

Как показано в предыдущей лекции, амплитудные и фазовые спектры рядов Фурье являются дискретными. Интервал между спектральными линиями равен

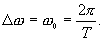
Если Т , будет стремиться к бесконечности, то спектральные линии станут все более и более сближаться, и при предельном переходе возникает непрерывный спектр. Однако одновременноисчезают коэффициенты Фурье, соответствующие отдельным амплитудам. Вместо них вводят так называемую плотность ампли­туды, например:

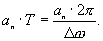
Таким образом, возникает непрерывно распределенная спек­тральная плотность амплитуды, которая не исчезает и при пре­дельном переходе.