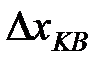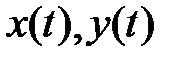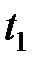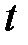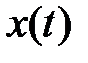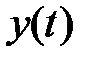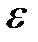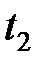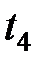Лекция 7 Дискретные сигналы Динамические погрешности измерения
Дискретизация или квантование величин производится любым экспериментатором при считывании результатов измерений со шкалы аналогового измерительного прибора. В цифровых измерительных приборах и в аналого-цифровых преобразователях дискретизация непрерывных величин производится автоматически. Квантование по уровню выполняется при численной регистрации любых экспериментальных данных. С математической точки зрения операция квантования связана с округлением значения непрерывной величины в соответствии с принятым правилом (например, отнесение к нижней,верхней границе интервала квантования или к его середине). Квантование по уровню приводит к появлению методической погрешности, которую ввиду ее случайного характера иногда называют шумом квантования. Строго говоря, погрешность дискретизации является неслучайной функцией неизвестного (случайного) значения измеряемой величины.
Наибольшее распространение на практике получило равномерное квантование по уровню, при котором диапазон возможных значений 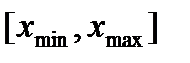 непрерывной величины
непрерывной величины 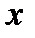 разбивается на
разбивается на 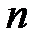 равных интервалов квантования
равных интервалов квантования
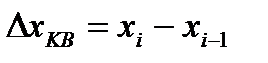 ,
, 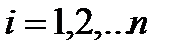 .
.
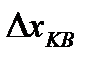 называется шагом квантования или шагом дискретизации. При равномерном квантовании
называется шагом квантования или шагом дискретизации. При равномерном квантовании 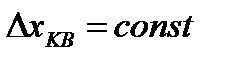 . В результате дискретизации значение
. В результате дискретизации значение 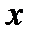 попадающее в интервал
попадающее в интервал 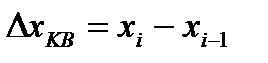 округляется до некоторой величины
округляется до некоторой величины 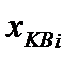 которая называется уровнем квантования. В качестве уровней квантования выбирают верхнюю или нижнюю границу интервалов квантования либо их середину. На рисунке7.1 уровнем квантования выбраны нижняя граница (а) или – середина (б). Очевидно, что в случае, изображенном на рис.7.1а, максимальное абсолютное значение погрешности квантования равно шагу квантования, а в случае, изображенном на рис.7.1б - половине шага квантования.Доказано, что при большом
которая называется уровнем квантования. В качестве уровней квантования выбирают верхнюю или нижнюю границу интервалов квантования либо их середину. На рисунке7.1 уровнем квантования выбраны нижняя граница (а) или – середина (б). Очевидно, что в случае, изображенном на рис.7.1а, максимальное абсолютное значение погрешности квантования равно шагу квантования, а в случае, изображенном на рис.7.1б - половине шага квантования.Доказано, что при большом 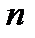 (
( 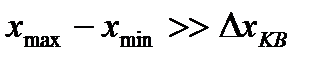 ) закон распределения погрешности квантования практически не зависит от закона распределения
) закон распределения погрешности квантования практически не зависит от закона распределения 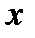 и близок к равномерному. Математические ожидания погрешности квантования в рассмотренных случаях различаются (причем на рис.7.1б математическое ожидание равно нулю), а дисперсии погрешности квантования в обоих случаях одинаковы и равны
и близок к равномерному. Математические ожидания погрешности квантования в рассмотренных случаях различаются (причем на рис.7.1б математическое ожидание равно нулю), а дисперсии погрешности квантования в обоих случаях одинаковы и равны 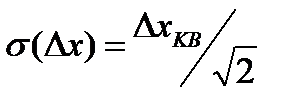 . Таким образом, в качестве уровней квантования целесообразно выбрать середины интервалов квантования и соответственно строить технические средства.
. Таким образом, в качестве уровней квантования целесообразно выбрать середины интервалов квантования и соответственно строить технические средства.
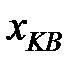
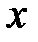
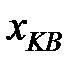
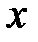
|
|
а б
Рисунок 7.1- Максимальное абсолютное значение погрешности квантования
Если закон распределения вероятностей значений измеряемой величины существенно отличается от равномерного, а число уровней квантования в диапазоне измерения невелико (меньше 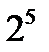 ), то может оказаться целесообразным неравномерное квантование по уровню, т. е. квантование с переменным шагом. На практике неравномерное квантование по уровню применяется весьма редко, например, в статистических анализаторах.
), то может оказаться целесообразным неравномерное квантование по уровню, т. е. квантование с переменным шагом. На практике неравномерное квантование по уровню применяется весьма редко, например, в статистических анализаторах.
Дискретизация по времени предполагает представление непрерывной функции 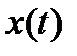 в виде дискретного набора значений
в виде дискретного набора значений 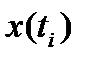 и, затем, ее восстановление. Простейший и наиболее распространенный способ временной дискретизации – выбор достаточно малого шага
и, затем, ее восстановление. Простейший и наиболее распространенный способ временной дискретизации – выбор достаточно малого шага 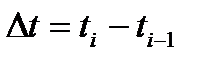 и соединение полученных точек прямыми линиями. При восстановлении непрерывной функции таким образом неизбежно возникают погрешности. Для уменьшения этих погрешностей необходимо уменьшить шаг квантования или, возможно, интерполировать функцию
и соединение полученных точек прямыми линиями. При восстановлении непрерывной функции таким образом неизбежно возникают погрешности. Для уменьшения этих погрешностей необходимо уменьшить шаг квантования или, возможно, интерполировать функцию 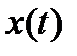 на каждом шаге дискретизации степенными многочленами. Современные электронные средства в большинстве случаев позволяют обеспечить достаточно малый шаг дискретизации при оцифровке сигналов, поэтому интерполяция многочленами используется только в особых случаях. Второй способ дискретизации по времени заключается в том, что непрерывная функция
на каждом шаге дискретизации степенными многочленами. Современные электронные средства в большинстве случаев позволяют обеспечить достаточно малый шаг дискретизации при оцифровке сигналов, поэтому интерполяция многочленами используется только в особых случаях. Второй способ дискретизации по времени заключается в том, что непрерывная функция 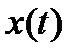 заменяется конечным числом коэффициентов разложения
заменяется конечным числом коэффициентов разложения 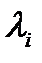 , по выбранной системе базисных функций
, по выбранной системе базисных функций 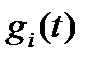 . В этом случае по каналу связи передаются только коэффициенты разложения, а восстановление исходной непрерывной функции осуществляется путем вычисления суммы
. В этом случае по каналу связи передаются только коэффициенты разложения, а восстановление исходной непрерывной функции осуществляется путем вычисления суммы 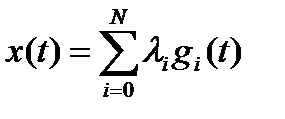 (7.1)
(7.1)
Наиболее широкое распространение разложение (7.1) получило для функции 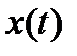 и базисных функций
и базисных функций 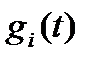 , удовлетворяющих теореме Котельникова.
, удовлетворяющих теореме Котельникова.
Пусть 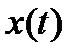 имеет ограниченный спектр, то есть ее преобразование Фурье
имеет ограниченный спектр, то есть ее преобразование Фурье 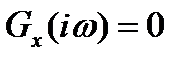 при
при 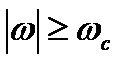 , где величина
, где величина 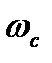 называется граничной частотой или частотой среза. Тогда, согласно теореме Котельникова, всегда можно выбрать интервал
называется граничной частотой или частотой среза. Тогда, согласно теореме Котельникова, всегда можно выбрать интервал 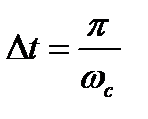 такой, что непрерывная функция может быть разложена в ряд
такой, что непрерывная функция может быть разложена в ряд
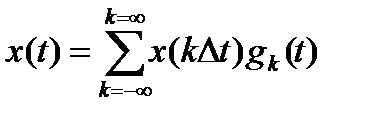 , ( 7.2)
, ( 7.2)
где
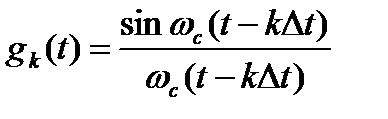 (7.3)
(7.3)
Таким образом, теоретически непрерывная функция 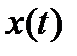 может быть точно восстановлена по дискретным отсчетам
может быть точно восстановлена по дискретным отсчетам 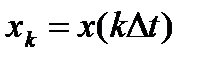 , и значениям базисной функции. При этом по каналам связи достаточно передавать дискретные отсчеты
, и значениям базисной функции. При этом по каналам связи достаточно передавать дискретные отсчеты 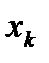 . Как уже отмечалось в предыдущем параграфе, в реальных условиях точное восстановление непрерывной функции невозможно из-за того, что не могут быть выполнены условия теоремы Котельникова. Реальные функции всегда существуют на конечных интервалах времени, поэтому их спектры не ограничены. Выбор частоты среза
. Как уже отмечалось в предыдущем параграфе, в реальных условиях точное восстановление непрерывной функции невозможно из-за того, что не могут быть выполнены условия теоремы Котельникова. Реальные функции всегда существуют на конечных интервалах времени, поэтому их спектры не ограничены. Выбор частоты среза 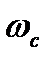 и соответствующего шага дискретизации
и соответствующего шага дискретизации 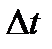 приводит к потере высокочастотных составляющих и появлению методической погрешности
приводит к потере высокочастотных составляющих и появлению методической погрешности 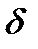 . За счет конечного времени определения функции (длительности
. За счет конечного времени определения функции (длительности 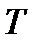 ), ее спектр ограничен и снизу – частотой
), ее спектр ограничен и снизу – частотой 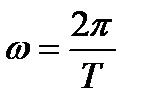 .
.
Дисперсия относительной погрешности из-за потери высокочастотных составляющих спектра определяется как отношение мощности сигнала в полосе частот 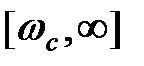 к мощности сигнала в полосе
к мощности сигнала в полосе 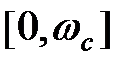 , т. е. к мощности той части спектра сигнала, которая может быть принципиально точно восстановлена:
, т. е. к мощности той части спектра сигнала, которая может быть принципиально точно восстановлена:
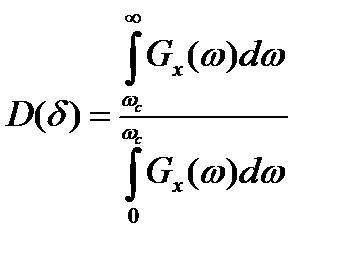 . (7.4)
. (7.4)
Адаптивная дискретизация. Пусть непрерывная функция 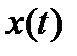 квантуется и затем восстанавливается по дискретным отсчетам. Если результат восстановления описывается функцией
квантуется и затем восстанавливается по дискретным отсчетам. Если результат восстановления описывается функцией 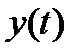 , то может быть выбран критерий точности восстановления
, то может быть выбран критерий точности восстановления 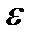 . Критерием может служить максимальное отклонение
. Критерием может служить максимальное отклонение
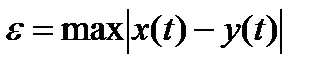 , (7.5)
, (7.5)
или среднеквадратичное отклонение
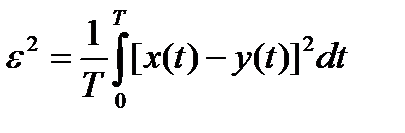 , (7.6)
, (7.6)
где 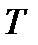 - интервал аппроксимации. Если дискретные по времени отсчеты непрерывной функции используются в дальнейшем для восстановления этой
- интервал аппроксимации. Если дискретные по времени отсчеты непрерывной функции используются в дальнейшем для восстановления этой
-
|
|
|
|
|
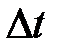
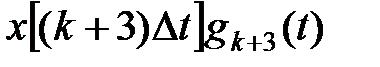
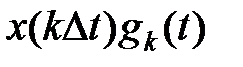
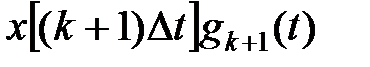
Рисунок 7.2-Процесс дискретизации и квантования сигнала
функции, то очевидно, что при заданном шаге дискретизации погрешность восстановления функции будет зависеть от способа ее восстановления (приближения). И, наоборот, при заданной допустимой погрешности восстановления способ приближения функции будет определять максимальное значение шага дискретизации. В связи с этим задача дискретизации может быть сформулирована следующим образом: имеется непрерывная функции, требуется определить интервалы квантования по времени, при которых отклонение между исходной и восстановленной функциями не превышало бы заданного значения. При равномерной дискретизации отклонение, в зависимости от поведения исходной функции, будет достигать допустимого значения только в отдельные интервалы времени. В остальное время погрешность будет меньше допустимой, а шаг квантования теоретически может быть на отдельных временных участках увеличен (уменьшено общее количество отсчетов). Таким образом, осуществляется адаптивная дискретизация, позволяющая, оптимизировать количество точек квантования в зависимости от конкретного поведения исходной функции
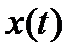 .
.
|
|
|
|
|
|
|
|
|
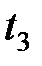
Идея адаптивной дискретизации состоит в следующем. На основе имеющегося дискретного отсчета (или отсчетов) на текущем интервале дискретизации определяются параметры воспроизводящей функции. Затем в любой текущий момент времени находится разность между соответствующими значениями исходной и воспроизводящей функций, т.е. погрешность воспроизведения . Если эта погрешность достигает предельно допустимого значения, то фиксируется конец интервала дискретизации, т. е. осуществляется новый отсчет. При этом восстановление непрерывной функции осуществляется чаще всего степенными полиномами. Возможен и другой подход к адаптивной дискретизации, заключающийся в адаптивном изменении порядка приближающего полинома при фиксированном интервале дискретизации. Однако на практике наибольшее распространение получила адаптивная дискретизация с переменным шагом квантования.
|
|
|
|
|
|
|
|
|
|
Рисунок 7.3 - Адаптивная дискретизация
с р адаптивной дискретизации с восстанавливающей функцией вида
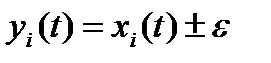 .
.
На Рисунке 7.2 показан пример адаптивной дискретизации с использованием линейной экстраполяции (полиномом первого порядка):
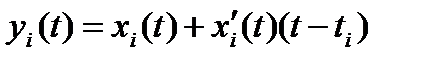 .
.
Как видно из рисунков 7.2-7.3, количество отсчетов при адаптивной дискретизации сильно зависит от конкретного вида функции (ступенчатая функция требует трех отсчетов, а линейная экстраполяция - четырех). Поэтому адаптивная дискретизация достаточно редко используется для сигналов, форма которых заранее известна. При современном уровне цифровой электронной техники в большинстве практически важных случаев оказывается проще для получения необходимой точности увеличить частоту равномерной дискретизации.
Общая схема цифровых измерительных приборов. В цифровых измерительных приборах (ЦИП) обязательно выполняются следующие операции: квантование измеряемой величины по уровню, ее дискретизация по времени и кодирование, т.е. преобразование в цифровой код. Большинство современных ЦИП имеют выход, позволяющий передавать измерительную информацию в компьютер, и одна из их важнейших функций – использование в качестве промежуточных измерительных преобразователей аналоговых величин в цифровой код в информационно-измерительных и автоматизированных системах контроля и управления с цифровой обработкой
АП преобразует измеряемую величину 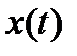 в функционально с ней связанную аналоговую величину
в функционально с ней связанную аналоговую величину 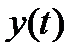 , более удобную для преобразования в цифровой код. В качестве АП используются усилители, делители, фильтры, преобразователи неэлектрических величин в электрические и т. п.. АП является важнейшим элементом измерительного прибора, поскольку именно он определяет чувствительность, динамический диапазон и частотный диапазон прибора.
, более удобную для преобразования в цифровой код. В качестве АП используются усилители, делители, фильтры, преобразователи неэлектрических величин в электрические и т. п.. АП является важнейшим элементом измерительного прибора, поскольку именно он определяет чувствительность, динамический диапазон и частотный диапазон прибора.
Аналого-цифровой преобразователь выполняет операции квантования по уровню и по времени аналоговой величины, сравнения ее с мерой и кодирование результатов. При этом на выходе вырабатывается дискретный сигнал ДС, который преобразуется ЦС в цифровой отсчет 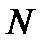 или в виде кода вводится в компьютер.
или в виде кода вводится в компьютер.
Образцовой мерой может служить, например, генератор импульсов с эталонной амплитудой и частотой повторения.
Цифровым средством отображения информации служит обычно цифровой индикатор или дисплей. В качестве устройства управления можно использовать микропроцессор, который реализует необходимый алгоритм измерения
Статическая и динамическая погрешности.Статическая погрешность измерений - погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.
Динамическая погрешность измерений - погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Контрольные вопросы
1. Как осуществляется дискретизация сигналов по уровню и времени?
2. Теорема Котельникова.
3. Идея адаптивной дискретизации.
Лекция Случайные величины в статистической радиотехнике. Основные понятия теории вероятности Случайная величина. Основные теоремы теории вероятности. Случайные величины и их законы распределения
Основным типом погрешностей, изучению которых посвящено последующее изложение, являются случайные погрешности. Они поддаются строгому математическому описанию, что позволяет делать выводы о качестве измерений, в которых они присутствуют. Погрешности других типов более сложны для анализа, их выявляют и анализируют только в условиях конкретного эксперимента. Чтобы знать, как надлежит работать со случайными погрешностями, рассмотрим приемы статистического описания случайных величин. Начнем с предполагаемого эксперимента, в котором выполняют многократные прямые измерения какой-то случайной физической величины, проводимые без изменения условий эксперимента. Закономерности в поведении величины видны из гистограммы. Гистограмма – ступенчатая диаграмма, показывающая , как часто при измерениях появляются результаты, попадающие в тот или иной интервал Dxмежду наименьшим xmin и наибольшим xmaxиз измеренных значений величины x. Гистограмму строят в следующих координатах: по оси абсцисс откладывают измеряемую величину x, по оси ординат – Dn/nDx (рис.3.1). Здесь n – полное количество проведенных измерений, Dn – количество результатов, попавших в интервал [x, x+Dx] .
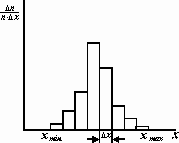
Рисунок.8.1- Гистограмма.
Отношение Dn/nесть доля результатов, оказавшихся в указанном интервале. Оно имеет смысл вероятности попадания результата отдельного измерения в данный интервал. Выражение Dn/(n-Dx), получаемое после деления Dn/n на ширину интервала Dx, приобретает смысл плотности вероятности.
При очень большом количестве измерений (n 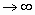 ) весь диапазон изменения величины x можно разбить на бесконечно малые интервалы dx , как это делается в математике, и найти количество результатов dn в каждом из них. В этом случае гистограмма превратится в плавную кривую – график функции
) весь диапазон изменения величины x можно разбить на бесконечно малые интервалы dx , как это делается в математике, и найти количество результатов dn в каждом из них. В этом случае гистограмма превратится в плавную кривую – график функции

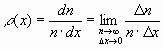 . (8.1)
. (8.1)
Такую функцию называют плотностью вероятности, или распределениемвероятности, иногда – просто распределением величины x. Примеры конкретных распределений можно найти на рис.8.2.
Распределение выступает в роли исчерпывающей характеристики случайной величины. Закон распределения можно задать в виде функционального выражения, графика, таблицы или каким-то другим способом. При любом варианте задания устанавливается связь между вероятностью того, что результат однократного измерения случайной величины попадет в заданный интервал возможных значений, и шириной этого интервала.
Распределение содержит наиболее полную информацию о случайной величине, однако пользоваться им не всегда удобно. Оперируя результатами проведенного эксперимента, вместо функции распределения лучше иметь привычные числовые величины, ими являются - среднее значениеи дисперсия.
Среднее значение 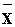 измеряемой величины x указывает центр распределения, около которого группируются результаты отдельных измерений
измеряемой величины x указывает центр распределения, около которого группируются результаты отдельных измерений
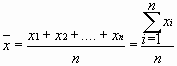 . (8.2)
. (8.2)
Дисперсиювводят как средний квадрат отклонения отдельных результатов от среднего значения случайной величины
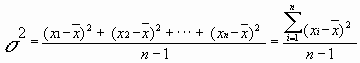 (8.3)
(8.3)
Среднее квадратичное отклонение, называемое также стандартным, определяют как квадратный корень из дисперсии
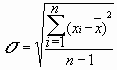 . (8.4)
. (8.4)
Как следует из способа вычисления , эта величина характеризует разброс результатов отдельных измерений вокруг среднего значения, получаемого после обработки всех данных многократного измерения. Конечно, точные значения 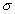 и
и 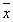 являются предельными величинами, так как могут быть получены лишь тогда, когда полное количество проведенных измерений достаточно велико, в пределе при
являются предельными величинами, так как могут быть получены лишь тогда, когда полное количество проведенных измерений достаточно велико, в пределе при 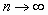 . При конечных n правильнее использовать терминэкспериментальная оценка, который в равной мере относится и к среднему значению, и к дисперсии. Обратим внимание на знаменатель выражений (8.3) и (8.4), который превращается в нуль при n=1. Насколько это правильно? Ведь в этом случае, казалось бы, s2 и s становятся бесконечно большими. Обратимся к реальной ситуации, соответствующей n=1, т.е. к эксперименту, в котором выполнено только одно измерение x1 величины x. Его недостаточно, чтобы построить гистограмму и найти из нее s2 . Значит, s2 и sоказываются полностью неопределенными вследствие недостаточности экспериментальной информации. Выражения (8.2) – (8.4) учитывают приведенные соображения: если n=1 , из (8.2) получается
. При конечных n правильнее использовать терминэкспериментальная оценка, который в равной мере относится и к среднему значению, и к дисперсии. Обратим внимание на знаменатель выражений (8.3) и (8.4), который превращается в нуль при n=1. Насколько это правильно? Ведь в этом случае, казалось бы, s2 и s становятся бесконечно большими. Обратимся к реальной ситуации, соответствующей n=1, т.е. к эксперименту, в котором выполнено только одно измерение x1 величины x. Его недостаточно, чтобы построить гистограмму и найти из нее s2 . Значит, s2 и sоказываются полностью неопределенными вследствие недостаточности экспериментальной информации. Выражения (8.2) – (8.4) учитывают приведенные соображения: если n=1 , из (8.2) получается 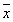 и, как следствие, числитель, и знаменатель в (8.3) и (8.4) одновременно обращаются в нуль. Это свидетельствует об ожидаемой неопределенности значения x. Строгое обоснование справедливости приведенных выражений делается в математической статистике. Отметим, что среднее значение случайной величины нельзя расценивать как однозначный результат измерения. Иначе надо было бы полагать, что случайная величина всегда имеет только одно постоянное значение , чего не может быть в действительности из-за ее случайной природы. Случайные факторы, характеризующие форму распределения случайной величины, не связаны только с возможной неточностью измерительных приборов, а значит, среднее квадратичное отклонение s, описывающее форму распределения, объективно отражает характер поведения исследуемой случайной величины.
и, как следствие, числитель, и знаменатель в (8.3) и (8.4) одновременно обращаются в нуль. Это свидетельствует об ожидаемой неопределенности значения x. Строгое обоснование справедливости приведенных выражений делается в математической статистике. Отметим, что среднее значение случайной величины нельзя расценивать как однозначный результат измерения. Иначе надо было бы полагать, что случайная величина всегда имеет только одно постоянное значение , чего не может быть в действительности из-за ее случайной природы. Случайные факторы, характеризующие форму распределения случайной величины, не связаны только с возможной неточностью измерительных приборов, а значит, среднее квадратичное отклонение s, описывающее форму распределения, объективно отражает характер поведения исследуемой случайной величины.
Если, помимо характерных для распределения значений величин 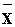 и s, известен функциональный вид распределения случайной величины, то можно получить полную информацию о вероятности реализации случайной величины в любом заданном интервале значений. Рассмотрим это на примере нормального, или Гауссова, распределения, отображающего ситуацию, наиболее часто встречающуюся в природе. Как следствие, ему присуща особая роль, объясняемая тем, что при обработке данных измерений в науке и технике обычно предполагают нормальный закон распределения случайных погрешностей измерений. В пользу применения нормального распределения имеются веские основания. А именно, оно всегда проявляется тогда, когда суммарная погрешность есть результат неучтенного совместного воздействия целого ряда причин, каждая из которых дает малый вклад в погрешность.
и s, известен функциональный вид распределения случайной величины, то можно получить полную информацию о вероятности реализации случайной величины в любом заданном интервале значений. Рассмотрим это на примере нормального, или Гауссова, распределения, отображающего ситуацию, наиболее часто встречающуюся в природе. Как следствие, ему присуща особая роль, объясняемая тем, что при обработке данных измерений в науке и технике обычно предполагают нормальный закон распределения случайных погрешностей измерений. В пользу применения нормального распределения имеются веские основания. А именно, оно всегда проявляется тогда, когда суммарная погрешность есть результат неучтенного совместного воздействия целого ряда причин, каждая из которых дает малый вклад в погрешность.
Нормально распределенная случайная величина имеет следующие свойства:
1. Она может принимать непрерывный ряд значений от – ? до + ?.
2. Центр распределения случайной величины одновременно является центром симметрии, т.е. одинаковые отклонения результатов измерения в меньшую и в большую стороны от центра встречаются одинаково часто.
3. Малые отклонения встречаются чаще больших, другими словами, реализуются с большей вероятностью.
Соответствующее функциональное выражение для распределения задает формула Гаусса
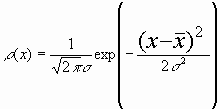 , (8.5)
, (8.5)
где 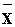 и s соответствуют использованным в (3.2) – (3.4), выражение exp(y) = e y – экспонента, в которой e = 2,71828 – основание натуральных логарифмов. Кривые нормального распределения для трех значений s (1; 0,5 и 0,25) и одинакового
и s соответствуют использованным в (3.2) – (3.4), выражение exp(y) = e y – экспонента, в которой e = 2,71828 – основание натуральных логарифмов. Кривые нормального распределения для трех значений s (1; 0,5 и 0,25) и одинакового 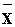 =3 приведены на рис.3.2.
=3 приведены на рис.3.2.
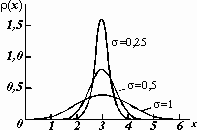
Рисунок 8.2- Нормальное распределение для = 3; s = 0,25; 0,5 и 1.
Распределение, задаваемое функцией Гаусса, симметрично относительно максимума, находящегося при
x = 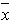 . Значение функции в максимуме
. Значение функции в максимуме
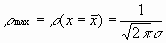 . (8.6)
. (8.6)
Значение аргумента x, при котором плотность вероятности максимальна, является наиболее вероятным при реализации случайной величины. Следовательно, 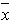 – оценка наиболее вероятного значения случайной величины, распределенной по нормальному закону. Согласно (3.6) значение функции Гаусса в максимуме уменьшается с увеличением s. Одновременно кривые на графике становятся более пологими, но полная площадь под кривой остается при этом неизменной.
– оценка наиболее вероятного значения случайной величины, распределенной по нормальному закону. Согласно (3.6) значение функции Гаусса в максимуме уменьшается с увеличением s. Одновременно кривые на графике становятся более пологими, но полная площадь под кривой остается при этом неизменной.
Воспользуемся выражением (8.1) и получим из него 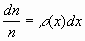
Это соотношение означает, что вероятность попадания результата отдельного измерения в бесконечно малый промежуток dx равна площади под кривой распределения на этом промежутке. Если расширить промежуток до конечной величины [x1, x2], то площадь под кривой даст вероятность P попадания результата измерения уже в конечный промежуток. Вероятность, как площадь, математически выражается интегралом
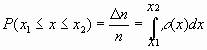 . (8.7)
. (8.7)
В скобках после P указано событие, для которого вычислена вероятность. При раздвигании границ промежутка в обе стороны до бесконечности интеграл от функции распределения 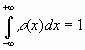
Смысл этого равенства заключается в том, что вероятность достоверного события равна единице. Достоверным событием в рассматриваемой ситуации является реализация какого-то значения случайной величины (от –? до +?) в результате ее однократного измерения. Интегралы от функции Гаусса для различных пределов интегрирования вычислены и заданы в виде подробных таблиц. Для проведения анализа распределения обычно используют симметричный относительно интервал 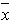 -Dx,
-Dx, 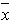 +Dx , где Dx– произвольное отклонение от среднего, интервал введен через e – величину отношения полуширины интервала Dx к среднему квадратичному отклонению s:
+Dx , где Dx– произвольное отклонение от среднего, интервал введен через e – величину отношения полуширины интервала Dx к среднему квадратичному отклонению s: 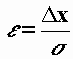 . (8.8)
. (8.8)
Задана вероятность a
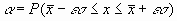 . (8.9)
. (8.9)
Ее можно рассчитать по приближенному выражению, полученному из (8.7):
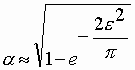 ( 8.10)
( 8.10)
Однако проще запомнить несколько полезных цифр.
| При e = 1 | a = 0,68 (или 68%). |
| При e = 2 | a = 0,95 (или 95%). |
| При e = 3 | a = 0,997 (или 99,7%). |
Смысл соотношений (8.10) заключается в установлении связи между шириной интервала ± Dx вокруг и вероятностью попадания измеренного значения случайной величины в этот интервал, если величина распределена по нормальному закону. Так, результат измерения с вероятностью 68% попадет в интервал [– s, + s], т.е. примерно каждое третье измерение даст результат за пределами этого интервала. За пределами интервала [-2s, +2s] окажется один результат из двадцати, а для интервала -3s, +3s – только один из трехсот. Значит, интервал ±3s вокруг является почти достоверным, так как подавляющее большинство отдельных результатов многократного измерения случайной величины окажется сосредоточенным именно в нем. Опережая ход изложения, заметим, что часто используемое при измерениях правило 3s, или правило трех стандартов, основано на указанном свойстве нормального распределения. С учетом проведенного выше анализа, можно установить наличие промаха в результате отдельного измерения, а значит, отбросить его, если результат измерения более чем на 3s отличается от измеренного среднего значения случайной величины.
Дата добавления: 2015-12-11; просмотров: 3047;