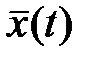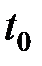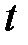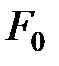Характеристики случайного процесса
Случайные динамические процессы. Пусть случайная функция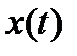 
характеризуется функцией распределения вероятностей 
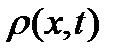. Функция 
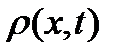определяет вероятность принятия различных значений 
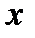в фиксированные моменты времени.
Вероятность для 
принять в момент времени 
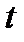значение в некотором интервале 
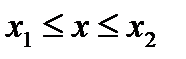записывается в виде:
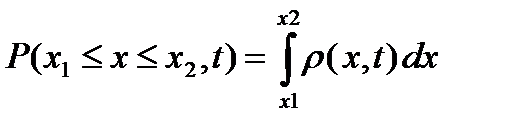. (8.11)
С вероятностью равной единице, находится на интервале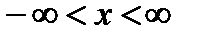 
. Т.е. функция 
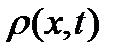должна удовлетворять условию нормировки:
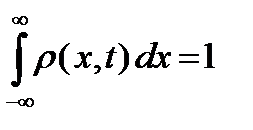
Если рассмотреть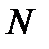 
дискретных реализаций процесса 
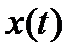, то
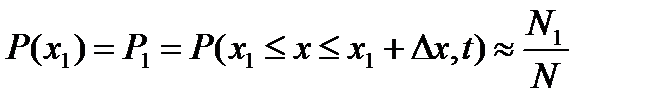, (8.12)
где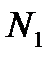 
– число реализаций, когда значение 
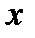в момент 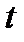находится в интервале 
.
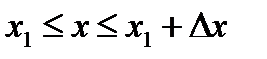Статистическое описание процесса возможно при условии, что отношение 
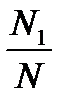устойчиво , т.е.
при 
. (8.13)
При малом 
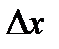из (8.1.1) следует
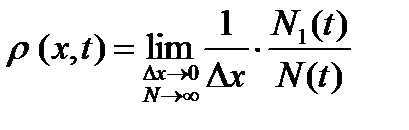. (8.14)
Учитывая (8.11-8.14) можно показать, что среднее (по реализациям случайного процесса) значение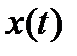 
вычисляется по традиционной формуле в каждый момент времени:
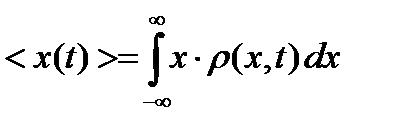. (8.15)
Если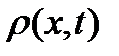 
не зависит от 
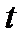, т.е. 
, то процесс называется стационарным. В дальнейшем мы ограничимся рассмотрением таких процессов.
Для вычисления среднего значения случайной функции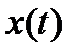 
по каждой реализации (среднее по времени) необходимо выбрать только временной интервал усреднения 
:
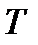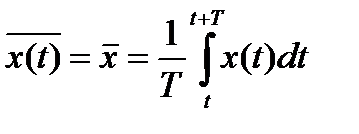. (8.16)
В том случае, если анализируется распределение функции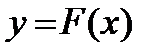 
, то её среднее значение вычисляется в виде
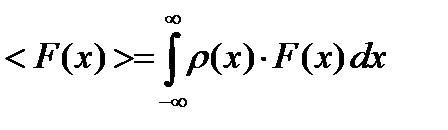. (8.17)
Аналогично записываются выражения для различных средних:
моменты случайного процесса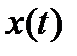
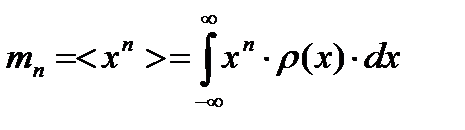; (8.18)
центральные моменты:
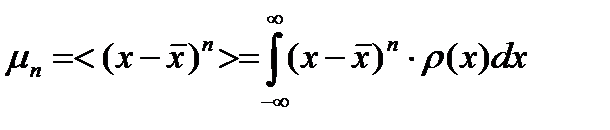. (8.19)
Пусть необходимо найти распределение функции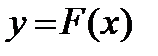 
. Если функция однозначна, то можно построить обратную функцию 
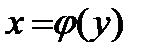. Зная распределение 
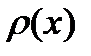найдем распределение 
.
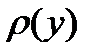Если в интервале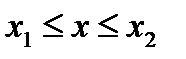 
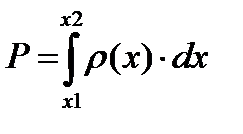, (8.20)
то перейдя к переменной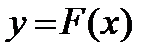 
, мы получим
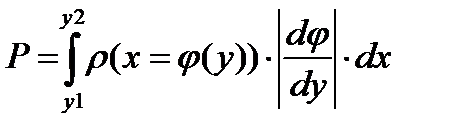. (8.21)
Из (5.1.11) следует, что
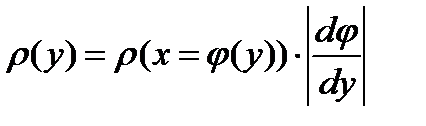. (8.22)
Формула (5.1.12) справедлива для любой однозначной функциональной зависимости от случайной переменной и может использоваться на практике.
Если зависимость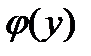 
многозначна и имеет несколько ветвей 
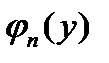, то
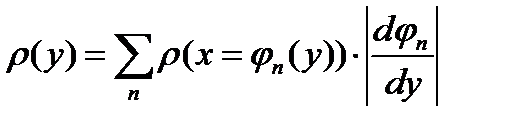. (8.23)
Корреляционные и спектральные характеристики случайного процесса. Случайный процесс называется эргодическим (эргодичным), если для него усредненное значение по времени равно усредненному значению по реализации, т.е.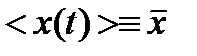 
при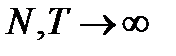 
. Рассмотрим далее временные характеристики таких процессов.
Пусть имеется две случайных функции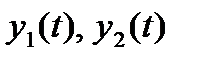 
. Взаимная корреляционная функция этих случайных процессов рассчитывается в виде
Нормируя корреляционную функция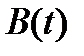 
получим коэффициент корреляции
,
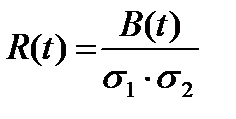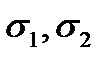- дисперсии случайных процессов 
, 
.
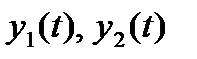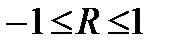Если 
и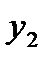 
– значения одного и того же случайного процесса 
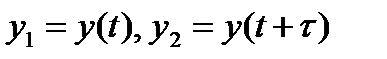, то можно рассчитать коэффициент автокорреляции
.
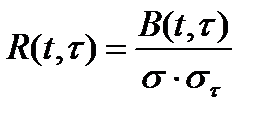Если процесс стационарен, то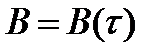 
, т.е. функция автокорреляции зависит только от временного сдвига 
и не зависит от времени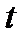 
. Иногда это утверждение считается определением стационарного процесса.
Кроме того, для стационарного случайного процесса функция автокорреляции симметрична, т.е.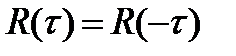 
.
Из сказанного выше следует:
.
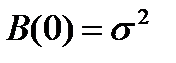Характерный интервал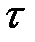 
, на котором функция автокорреляции 
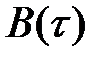уменьшается в 
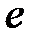раз, называется временем корреляции. Время корреляции определяет, насколько в случайном процессе каждое следующее во времени его значение связано с предыдущим.
Спектральное представление случайного процесса. Запишем флуктуационную составляющую случайного процесса
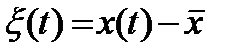, (8.24)
и представим ее в виде интеграла Фурье:
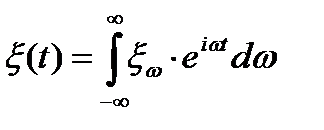. (8.25)
Спектральная амплитуда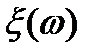 
является случайной функцией частоты 
.
Для вещественной функции 
спектральная амплитуда комплексна и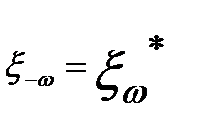 
, где «*» означает комплексное сопряжение.
Спектральной плотностью случайного процесса по определению называется величина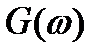 
, такая, что 
.
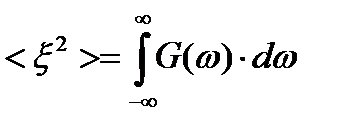Для стационарных случайных процессов характерно следующее важнейшее свойство: спектральная плотность процесса является Фурье-преобразованием от автокорреляционной функции (теорема Винера-Хинчина):
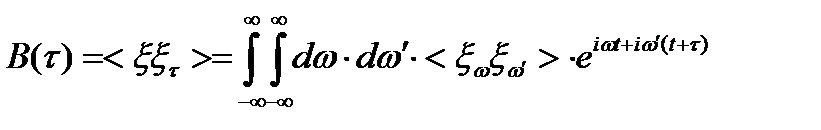(8.26)
для стационарного процесса должна отсутствовать зависимость от 
. Это возможно лишь в том случае, если спектральные амплитуды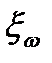 
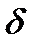-коррелированны и
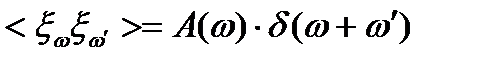. (8.27)
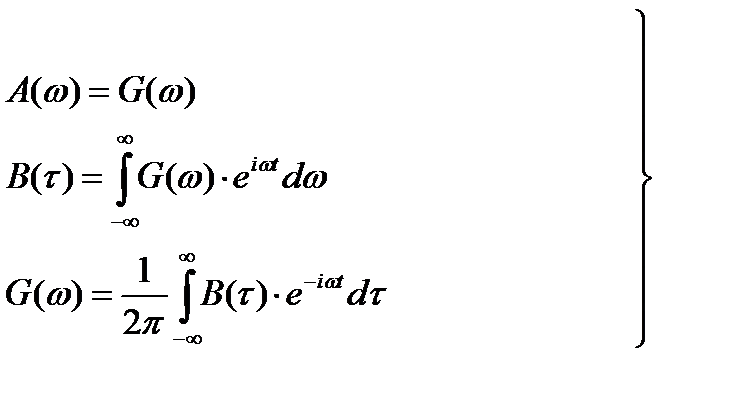. (8.28)
Из (8.28) следует, что если обозначить ширину спектра случайного процесса 
, то
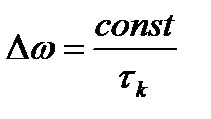, (8.29)
где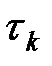 
- характерное время корреляции.
Здесь показана реализация процесса (рис.8.3,а) и эта же реализация, подвергнутая сглаживанию методом скользящего среднего, ее статистическому распределению, и автокорреляционной функции. Процесс имеет распределение, близкое к нормальному (гистограмма на рис.8.3,а, зависимость 2) и, практически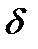 
-коррелирован, то есть имеет время корреляции 
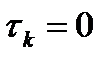и широкий спектр (автокорреляционная функция на рис.8.3,а, зависимость 3). После сглаживания статистическое распределение практически не меняется, но время корреляции увеличивается, т.е. происходит высокочастотная фильтрация.
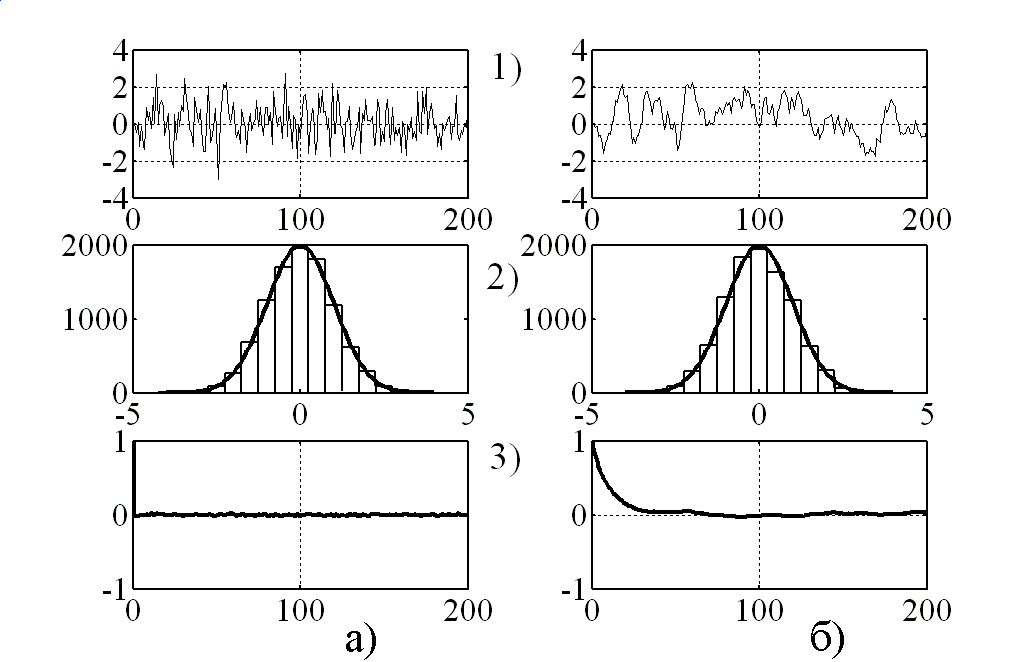
Рисунок 8.3- реализация процесса, подвергнутая сглаживанию методом скользящего среднего, и автокорреляционной функции.
Рассмотрим несколько моделей случайных импульсных процессов:
Одиночный случайный импульс
Пусть форма импульса известна и задается функцией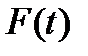 
, а момент его появления случаен и меняется от реализации к реализации:
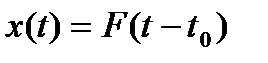. (8.31)
Импульс со случайной структурой описывается в виде:
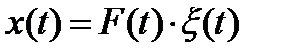, (8.32)
где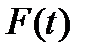 
- регулярная функция (огибающая импульса)
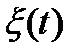- случайный процесс (функция может быть комплексной).
1. Случайная импульсная последовательность
В этом случае процесс состоит из совокупности импульсов
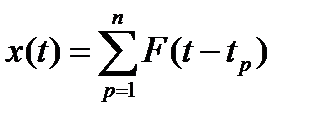, (8.33)
где 
- регулярная функция, описывающая форму импульса;
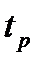может быть случайным моментом появления каждого импульса. Случайным может быть и число 
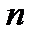- количество импульсов.
2. Квазипериодический импульсный процесс.
В этом случае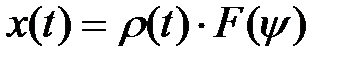 
, (8.34)
где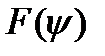 
- периодическая функция, удовлетворяющая следующему условию:
Аргумент этой функции следующим образом зависит от времени:
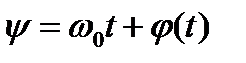. (8.35)
Если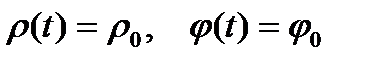 
, то выражение (8.34) определяет регулярную периодическую последовательность импульса произвольной формы 
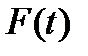. При случайных 
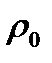и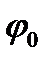 
выражение (8.34) определяет последовательность импульса со случайной амплитудой и длительностью.
Рассмотрим статистические характеристики таких импульсных процессов на примере одиночного случайного импульса.
Одиночный случайный импульс. Для одиночного случайного импульса средние значения и корреляционная функция описываются следующим образом:
, (8.36)
где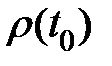 
- распределение вероятности случайного момента 
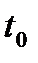появления импульса.
Пусть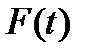 
имеет максимум в точке 
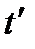, а «длительность» распределения 
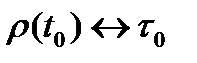, максимум 
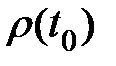соответствует моменту времени 
', 
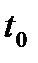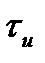- длительность импульса 
.
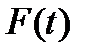Согласно (8.36) в предельных случаях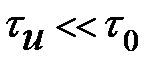 
и 
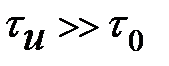выражение для 
будет иметь вид:
при 
; (8.37)
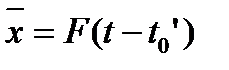при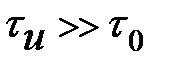 
. (8.38)
Аналогичным образом упрощаются выражения для корреляционной функции:
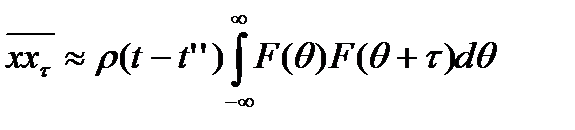, (8.39)
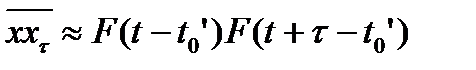. (8.40)
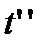определяется из условия, когда 
принимает максимальное значение.
Таким образом, одиночный импульс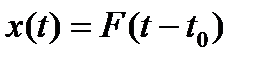 
при случайном 
не является стационарным случайным процессом, т.к. среднее значение и автокорреляционная функция зависят от времени.
Получим среднее значение импульса гауссовой формы при гауссовом распределении 
.
Т.е.
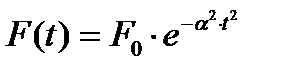, (8.41)
а
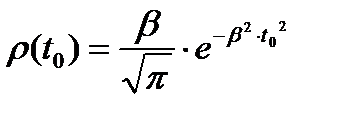. (8.42)
Здесь 
, 
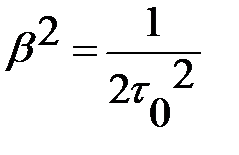. Используя (8.41) и (8.42) в (8.36) получим
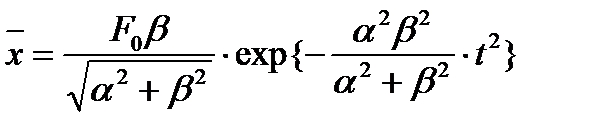. (8.43)
Проанализируем (8.43). Пусть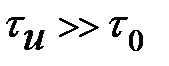 
, тогда 
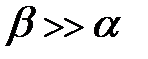и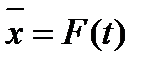 
, что согласуется с (8.38). Если 
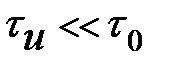то
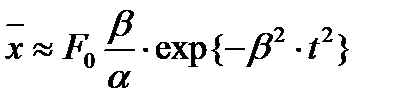. (8.44)
Соответствующее временное поведение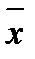 
показано на рис.5.3.
Условие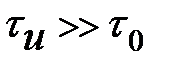 
означает, что временное положение импульса мало меняется от реализации к реализации и величина 
принимает форму единичного импульса (сплошная кривая на рис.8.4). При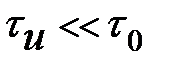 
импульс «растекается» в пределах временного интервала и его среднее значение имеет меньшую амплитуду и большую длительность (прерывистая линия )
|
|
|
|
Рисунок 8.4- среднее значение импульса гауссовой формы при гауссовом распределении .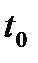
Пусть появление импульса равновероятно для любого момента на достаточно большом интервале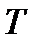 
:
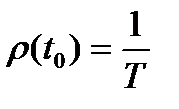при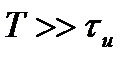 
.
Тогда среднее значение и корреляционная функция перестают зависеть от времени.
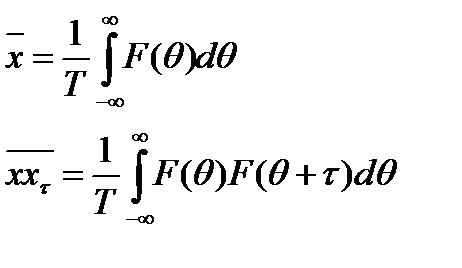. (8.45)
Таким образом, процесс становится стационарным в пределах интервала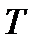 
.
Контрольные вопросы
1 Корреляционные и спектральные характеристики случайного процесса.
2 Что определяет среднее значение и дисперсия?
3 В чем физический смысл определения плотности вероятности?
4 Понятие случайных динамических процессов.
5 Какой процесс называется эргодическим?
Дата добавления: 2015-12-11; просмотров: 1209;