Линейная регрессия Подбор эмпирических формул Погрешности метода наименьших квадратов
Этот метод является одним из наиболее распространенных приемов статистической обработки экспериментальных данных, относящихся к различным функциональным зависимостям физических величин друг от друга. В том числе, он применим к линейной зависимости, и позволяет получить достоверные оценки ее параметров a и b, а также оценить их погрешности. Подробно он был рассмотрен в 4 лекции. Рассмотрим статистическую модель эксперимента, в котором исследуют линейную зависимость. Пусть проведено n парных измерений величин x и y: xi, yi, где i = 1, ... , n. По экспериментальным данным необходимо найти оценки параметров a и b, а также оценки их дисперсий sa2 и sb2. О природе экспериментальных погрешностей сделаем следующие предположения.
1. Значения xi известны точно, т.е. без погрешностей.
Конечно, в реальном эксперименте такое предположение вряд ли выполнено. Скорее всего, погрешности Dxi распределены нормально и могут быть пересчитаны в погрешности Dyi . Это вызовет увеличение дисперсии s2 распределения величин yi, что должно учитываться в процессе обработки данных методом наименьших квадратов.
2 Распределения величин yi взаимно независимы, имеют одну и ту же дисперсию s2 и отвечают нормальному закону. Распределения yi имеют средние значения 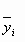 , которые совпадают с точным значением функции axi+b.
, которые совпадают с точным значением функции axi+b.
Это предположение иллюстрирует рисунке10.1

Рисунок 10.1- Иллюстрация модели метода наименьших квадратов.
Рассмотрим один из методов, позволяющих проанализировать и обработать данные, полученные в результате эксперимента (таблица 10.1). Пусть в результате измерений получена таблица зависимости одной величины 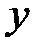 от другой
от другой 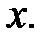
Таблица 10.1
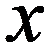
|
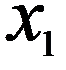
|
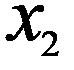
|

|
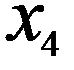
| ... |
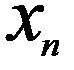
|
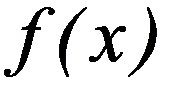
|
|

|
|
| ... |
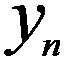
|
Необходимо найти формулу 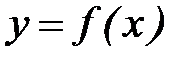 , выражающую таблично заданную зависимость аналитически. Применение интерполяции в данном случае нецелесообразно, т.к. значения
, выражающую таблично заданную зависимость аналитически. Применение интерполяции в данном случае нецелесообразно, т.к. значения 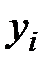 в узлах получены экспериментально и поэтому являются сомнительными (в ходе эксперимента возникает неустранимая погрешность, обусловленная неточностью измерений). Кроме того, совпадение значений в узлах не означает совпадения характеров поведения исходной и интерполирующей функции. Поэтому необходимо найти такой метод подбора эмпирической формулы, который не только позволяет найти саму формулу, но и оценить погрешность подгонки.
в узлах получены экспериментально и поэтому являются сомнительными (в ходе эксперимента возникает неустранимая погрешность, обусловленная неточностью измерений). Кроме того, совпадение значений в узлах не означает совпадения характеров поведения исходной и интерполирующей функции. Поэтому необходимо найти такой метод подбора эмпирической формулы, который не только позволяет найти саму формулу, но и оценить погрешность подгонки.
Постановка задачи. Найдем функцию заданного вида
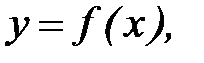 (10.1)
(10.1)
которая в точках 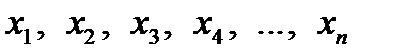 принимает значения как можно более близкие к табличным значениям
принимает значения как можно более близкие к табличным значениям  .
.
Практически вид приближающей функции можно определить визуально: по таблице 10.1 строится точечный график функции, а затем проводится кривая, по возможности наилучшим образом отражающая характер расположения точек (рис.10.1).
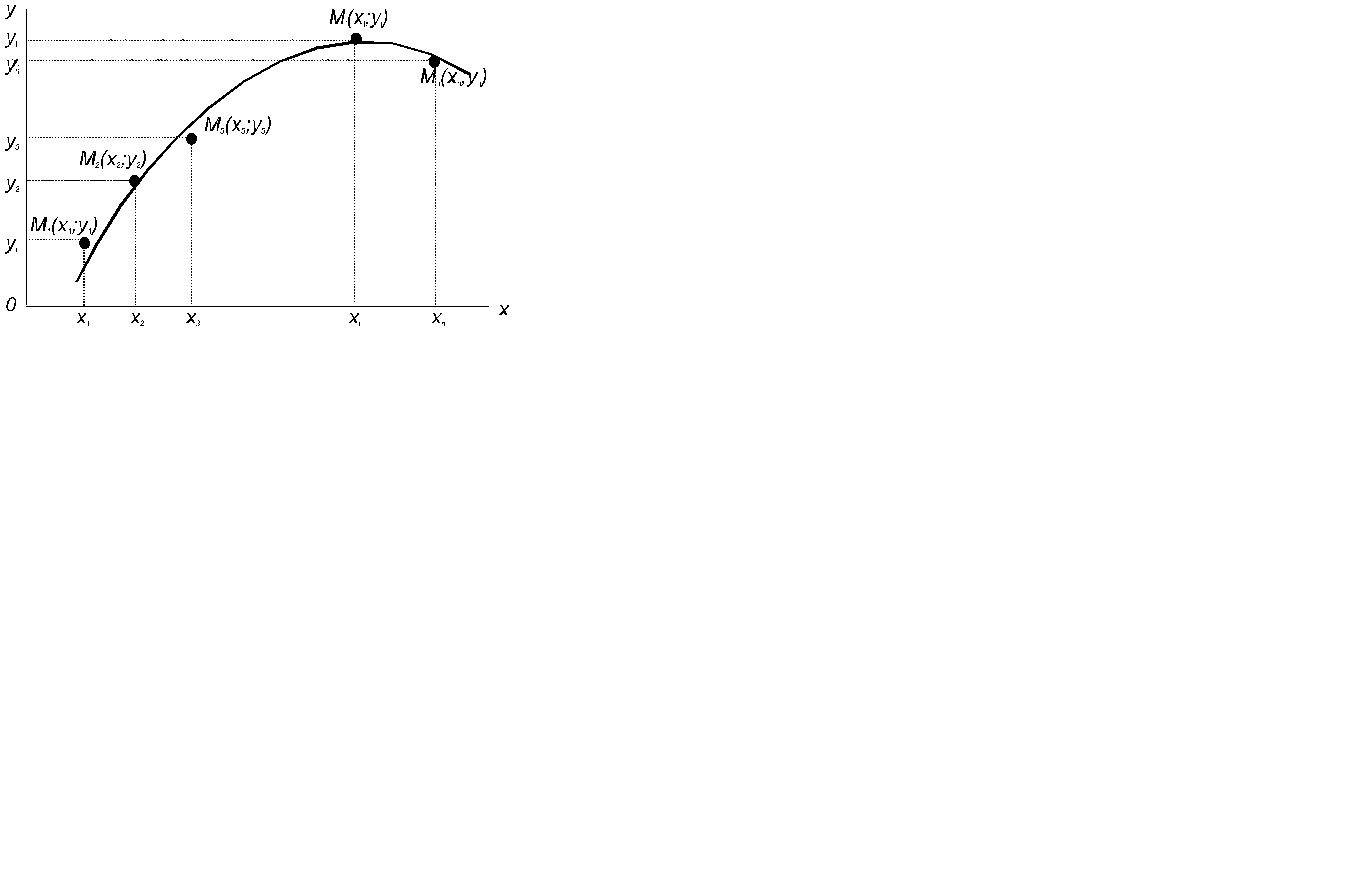
Рисунок.10.1- Точечный график функции
По полученной кривой устанавливается вид приближающей функции (обычно из числа простых по виду аналитических функций: линейная, степенная, экспоненциальная логарифмическая, гипербола, и т.д.).
Заметим, что формула (10.1), называемая эмпирической формулой или уравнением регрессии 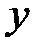 на
на  , позволяет находить значения функции
, позволяет находить значения функции 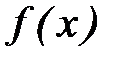 для нетабличных значений
для нетабличных значений  , «сглаживая» результаты измерений величины
, «сглаживая» результаты измерений величины 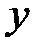 .
.
Из рисунка 10.1 видно, что для каждого значения  экспериментальное
экспериментальное 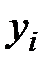 и расчетное
и расчетное 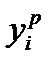 значения различаются на некоторую величину
значения различаются на некоторую величину 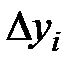 , называемую абсолютной разностью. Потребовав, чтобы сумма квадратов абсолютных разностей для всех точек была минимальной, найдем оптимальные параметры функции
, называемую абсолютной разностью. Потребовав, чтобы сумма квадратов абсолютных разностей для всех точек была минимальной, найдем оптимальные параметры функции 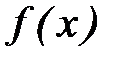 : если выполняется условие
: если выполняется условие
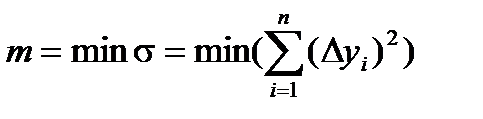 (10.2)
(10.2)
где 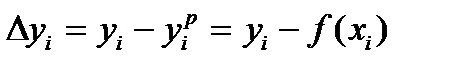 , то считается, что функция
, то считается, что функция 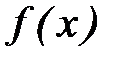 подобрана наилучшим образом.
подобрана наилучшим образом.
Рассмотрим все изложенное выше на примере линейной регрессии.
Линейная регрессия
Будем искать приближающую функцию в виде:

Абсолютная разность 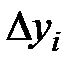 для
для  определяется следующим образом:
определяется следующим образом:

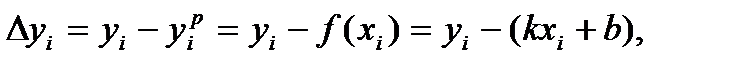 формулу (10.2) перепишем в виде:
формулу (10.2) перепишем в виде:
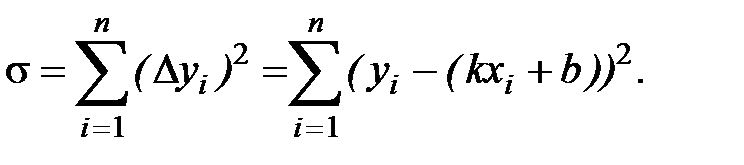
Рассматриваемая сумма является функцией с двумя параметрами 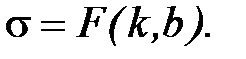 Задача сводится к отысканию минимума этой функции. Используем необходимое условие экстремума:
Задача сводится к отысканию минимума этой функции. Используем необходимое условие экстремума:
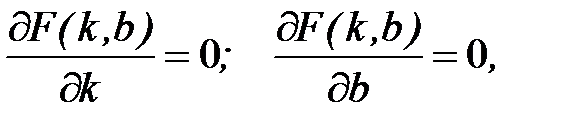
т.е. 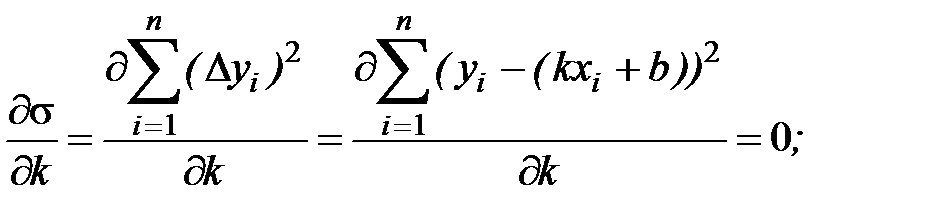
(10.3)
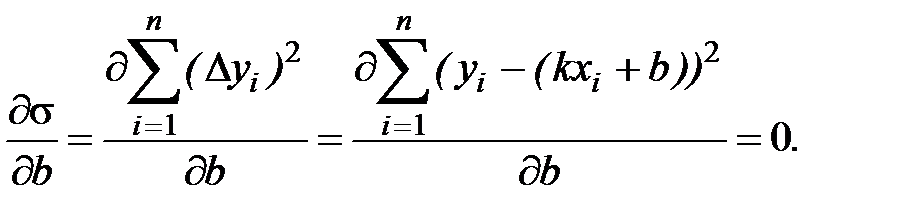
Решив систему двух уравнений с двумя неизвестными относительно параметров  и
и  , получим конкретный вид искомой функции
, получим конкретный вид искомой функции  Опуская математические выкладки, запишем выражения для искомых параметров:
Опуская математические выкладки, запишем выражения для искомых параметров:
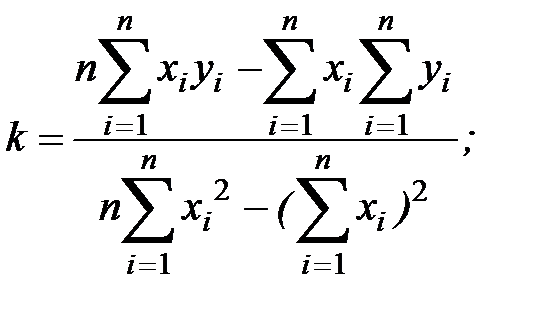
(10.4)
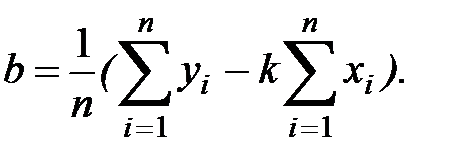
Рассчитав значение  , получим величину среднеквадратичной ошибки рассматриваемого приближения.
, получим величину среднеквадратичной ошибки рассматриваемого приближения.
Замечание: найденные значения  и
и  определяют точку экстремума
определяют точку экстремума 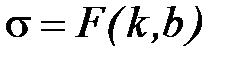 . Используя неравенство Коши-Буняковского можно доказать, что в этой точке функция принимает минимальное значение.
. Используя неравенство Коши-Буняковского можно доказать, что в этой точке функция принимает минимальное значение.
Как видно из рассмотренного примера, изменение количества параметров не приведет к искажению сущности самого подхода, изменится лишь количество уравнений в системе (10.3) (для 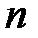 параметров соответственно будет записано
параметров соответственно будет записано 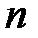 уравнений).
уравнений).
Чтобы подобрать формулу, выражающую зависимость между двумя величинами, если это зависимость найдена опытным путем, строят график этой зависимости. Полученный график сравнивают по внешнему виду с графиками, построенными при помощи известных формул. Формулы содержат небольшое число параметров (коэффициенты, показатели степеней и т.д.), изменением которых можно в той или иной степени менять вид кривой. Чтобы формула не оказалась слишком сложной, число параметров не должно быть велико. Обычно берут два-три параметра. При сравнении обращают внимание на наличие максимумов и минимумов, поведение функции при больших и малых значениях аргумента, выпуклость кривой вверх или вниз на отдельных участках и т.д. Выбрав среди известных графиков – подходящий график, следует подобрать такие значения параметров в формуле, чтобы разница между опытными значениями величины и значениями, найденными по формуле, не превышала ошибок эксперимента. Если эта разница получается слишком большой, берут другой подходящий график и повторяют попытку.
Ниже приведены наиболее употребимые формулы и соответствующие им графики.
Степенная зависимость имеет вид

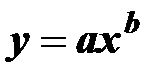 (10.5)
(10.5)
Во всех случаях 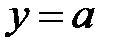 при
при 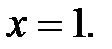 При
При  в точке
в точке 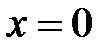 кривая касается оси абсцисс. В этом случае, чем больше
кривая касается оси абсцисс. В этом случае, чем больше  , тем ближе подходит кривая к оси абсцисс при
, тем ближе подходит кривая к оси абсцисс при  и тем быстрее она возрастает при
и тем быстрее она возрастает при 
При 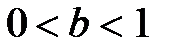 в точке
в точке  кривая касается оси ординат. При
кривая касается оси ординат. При  кривая ближе подходит к оси ординат, чем к оси абсцисс, при
кривая ближе подходит к оси ординат, чем к оси абсцисс, при  наоборот.
наоборот.
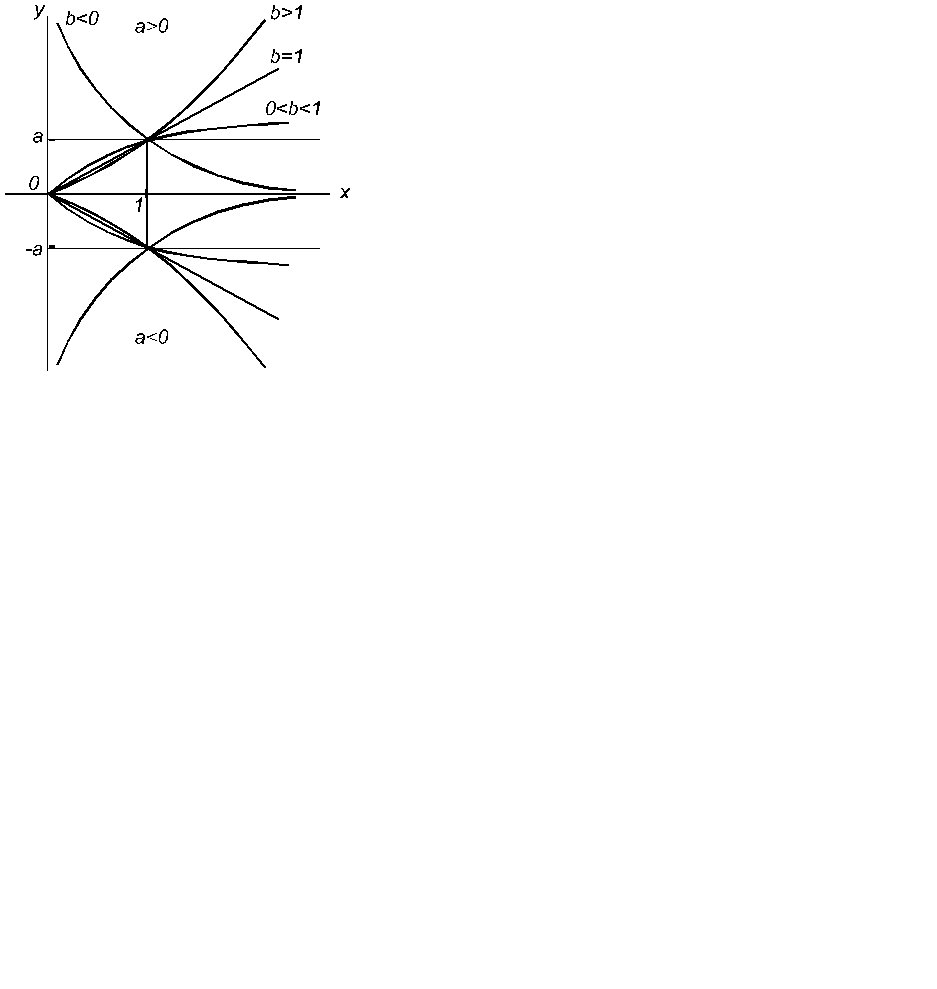
Рисунок 10.2 -График степенной зависимости
Покажем, как нахождение приближающей функции в виде геометрической регрессии может быть сведено к нахождению параметров линейной функции. Предполагая, что в исходной таблице 10.1 значения аргумента и функции положительны, прологарифмируем равенство (10.5) при условии 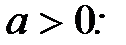
 (10.6)
(10.6)
Введем новую переменную 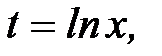 тогда
тогда  будет функцией от
будет функцией от 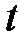 . Обозначим
. Обозначим 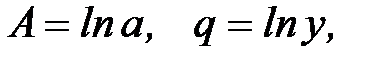 тогда равенство (10.6) примет вид:
тогда равенство (10.6) примет вид:

т.е. задача свелась к отысканию приближающей функции в виде линейной.
Практически для нахождения приближающей функции в виде степенной (при сделанных выше предположениях) необходимо проделать следующие операции:
1) по данной таблице 10.1 составить новую таблицу 10.2, прологарифмировав значения 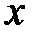 и
и 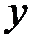 в исходной таблице;
в исходной таблице;
| Таблица 10.1 | Таблица 10.2 |

| 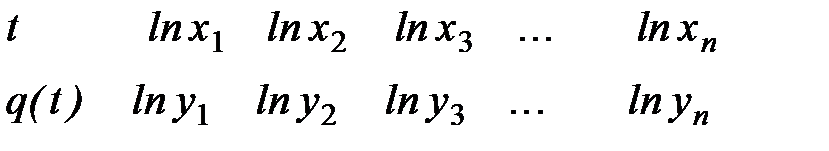
|
2) по новой таблице 10.2 найти параметры  и
и  приближающей функции вида
приближающей функции вида 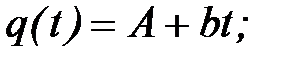
3) используя примененные обозначения, найти значения параметров 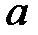 и
и  и подставить их в выражение (10.5).
и подставить их в выражение (10.5).
Окончательно получаем:
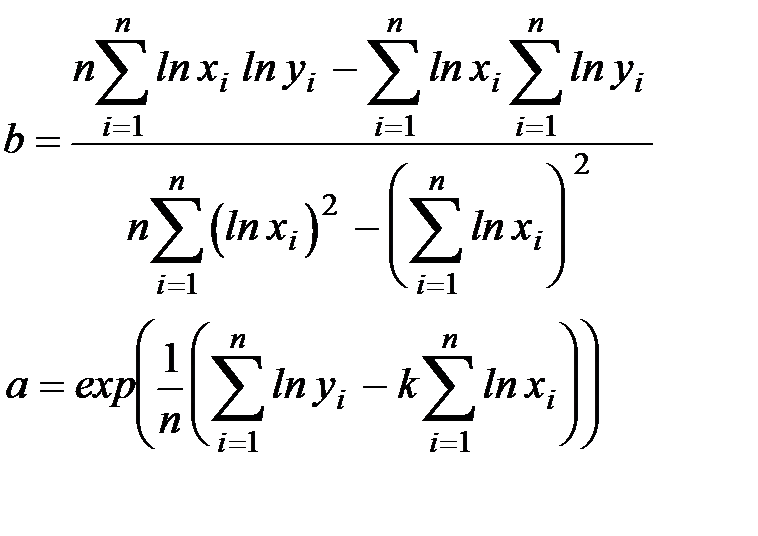 (10.7)
(10.7)
Задачи о приближении полиномов в смысле метода наименьших квадратов можно упрощенно решать в математической среде MATLAB:
Напомним, что задача приближения данных
 (10.8)
(10.8)
полиномом некоторой степени 
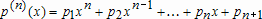 (10.9)
(10.9)
состоит в решении задачи минимизации
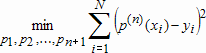 (10.10)
(10.10)
Запишем полином в виде
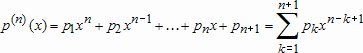 (10.11)
(10.11)
Тогда задача о построении полиномиального приближения сводится к поиску минимума следующей функции
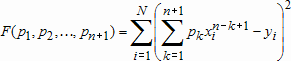 (10.12)
(10.12)
по переменным 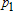 ,
, 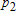 , ... ,
, ... , 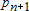 . Функция
. Функция 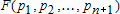 является квадратичной функцией (с неотрицательными коэффициентами при квадратах неизвестных), поэтому ее минимум достигается в той точке, где выполняются следующие условия:
является квадратичной функцией (с неотрицательными коэффициентами при квадратах неизвестных), поэтому ее минимум достигается в той точке, где выполняются следующие условия:
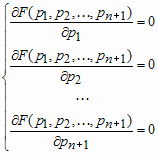
Взяв частные производные от 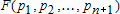 по
по 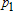 ,
, 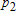 , ... ,
, ... , 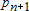 и приравняв их к нулю, получаем систему линейных алгебраических уравнений из (
и приравняв их к нулю, получаем систему линейных алгебраических уравнений из (  )-го уравнения для нахождения искомых коэффициентов
)-го уравнения для нахождения искомых коэффициентов 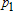 ,
, 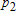 , ... ,
, ... , 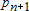 полинома
полинома  -ой степени, наилучшим образом в смысле наименьших квадратов приближающего данные
-ой степени, наилучшим образом в смысле наименьших квадратов приближающего данные

Эта система имеет вид:
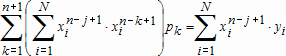

или в матричном виде
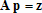
где

а элементы матрицы 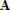 и вектора правой части системы
и вектора правой части системы  выражаются формулами
выражаются формулами
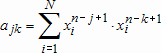
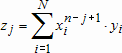
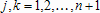
В принципе, ее можно решить и получить искомые коэффициенты полинома (это называется методом нормальных уравнений), однако в функции polyfit реализован несколько другой подход, более устойчивый к вычислительным ошибкам. Формируется прямоугольная матрица  из
из 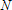 строк и (
строк и (  )-го столбца, элементами которой являются степени
)-го столбца, элементами которой являются степени  :
:
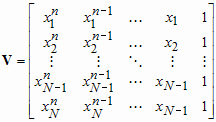
(Если 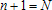 , то матрица
, то матрица  с точностью до перестановки столбцов в обратном порядке является известной матрицей Вандермонда). Несложно заметить, что матрица
с точностью до перестановки столбцов в обратном порядке является известной матрицей Вандермонда). Несложно заметить, что матрица 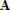 нашей системы линейных алгебраических уравнений и матрица
нашей системы линейных алгебраических уравнений и матрица  связаны между собой следующим образом:
связаны между собой следующим образом:
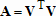
Аналогично, вектор  правой части системы уравнений
правой части системы уравнений 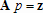 так же выражается через вектор
так же выражается через вектор
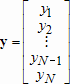
следующим образом:
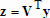
В функции polyfit при помощи функции qr пакета MATLAB разыскивается QR-разложение матрицы  , т.е. находятся такая ортогональная матрица
, т.е. находятся такая ортогональная матрица 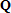 (квадратная матрица
(квадратная матрица 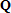 называется ортогональной, если произведение
называется ортогональной, если произведение 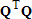 является единичной матрицей) и верхняя треугольная матрица
является единичной матрицей) и верхняя треугольная матрица  , что
, что 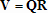 (более точно, ищется только первые
(более точно, ищется только первые  столбцов матрицы
столбцов матрицы 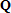 и не вся матрица
и не вся матрица  , а только первые
, а только первые  ее строк и столбцов). Далее система линейных уравнений
ее строк и столбцов). Далее система линейных уравнений

решается так:
1. вычисляется 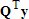 ;
;
2. решается система с верхней треугольной матрицей  и находится вектор
и находится вектор 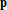 , содержащий коэффициенты
, содержащий коэффициенты 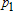 ,
, 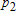 , ... ,
, ... , 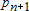 искомого полинома, который приближает данные в смысле наименьших квадратов.
искомого полинома, который приближает данные в смысле наименьших квадратов.
Ошибка приближения, т.е. значение
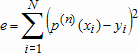
для найденного полинома
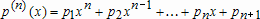
вычисляется по формуле

где евклидова норма вектора находится при помощи функции norm.
Функция polyfit может возвращать норму ошибки и матрицу  . Для этого ее следует вызвать с двумя выходными аргументами. В первом выходном аргументе (векторе) возвращаются найденные коэффициенты полинома, а второй выходной аргумент является структурой со следующими полями:
. Для этого ее следует вызвать с двумя выходными аргументами. В первом выходном аргументе (векторе) возвращаются найденные коэффициенты полинома, а второй выходной аргумент является структурой со следующими полями:
· R - содержит множитель  QR-разложения матрицы
QR-разложения матрицы  ;
;
· df - содержит значение 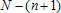
· normr - содержит норму ошибки полиномиального приближения  .
.
Например, для записи евклидовой нормы ошибки приближения в переменную e можно использовать следующие команды:
[p, S] = polyfit(x,y,4);e = S.normrВ ряде случаев функция polyfit может выдавать предупреждения, об этом подробно написано в следующем разделе.
Когда функция polyfit выдает предупреждения, плохая обусловленность, центрирование и масштабирование данных
Функция polyfit выдает предупреждения в нескольких случаях.
1. Если степень полинома 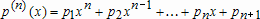 , приближающего данные
, приближающего данные  в смысле наименьших квадратов больше или равна числу данных, то выводится сообщение о том, что полином не единственный.
в смысле наименьших квадратов больше или равна числу данных, то выводится сообщение о том, что полином не единственный.
2. Если данные  такие, что при нахождении коэффициентов полинома при решении системы линейных алгебраических уравнений возможна большая вычислительная ошибка, то выводится предупреждение. О том, что возможна ошибка, свидетельствует число обусловленности матрицы
такие, что при нахождении коэффициентов полинома при решении системы линейных алгебраических уравнений возможна большая вычислительная ошибка, то выводится предупреждение. О том, что возможна ошибка, свидетельствует число обусловленности матрицы  ), которое оценивается в функции polyfit при помощи функции condest (она делает оценку числа обусловленности по отношению к первой матричной норме). Большое число обусловленности (в функции polyfit порог равен 1010) может привести к большим ошибкам при решении системы и нахождении коэффициентов полинома.
), которое оценивается в функции polyfit при помощи функции condest (она делает оценку числа обусловленности по отношению к первой матричной норме). Большое число обусловленности (в функции polyfit порог равен 1010) может привести к большим ошибкам при решении системы и нахождении коэффициентов полинома.
Большое число обусловленности может быть в нескольких случаях. Во-первых матрица
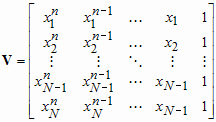
при 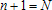 , как уже было замечено, является матрицей Вандермнода (с точностью до перестановки столбцов). Если точки
, как уже было замечено, является матрицей Вандермнода (с точностью до перестановки столбцов). Если точки  , в которых заданы значения данных
, в которых заданы значения данных 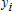 , равномерно распределены на отрезке [0, 1], то число обусловленности матрицы
, равномерно распределены на отрезке [0, 1], то число обусловленности матрицы 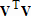 с ростом N ведет себя как число обусловленности матрицы Гильберта, которая является классическим примером плохо обусловленной матрицы с экспоненциально растущим числом обусловленности. Тогда число обусловленности матрицы
с ростом N ведет себя как число обусловленности матрицы Гильберта, которая является классическим примером плохо обусловленной матрицы с экспоненциально растущим числом обусловленности. Тогда число обусловленности матрицы  , совпадающее по значению с числом обусловленности множителя
, совпадающее по значению с числом обусловленности множителя  , входящего в QR-разложение
, входящего в QR-разложение  , будет вести себя как квадратный корень из числа обусловленности матрицы
, будет вести себя как квадратный корень из числа обусловленности матрицы 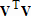 . Для N равномерно распределенных на отрезке [0, 1] точек
. Для N равномерно распределенных на отрезке [0, 1] точек  зависимость числа обусловленности матрицы
зависимость числа обусловленности матрицы  от N (при
от N (при 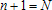 ) в полулогарифмической шкале представлена на следующем графике
) в полулогарифмической шкале представлена на следующем графике
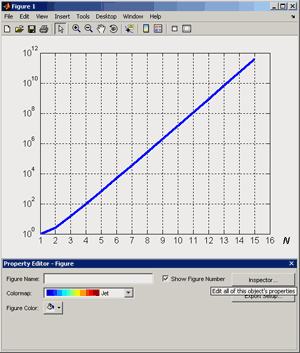
Рисунок10.1-зависимость числа обусловленности матрицы  от N (при
от N (при 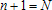 )
)
из которого видно, что даже для небольших значений число обусловленности будет превосходить 1010 и функция polyfit выдаст предупреждение о большой обусловленности, например:
>> N = 13; >> x = linspace(0,1,N); >> y = sin(x); >> p = polyfit(x, y, N-1) Warning: Polynomial is badly conditioned. Remove repeated data points or try centering and scaling as described in HELP POLYFIT.Для получения предыдущего графика число обусловленности прямоугольной матрицы  вычислялось как отношение ее наибольшего сингулярного числа к наименьшему, т.е.
вычислялось как отношение ее наибольшего сингулярного числа к наименьшему, т.е. 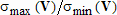 , где
, где 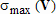 и
и  - максимальные и минимальные числа на диагонали матрицы
- максимальные и минимальные числа на диагонали матрицы 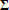 , входящей в сингулярное разложение матрицы
, входящей в сингулярное разложение матрицы 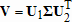 , где
, где  и
и  - ортогональные матрицы. Сами сингулярные числа определялись при помощи функции svd. Поскольку в функции polyfit используется сверху оценка для числа обусловленности, возвращаемая функцией condest, то предупреждение о превышении порога 1010 оценкой для числа обусловленности может наступить раньше. Для сравнения числа обусловленности матрицы
- ортогональные матрицы. Сами сингулярные числа определялись при помощи функции svd. Поскольку в функции polyfit используется сверху оценка для числа обусловленности, возвращаемая функцией condest, то предупреждение о превышении порога 1010 оценкой для числа обусловленности может наступить раньше. Для сравнения числа обусловленности матрицы  , полученного при помощи svd, и его оценки сверху, возвращаемой функцией condest, приведен следующий график
, полученного при помощи svd, и его оценки сверху, возвращаемой функцией condest, приведен следующий график

Рисунок10.2-Промежуточный график обработки данных
Если степень полинома  не в точности равна
не в точности равна 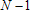 , но близка к числу точек N, в которых заданы данные, то число обусловленности тоже будет велико, как видно из следующего графика
, но близка к числу точек N, в которых заданы данные, то число обусловленности тоже будет велико, как видно из следующего графика
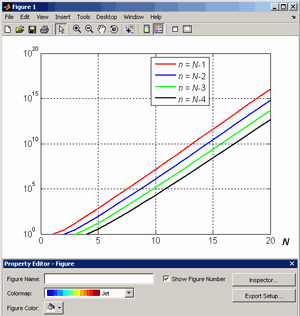
Рисунок10.3-Совмещенный график обработки данных
К примеру, приближение данных, заданных в двадцати равноотстоящих точках на отрезке [0, 1] полиномом тринадцатой степени уже приведет к предупреждению о плохой обусловленности:
>> N = 20; >> x = linspace(0, 1, N); >> y = sin(x); >> p = polyfit(x, y, 13) Контрольные вопросы1. В чем суть приближения таблично заданной функции по методу
наименьших квадратов?
Чем отличается этот метод от метода интерполяции?
2. Каким образом сводится задача построения приближающих функций в виде различных элементарных функций к случаю линейной функции?
3. Почему используется принцип минимума суммы квадратов абсолютных величин, а не суммы самих абсолютных величин?
4. Почему метод наименьших квадратов наиболее эффективен, если функция f(x) линейна относительно искомых параметров?
Дата добавления: 2015-12-11; просмотров: 3068;
