Алгоритм симплекс-метода. Рассмотрим систему ограничений и линейную форму вида:
Рассмотрим систему ограничений и линейную форму вида:
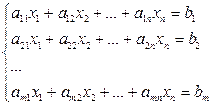 ; (2.64)
; (2.64)
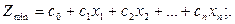 (2.65)
(2.65)
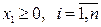 . (2.66)
. (2.66)
Используя метод Жордана-Гаусса, приведем записанную систему к виду, где выделены базисные переменные. Введем условные обозначения:
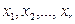 – базисные переменные;
– базисные переменные;
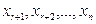 свободные переменные.
свободные переменные.
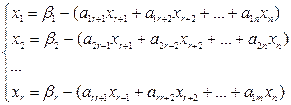 ; (2.67)
; (2.67)
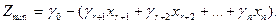 (2.68)
(2.68)
По последней системе ограничений и целевой функции Z построим табл. 2.5.
Таблица 2.5
Симплекс-таблица
| Базисные неизвестные | Свободные неизвестные | ||||
| Свободный член | xr+1 | xr+1 | … | xr+1 | |
| x1 | β1 | a1r+1 | a1r+2 | … | a1n |
| x2 | β2 | a2r+1 | a2r+2 | … | a2n |
| … | … | … | … | … | … |
| xr | βr | arr+1 | arr+2 | … | arn |
| Zmin | γ0 | γr=1 | γr+2 | … | γn |
Данная таблица называется симплекс-таблицей. Все дальнейшие преобразования связаны с изменением содержания этой таблицы.




 Алгоритм симплекс-метода сводится к следующему.
Алгоритм симплекс-метода сводится к следующему.
1. В последней строке симплекс-таблицы находят наименьший положительный элемент, не считая свободного члена. Столбец, соответствующий этому элементу, считается разрешающим.
2. Вычисляют отношение свободных членов к положительным элементам разрешающего столбца (симплекс-отношение). Находят наименьшее из этих симплекс-отношений, оно соответствует разрешающей строке.
3. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент.
4. Если имеется несколько одинаковых по величине симплекс-отношений, то выбирают любое из них. То же самое относится к положительным элементам последней строки симлекс-таблицы.
5. После нахождения разрешающего элемента переходят к следующей таблице. Неизвестные переменные, соответствующие разрешающей строке и столбцу, меняют местами. При этом базисная переменная становится свободной переменной и наоборот. Симплекс-таблица преобразована следующим образом (табл. 2.6).
6. Элемент табл. 2.6, соответствующий разрешающему элементу табл. 2.5, равен обратной величине разрешающего элемента.
7. Элементы строки табл. 2.6, соответствующие элементам разрешающей строки табл. 2.5, получаются путем деления соответствующих элементов табл. 2.5 на разрешающий элемент.
Таблица 2.6
Дата добавления: 2015-12-16; просмотров: 1241;
