Преобразование симплекс-таблицы
| Базисные неизвестные | Свободные неизвестные | ||||||||||
| Свободный член | xr+1 | x1 | … | xn | |||||||
| xr+2 | β1/a1r+2 | a1r+1/a1r+2 | 1/a1r+2 | … | a1n/a1r+2 | ||||||
| x2 | -a2r+2/a1r+2 | … | |||||||||
| … | … | … | … | … | … | ||||||
| xr | βr | arr+1 | -arr+2/a1r+2 | … | arn | ||||||
| Zmin | -γr+2/a1r+2 | … | |||||||||
8. Элементы столбца табл. 2.6, соответствующие элементам разрешающего столбца табл. 2.5, получаются путем деления соответствующих элементов табл. 2.5 на разрешающий элемент и берутся с противоположным знаком.
9. Остальные элементы вычисляются по правилу прямоугольника: мысленно вычерчиваем прямоугольник в табл. 2.5, одна вершина которого совпадает с разрешающим элементом, а другая – с элементом, образ которого мы ищем; остальные две вершины определяются однозначно. Тогда искомый элемент из табл. 2.6 будет равен соответствующему элементу табл. 2.5 минус дробь, в знаменателе которой стоит разрешающий элемент, а в числителе – произведение элементов из двух неиспользованных вершин прямоугольника.
10. Как только получится таблица, в которой в последней строке все элементы отрицательны, считается, что минимум найден. Минимальное значение функции равно свободному члену в строке целевой функции, а оптимальное решение определяется свободными членами при базисных переменных. Все свободные переменные в этом случае равны нулю.
11. Если в разрешающем столбце все элементы отрицательны, то задача не имеет решений (минимум не достигается).
Пример 18. Решение задачи симплекс-методом:
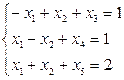
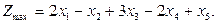
Приведем задачу к виду, допускающему применение симплекс-алгоритма:
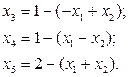
Подставим в выражение Zmax величины х3, х4, х5:
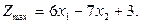
по алгоритму целевая функция должна стремиться к минимуму:
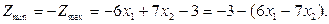
Составим симплекс-таблицу:
| Базисные неизвестные | Свободные неизвестные | ||||
| Свободный член | x1 | x2 | |||
| x3 | -1 | ||||
| x4 |
| -1 | |||
| x5 | |||||
| Zmin | -3 | -7 | |||
Разыскиваем в последней строке наименьший положительный элемент, в нашем примере он равен +6, первый столбец коэффициентов будет разрешающим. Определим отношение свободных членов к положительным элементам разрешающего столбца. Минимальное симплекс-отношение равно 1. Разрешающий элемент находится на пересечении строки переменной х4 и столбца х1.
Переходим к следующей таблице, используя правило прямоугольника:
| Базисные неизвестные | Свободные неизвестные | ||
| Свободный член | x1 | x2 | |
| x3 | |||
| x4 | -1 | ||
| x5 | -1 | ||
| Zmin | -9 | -6 | -1 |
В последней строке нет положительных элементов, следовательно, оптимальное решение найдено: 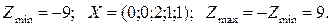
2.12. Примеры решения задач линейного программирования
на базе Excel
Электронные таблицы, или, как их еще называют, табличные процессоры – это удобное средство проведения расчетов и анализа результатов. Они предназначены для работы с большими таблицами чисел, в основном, для организации относительно несложных расчетов с большим количеством идентичных данных, например бухгалтерского учета. Значительное число задач в экономике составляют задачи распределения ресурсов и так называемые транспортные задачи. Наиболее часто математической моделью таких задач является задача линейного программирования. Ниже приводятся примеры решения таких задач с использованием среды MS Excel. Освоение основных приемов использования стандартных механизмов Excel при решении указанных задач, заключенных в надстройке «Поиск решения», позволит пользователям успешно решать большинство приведенных выше заданий с использованием этих технологий.
Дата добавления: 2015-12-16; просмотров: 1088;
