Геометрическим способом

Из рис. 2.8 следует, что по отношению к многоугольнику решений опорной эта прямая становится в точке С, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L₁и L₃. Для определения ее координат решим систему уравнений:

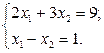
Оптимальный план задачи х₁= 2,4; x₂ = 1,4. Подставляя значения х₁ и х₂в линейную функцию, получим: 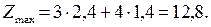Полученное решение означает, что объем производства продукции П₁ должен быть равен 2,4 ед., а продукции П₂– 1,4 ед. Доход, получаемый в этом случае, составит: Z = 12,8 д. е.

Геометрическим способом можно также решать задачи линейного программирования с числом переменных более двух. Для этого исходную задачу преобразуют методом Жордана-Гаусса.

Пример 17.

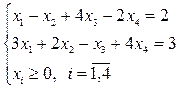
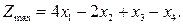
Используя метод Жордана-Гаусса, произведем два полных исключения x₁ и x₄:

.

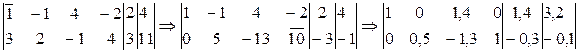В результате приходим к системе

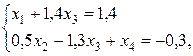
откуда

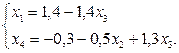
Подставляя эти значения в линейную функцию Z и отбрасывая в последней системе базисные переменные, получим задачу, выраженную только через свободные неизвестные х₁и x₃. Найдем максимальное значение линейной функции

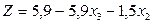
при следующих ограничениях:

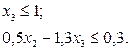
Построим многоугольник решений и линейную функцию в системе координат Х₂0Х₃(рис. 2.9).

Рис. 2.9. Геометрическая интерпретация решения задачи