Многосторонний коммерческий арбитраж

Валютный номинал	Тип трансакции	Возмож-ность рынка
I	r11	r12	r13	r14	r15	-1	-1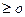
II	-1					r26			r29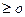
III		-1					r37	r38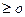
IV			-1					-1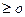
V				-1				r58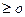
VI					-1		r67		-1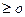
Размер транcакции	x1	x2	x3	x4	x5	x6	x7	x6	x9

При трансакции x₁ продажа единицы валютного номинала (ценных бумаг) IIпозволяет приобрести r₁₁единиц валютного номинала I. При трансакции x₇ взамен единицы валютного номинала I можно получить r₃₇ единиц валютного номинала IIIи r₆₇единиц валютного номинала VI. Остальные трансакции расшифровываются аналогично. Значения r_ijмогут быть дробными. Заметим, что при любой трансакции x_i (i = 1, 2, 3, 4, 5) каждый из валютных номиналов можно обменять на валютный номинал I. Следует обратить внимание на правило выбора знака перед показателями. Чтобы отличать куплю от продажи, будем соответственно использовать знаки "плюс" и "минус" перед показателями, характеризующими данную трансакцию.

Рассмотрим идеализированный случай, когда все трансакции коммерсанта N выполняются одновременно. Ограничения определяются единственным требованием – трансакция возможна лишь при условии, если коммерсант N располагает наличными ценными бумагами. Другими словами, количество проданных ценных бумаг не должно превышать количество приобретенных. Данные ограничения имеют вид

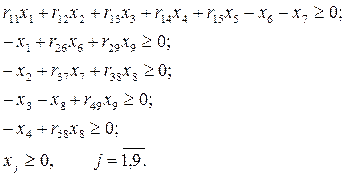
Пусть целевая функция представляет собой чистый доход, выраженный в единицах валютного номинала I, т.е. задача состоит в том, чтобы

.

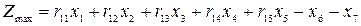Пример 15. Транспортная задача.

Имеются три поставщика и четыре потребителя однородной продукции. Известны затраты на перевозку груза от каждого поставщика каждому потребителю. Обозначим их 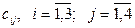. Запасы грузов у поставщиков равны 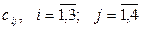. Известны потребности каждого потребителя 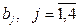. Будем считать, что суммарные потребности равны суммарным запасам:

.

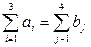Требуется составить такой план перевозок, чтобы обеспечить минимальные суммарные затраты при полном удовлетворении потребностей.

Введем переменные х_ij – количество груза, перевозимого от i-го поставщика j-му потребителю.

Ограничения задачи выглядят следующим образом:

• потребности всех потребителей должны быть удовлетворены полностью:

(2.58)

или в общем виде:

;

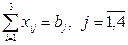• груз поставщика должен быть вывезен полностью:

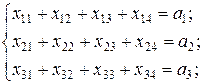(2.59)

или в общем виде:

;

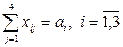• условие неотрицательности переменных:

.

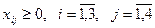Целевая функция – минимизировать суммарные затраты на перевозку:

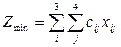. (2.104)

Количество поставщиков и потребителей в общем случае может быть произвольным ( ).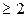

Мы рассмотрели девять примеров типовых задач линейного программирования. Обобщая их, можно сделать следующие выводы.

1. Ограничения в задачах линейного программирования могут быть выражены как равенствами, так и неравенствами.

2. Линейная функция может стремиться как к максимуму, так и к минимуму.

3. Переменные в задачах всегда неотрицательны.

Напомним, что от любой из вышеперечисленных задач можно перейти к канонической (основной) задаче линейного программирования.

2.11.3. Графические методы решения задач линейного
программирования

Графический способ решения задач линейного программирования целесообразно использовать для:

– решения задач с двумя переменными, когда ограничения выражены неравенствами;

– решения задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.

Запишем задачу линейного программирования с двумя переменными:

· целевая функция:

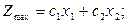(2.61)

· ограничения:

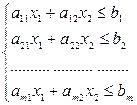; (2.62)

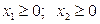. (2.63)

Каждое из неравенств (2.62) - (2.63) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми 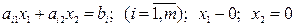. В том случае, если система неравенств (2.62) - (2.63) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых решений является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки равенств.

Областью допустимых решений системы неравенств (2.62)-(2.63) может быть:

– выпуклый многоугольник;

– выпуклая многоугольная неограниченная область;

– пустая область;

– луч;

– отрезок;

– единственная точка.

Целевая функция (2.61) определяет на плоскости семейство параллельных прямых, каждой из которых соответствует определенное значение Z.

Вектор 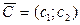с координатами с₁ и с₂, перпендикулярный к этим прямым, указывает направление наискорейшего возрастания Z, а противоположный вектор – направление убывания Z.

Если в одной и той же системе координат изобразить область допустимых решений системы неравенств (2.62-(2.63) и семейство параллельных прямых (2.61), то задача определения максимума функции Z сведется к нахождению в допустимой области точки, через которую проходит прямая из семейства Z = const и которая соответствует наибольшему значению параметра Z.

Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение.

Для определения данной вершины построим линию уровня 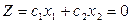, проходящую через начало координат и перпендикулярную вектору С = (с₁; с₂), и будем передвигать ее в направлении вектора 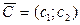до тех пор, пока она не коснется последней крайней (угловой) точки многоугольника решений. Координаты указанной точки и определяют оптимальный план данной задачи.

Заканчивая рассмотрение геометрической интерпретации задачи (2.61)-(2.63), отметим, что при нахождении ее решения могут встретиться случаи, изображенные на рис. 2.4-2.7. Рис. 2.4 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А. Из рис. 2.5 видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ.

На рис. 2.6 изображен случай, когда максимум недостижим, а на
рис. 2.7 – случай, когда система ограничений задачи несовместима.

Отметим, что нахождение минимального значения Z при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня Z передвигается не в направлении вектора 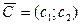, а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.

Для практического решения задачи линейного программирования (2.61)-(2.63) на основе ее геометрической интерпретации необходимо следующее.

1. Построить прямые, уравнения которых получаются в результате замены в ограничениях (2.62)-(2.63) знаков неравенств на знаки равенств.

2. Найти полуплоскости, определяемые каждым из ограничений задачи.

3. Определить многоугольник решений.

4. Построить вектор .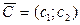

5. Построить прямую 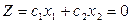, проходящую через начало координат и перпендикулярную вектору С.

6. Передвигать прямую 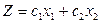в направлении вектора С, в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность функции сверху на множестве планов.

7. Определить координаты точки максимума функции и вычислить значение целевой функции в этой точке.

Пример 16.Рассмотрим решение задачи об ассортименте продукции (Пример 9) геометрическим способом.

Решение: Построим многоугольник решений (рис. 2.11). Для этого в системе координат Х₁0Х₂на плоскости изобразим граничные прямые:

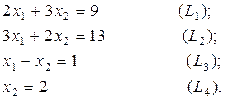
Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рис. 2.8 показаны стрелками. Областью решений является многоугольник OABCD.

Для построения прямой 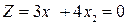строим вектор-градиент 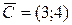и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z = 0 перемещаем параллельно самой себе в направлении вектора .

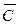Рис. 2.8. Решение задачи линейного программирования