Линейное программирование в решении оптимизационных задач

Оптимизационная задача – это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

В самом общем виде задача математически записывается так:

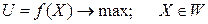,(2.28)

где ;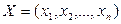

W – область допустимых значений переменных х₁, х₂, ..., х_n;

f(Х) – целевая функция.

Для того чтобы решить задачу оптимизации, достаточно найти ее оптимальное решение, т.е. указать 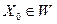такое, что 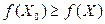при любом 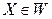, или для случая минимизации – 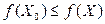при любом .

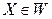Оптимизационная задача является неразрешимой, если она не имеет оптимального решения. В частности, задача максимизации будет неразрешимой, если целевая функция f(X)не ограничена сверху на допустимом множестве W.

Методы решения оптимизационных задач зависят как от вида целевой функции f(X), так и от строения допустимого множества W. Если целевая функция в задаче является функцией п переменных, то методы решения называют методами математического программирования.

В математическом программировании принято выделять следующие основные задачи в зависимости от вида целевой функции f(X) и от области W:

– задачи линейного программирования, если f(X)и W линейны;

– задачи целочисленного программирования, если ставится условие целочисленности переменных x_t, х₂, ..., х_п;

– задачи нелинейного программирования, если форма f(X)носит нелинейный характер.