Линейного программирования

Согласно рис. 2.9, линейная функция принимает максимальное значение в точке А, которая лежит на пересечении прямых L₂и Х₂=0. Ее координаты (0;0,23).Максимальное значение функции

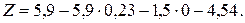
Для отыскания оптимального плана исходной задачи подставляем в преобразованную систему х₂и x₃. Окончательно получаем X= (1,078; 0; 0,23; 0,001).

Симплекс-метод

Для начала работы требуется, чтобы заданная система ограничений выражалась равенствами, причем в этой системе ограничений должны быть выделены базисные неизвестные. Решение задачи при помощи симплекс-метода распадается на ряд шагов. На каждом шаге от данного базиса Б переходят к другому, новому базису 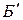с таким расчетом, чтобы значение функции Z уменьшалось, т.е. 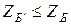. Для перехода к новому базису из старого удаляется одна из переменных и вместо нее вводится другая из числа свободных. После конечного числа шагов находится некоторый базис 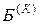, для которого 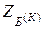есть искомый минимум для линейной функции Z, а соответствующее базисное решение является оптимальным либо выясняется, что задача не имеет решения.