Суть задачи о распределении ресурсов.
Предположим, имеются какие-либо ресурсы (сырье, рабочая, сила, оборудование):
R1, R2, … , Rm (2.69)
в количествах, соответственно:
b1, b2, … , bm (2.70)
единиц ресурсов.
С помощью ресурсов R1, R2, … , Rm могут производиться различные товары
T1, T2, … , Tm. (2.71)
Для производства одной единицы товара Tj необходимо aij единиц ресурса Ri (i = 1, 2, … , m; j = 1, 2, … , n), где m – количество ресурсов,n – количество видов продукции).
Каждая единица ресурса Riстоит di рублей (i = 1, 2, … , m). Каждая единица товара может быть реализована по цене сj(j = 1, 2, … , n).
Количество произведенных единиц должно быть ограничено спросом, так как рынок не может поглотить больше, чем kj единиц товара T (j = 1, 2, …, n).
Задача об оптимальном распределении ресурсов состоит в том, чтобы определить какое количество товара необходимо произвести для того, чтобы получить максимальную прибыль.
Введем некоторые обозначения:
x1, x2, … , xn – количества товаров T1, T2, … , Tn , запланированных к производству.
Условия спроса налагают на эти величины следующие ограничения:
x1 £ k1; x2 £ k2; … ; xn £ k2n ; (2.72)
Нельзя израсходовать ресурсов больше, чем имеется в наличии. Следовательно получаем ограничения по использованию ресурсов:
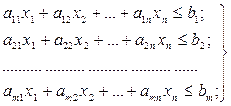 , (2.73)
, (2.73)
т.е. сумма произведений необходимых для производства количеств ресурсов на объем производства по каждому виду продукции не должна превышать имеющееся количество данного ресурса.
Теперь необходимо выразить прибыль L в зависимости от элементов решения x1, x2, … , xn, т.е. планируемых объемов производства продукции. Для этого сначала необходимо определить себестоимость товара.
Себестоимость sj единицы товара Tj будет равна:
sj = a1jd1 + a2jd2 + … + amjdm,, (2.74)
т.е. сумме произведений количеств требуемых ресурсов на их цены.
Вычислив себестоимость каждого вида продукции, получим ряд значений:
s1, s2, … , sn . (2.75)
Прибыль от реализации одного какого-либо вида продукции qi будет рассчитываться по формуле:
qi = ci – si; (2.76)
где ci – продажная (отпускная) цена какого-либо вида продукции,
si– себестоимость вида продукции; i = 1, 2, …, n; n – кол-во видов продукции.
В результате вычисления прибыли от реализации по каждому виду продукции получим набор значений:
q1, q2, … , qn. (2.77)
Общая прибыль от реализации всех видов продукции составит:
L = q1x1 + q2x2 + … + qnxn , (2.78)
где qi– прибыль от реализации единицы продукции; xi – объем производства данного вида продукции.
Задача сводится к тому, чтобы выбрать такие неотрицательные значения переменных x1, x2, … , xn (объемы производства продукции по каждому виду), чтобы удовлетворялись наложенные ограничения по ресурсам и соблюдались условия спроса на производимую продукцию, и при этом была бы получена максимальная прибыль, т.е. целевая функция принимала бы максимально возможное значение.
Для решения задачи распределения ресурсов используют симплекс-метод решения задач линейного программирования.
Пример решения.
В Excel имеется стандартный механизм разрешения подобных задач, заключенный в надстройке «Поиск решения». Для его использования необходимо активировать данную надстройку (рис. 2.10): Сервис ® Надстройки …
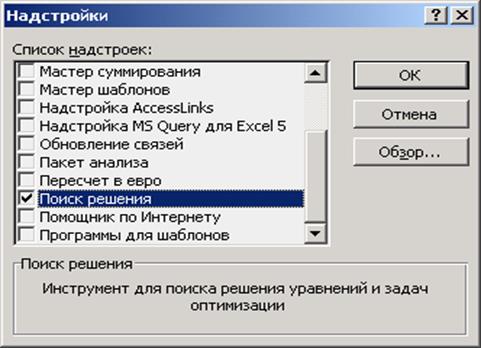
Рис. 2.10. Окно надстройки
Далее активировать элемент списка Поиск решения, как это показано на рисунке выше и нажать Ok. После этого опция
Поиск решения станет доступна в меню Сервис.
Теперь необходимо создать форму для решения задачи. Форма должна выглядеть, как показано на рисунке ниже. Серым цветом фона на рисунке отмечены ячейки, в которые пользователь должен ввести исходные данные. Черный цвет фона означает, что в данные ячейки должны быть введены формулы.
Какие же формулы должны быть введены в ячейки, отмеченные черным цветом? Это формулы, рассчитывающие соответствующие значения математических выражений, рассмотренных выше:
1. В ячейку E8 (рис. 2.11) должна быть введена формула, рассчитывающая целевую функцию (ЦФ).
Целевая функция, как было рассмотрено выше, для задачи распределения ресурсов представляет собой сумму произведений переменных «прибыль от реализации единицы продукции» (qi) на объем производства данной продукции (xi), т.е. L = q1x1 + q2x2 + … + qnxn.


Рис. 2.11. Форма заполнения основных формул
Так как qi - коэффициенты целевой функции, представленные в ячейках диапазона B8:D8, а xi – объемы производства, которые будут после решения задачи представлены в ячейках B5:D5, то формула расчета целевой функции должна рассчитывать сумму произведений ячеек B5:D5 на B8:D8.
Для расчета суммы произведений диапазонов ячеек предусмотрена математическая функция Excel «СУММПРОИЗВ».
= СУММПРОИЗВ(Список перемножаемых диапазонов).
Для расчета целевой функции необходимо в ячейку E8 ввести формулу
=СУММПРОИЗВ(B$5:D$5;B8:D8).
Теперь необходимо ввести ограничения использования ресурсов – систему неравенств-ограничений, исходные данные которой должны быть представлены в секции «Ограничения».
Каждое неравенство выражает ограничение объемов производства различных видов продукции имеющимся количеством данного ресурса и имеет левую и правую часть. Левая часть неравенства, как уже было рассмотрено, представляет собой сумму произведений количества ресурса, требуемого на производство единицы продукции, (aij), на объем производства данного вида продукции (xi). Правая часть неравенства отражает количество ресурса, которое имеется в распоряжении.
Так как объемы производства представлены в диапазоне ячеек B5:D5, а количество ресурса, необходимое для производства единицы продукции, представлено в диапазонах B12:D12 (для ресурса «Ресурс1»), B13:D13 (для ресурса «Ресурс2»), B14:D14 (для ресурса «Ресурс3»), то в ячейках E12:E14 соответственно должны быть формулы:
E12 = СУММПРОИЗВ(B$5:D$5; B12:D12);
E13 = СУММПРОИЗВ(B$5:D$5; B13:D13);
E14 = СУММПРОИЗВ(B$5:D$5; B14:D14).
т.е. суммы произведений соответствующих ячеек.
После ввода формул в ячейки форма примет следующий вид (рис. 2.12):
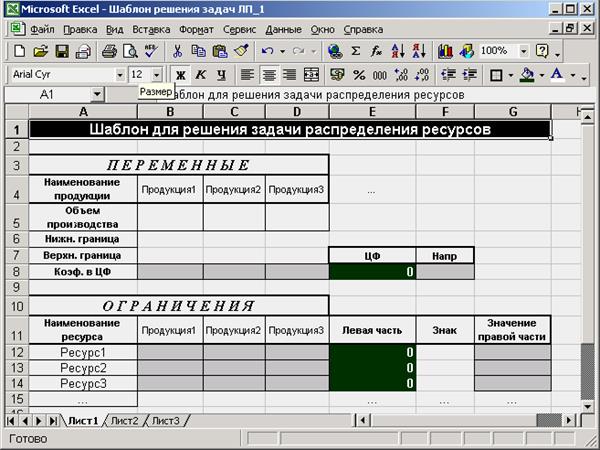
Рис. 2.12. Вид Фомы после ввода основных формул
Если включить режим отображения формул (Сервис ® Параметры … ® Вид ® Параметры окна ® Формулы ® Ok), то форма примет следующий вид (рис. 2.13):
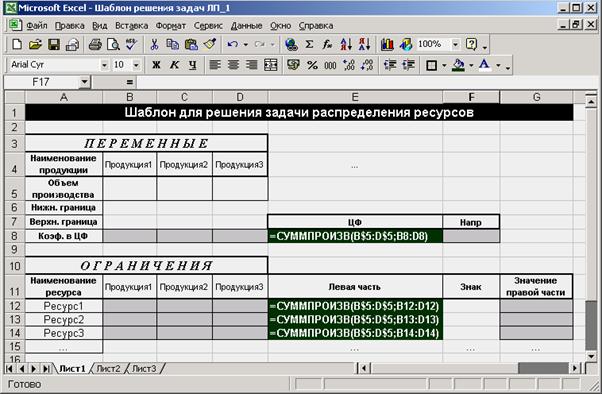
Рис. 2.13. Вид в режиме отображения формул
Отключить режим отображения формул можно аналогичным способом.
После ввода формул необходимо ввести исходные данные задачи.
Исходные данные.
Имеются три вида продукции, объемы производства обозначены соответственно x1, x2, x3. Для производства требуются три ресурса (например, труд, сырье, финансы). Использование каждого ресурса для единицы каждого вида продукции выражается коэффициентами при переменных x1, x2, x3 в следующей системе неравенств:
 ,
,
где первое неравенство – ограничение по ресурсу1, второе – по ресурсу2, третье – по ресурсу3. Правая часть неравенств отражает ограничение по использованию данного ресурса для производства.
Целевая функция выглядит следующим образом:
L = 80x1 + 100x2 + 50x3.
Из условия задачи видно, что значения коэффициентов при переменных первого уравнения необходимо ввести в ячейки B12, C12, D12 соответственно. Значения коэффициентов второго уравнения необходимо ввести в ячейки B13, C13, D13 формы, коэффициенты третьего уравнения – в ячейки B14, C14, D14.
Правую часть неравенств уравнений необходимо ввести соответственно для первого уравнения – в ячейку G12, для второго – в ячейку G13, третьего – G14.
В ячейки F12:F14 введем знаки неравенств <= (меньше или равно). Следует отметить, что введенные знаки никак не влияют на процесс расчета, однако они необходимы для понимания представленных в форме данных.
Введем коэффициенты при целевой функции в ячейки В8:D8. В ячейку F8 введем направление поиска оптимального значения целевой функции: минимум или максимум (значение данной ячейки также необходимо только для понимания представленных данных и не влияет на ход расчета).
В результате ввода данных форма примет следующий вид (рис. 2.14):
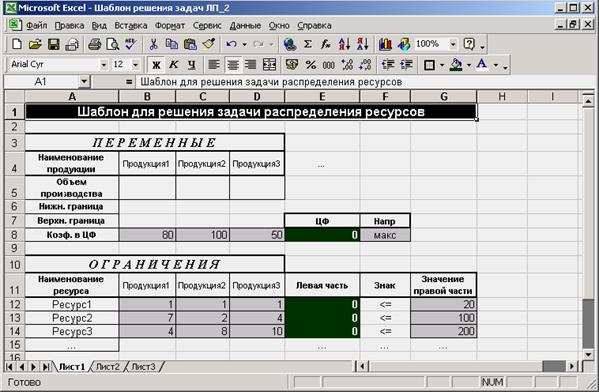
Рис. 2.14. Вид окна после ввода данных
Теперь необходимо задействовать механизм поиска оптимального решения (значений x1, x2, x3 для получения максимального значения целевой функции L): Сервис ® Поиск решения….
Появившийся в результате диалог «Поиск решения» (рис. 2.15) необходим для определения параметров расчета и его настроек:
1. В поле «Установить целевую ячейку» необходимо указать $E$8.
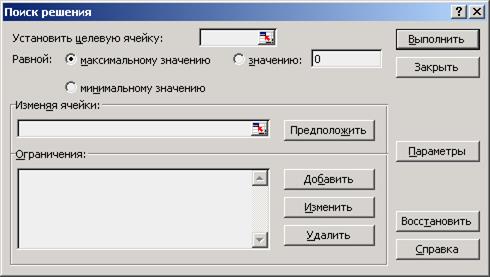
Рис. 2.15. Вид окна «Поиск решения»
2. Активировать переключатель «максимальному значению», что означает, что будет производиться максимизация значения целевой функции.
3. В поле «Изменяя ячейки» указать диапазон ячеек, в которые необходимо будет поместить значения объемов производства для каждого вида продукции, т.е. необходимо указать диапазон B5:D5.
4. В секции «Ограничения:» необходимо добавить настройки ограничений расчета, для чего необходимо:
– нажать кнопку «Добавить» (рис. 2.16)
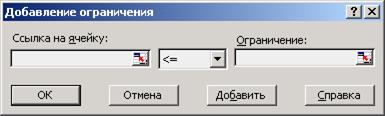
Рис. 2.16. Окно ввода ограничений
и в появившемся диалоге заполнить параметры ограничения для каждого неравенства:
– в поле «Ссылка на ячейку» выбрать ячейку, содержащую формулу левой части соответствующего неравенства, т.е. для первого неравенства выбрать ячейку E12;
– знак ограничения оставить без изменений;
– в поле «Ограничение» необходимо ввести имя ячейки, содержащей значение правой части неравенства (для первого неравенства это G12).
– рассмотренную процедуру повторить для каждого неравенства (рис. 2.17).
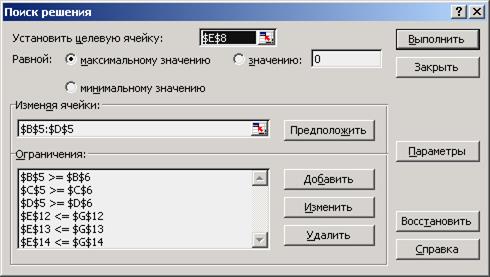
Рис. 2.17. Вид окна «Поиск решения» после ввода ограничений
Таким образом, после ввода параметров диалог «Поиск решения» примет следующий вид:
5. Нажать кнопку «Параметры» диалога «Поискрешения», что приведет к активации диалога «Параметры поиска решения» (рис. 2.18).

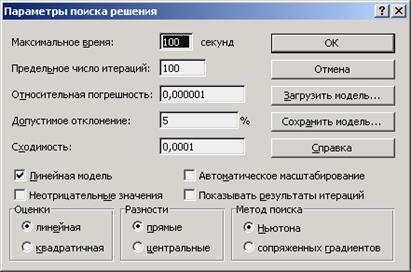
Рис. 2.18. Вид окна «Параметры поиска решения»
В появившемся окне диалога необходимо все оставить без изменения за исключением переключателя «Линейная модель» ® Нажать Ok.
6. В диалоге «Поискрешения» нажать кнопку «Выполнить» (рис. 2.19). Если оптимальное решение существует на экран будет выведен следующий диалог.
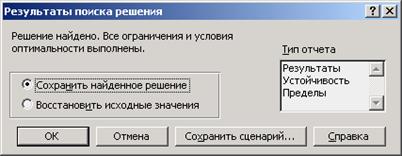
Рис. 2.19. Вид окна «Результаты поиска решения»
Диалог свидетельствует об успешном поиске оптимального решения.
Предложенное «Сохранить найденное значение» означает, что найденные значения объемов производства x1, x2, x3, максимизирующие целевую функцию прибыли будут помещены в соответствующие ячейки.
«Восстановить исходные значения» – означает отмену проведенного расчета.
Если решение найти не удалось, то пользователю будет выведен диалог о неуспешной попытке поиска оптимального решения.
Результат расчета представлен на рис. 2.20:
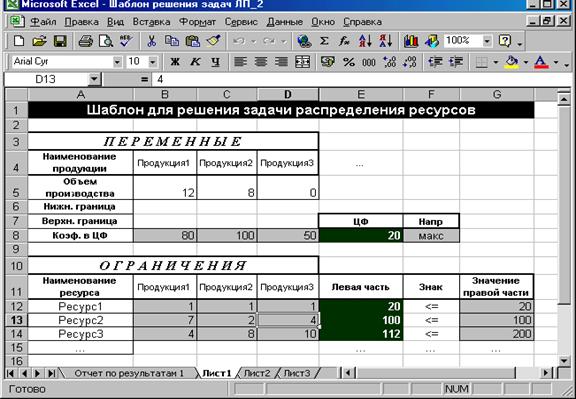
Рис. 2.20. Результат поиска решения
Из рисунка видно, что максимальная прибыль составит 20 денежных единиц, при этом необходимо запланировать выпуск продукции Продукция1 в объеме 12 единиц, продукции Продукция2– в объеме 8 единиц, а продукцию Продукция3 не производить вовсе в условиях установленных ограничений на использование ресурсов.
Варианты заданий для самостоятельного решения
Вариант 1
Для изготовления четырех видов продукции (П1, П2, П3, П4) используются три вида ресурсов (Р1, Р2, Р3). Другие условия представлены в следующей таблице:
| Ресурсы | Запас ресурсов, ед. | Нормы расхода сырья на единицу продукции, ед. | |||
| П1 | П2 | П3 | П4 | ||
| Р1 | |||||
| Р2 | |||||
| Р3 | |||||
| Прибыль от единицы продукции, ден. ед. |
Необходимо определить план выпуска продукции, при котором прибыль от ее реализации будет максимальной.
Вариант 2
Для изготовления четырех видов продукции (П1, П2, П3, П4, П5, П6, П7) используются пять видов ресурсов (Р1, Р2, Р3, P4, P5). Другие условия представлены в следующей таблице:
| Ресурсы | Запас ресурсов, ед. | Нормы расхода сырья на единицу продукции, ед. | ||||||
| П1 | П2 | П3 | П4 | П5 | П6 | П7 | ||
| Р1 | ||||||||
| Р2 | ||||||||
| Р3 | ||||||||
| Р4 | ||||||||
| Р5 | ||||||||
| Прибыль от единицы продукции, ден. ед. |
Необходимо определить план выпуска продукции, при котором прибыль от ее реализации будет максимальной.
Дата добавления: 2015-12-16; просмотров: 2450;
