Функции спектрального анализа и статистической обработки сигналов

Слова "спектральный анализ" в сознании многих пользователей MATLAB прочно ассоциируются с функцией fft (см. далее раздел "Функции преобразований дискретных сигналов"), выполняющей дискретное преобразование Фурье (ДПФ). Однако это всего лишь взаимно-однозначное линейное преобразование, дающее представление детерминированного сигнала в частотной области. Если же анализируемый сигнал является случайным, для него имеет смысл только оценка спектральной плотности мощности, для расчета которой приходится тем или иным способом выполнять усреднение имеющихся данных. Кроме того, в ряде случаев нам известна некоторая дополнительная информация об анализируемом сигнале, и эту информацию желательно учесть при спектральном анализе. Методы спектрального анализа случайных сигналов делятся на два больших класса — непараметрические и параметрические. В непараметрических (nonparametric) методах используется только информация, содержащаяся в отсчетах анализируемого сигнала. Параметрические (parametric) методы предполагают наличие некоторой статистической модели случайного сигнала, а процесс спектрального анализа в данном случае включает в себя определение параметров этой модели. Используется также термин "модельный спектральный анализ" (Model-Based Spectrum Analysis, MBSA).В пакете Signal Processing имеются функции, реализующие разнообразные методы спектрального анализа — как параметрические, так и непараметрические (необходимо еще раз подчеркнуть, что под спектральным анализом здесь имеется в виду оценка спектральной плотности мощности случайного процесса). Кроме того, имеются функции для получения других усредненных характеристик случайных дискретных сигналов.

• Спектр дискретного случайного процесса
• Непараметрические методы
• Параметрические методы
• Авторегрессионные методы
• Методы, основанные на анализе собственных чисел и векторов корреляционной матрицы
• Весовые функции (окна)
• Другие функции статистического анализа

Спектр дискретного случайного процесса. Для определения спектральных характеристик дискретного случайного процесса вычисляется средний спектр мощности его ограниченного по длине фрагмента, а затем длина фрагмента устремляется к бесконечности:

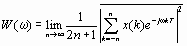. (12.1)

Здесь x(k) — отсчеты случайного процесса, T — период дискретизации. Черта сверху обозначает усреднение по ансамблю реализаций.

Кроме того, этот спектр можно выразить через корреляционную функцию случайного процесса:

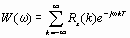. (12.2)

Это выражение представляет собой дискретный аналог теоремы Винера—Хинчина: спектр дискретного случайного процесса является преобразованием Фурье от его корреляционной функции.

Непараметрические методы.Как уже говорилось, при использовании непараметрических методов расчета спектра случайного процесса используется только информация, заключенная в отсчетах сигнала, без каких-либо дополнительных предположений. В пакете Signal Processing реализованы три таких метода — периодограмма, метод Уэлча (Welch) и метод Томсона (Thomson).

Периодограммой (periodogram) называется оценка спектральной плотности мощности, полученная по N отсчетам одной реализации случайного процесса согласно определению (естественно, не путем взятия предела, а усреднением конечного числа слагаемых). Если при расчете спектра используется весовая функция (окно), полученная оценка спектра мощности называется модифицированной периодограммой (modified periodogram):

Соотношение (12.2) выполняется только при бесконечном числе используемых отсчетов, поэтому при любом конечном N-периодограммная оценка спектральной плотности мощности оказывается смещенной — получается, что внутри суммы (12.2) корреляционная функция сигнала умножается на треугольную весовую функцию. Кроме того, можно показать, что периодограмма не является состоятельной оценкой спектральной плотности мощности, поскольку дисперсия такой оценки сравнима с квадратом ее математического ожидания при любом N. С ростом числа используемых отсчетов значения периодограммы начинают все быстрее флуктуировать — ее график становится все более изрезанным.

В пакете Signal Processing вычисление периодограммы (в том числе модифицированной) производится с помощью функции periodogram.

Для уменьшения изрезанности периодограммы необходимо применить какое-либо усреднение. Бартлетт (Bartlett) предложил разделять анализируемый сигнал на неперекрывающиеся сегменты, вычислять для каждого сегмента периодограмму и затем эти периодограммы усреднять. Если корреляционная функция сигнала на длительности сегмента затухает до пренебрежимо малых значений, то периодограммы отдельных сегментов можно считать независимыми. Уэлч (Welch) внес в метод Бартлетта два усовершенствования: использование весовой функции и разбиение сигнала на перекрывающиеся фрагменты. Применение весовой функции позволяет ослабить растекание спектра и уменьшить смещение получаемой оценки спектра плотности мощности ценой незначительного ухудшения разрешающей способности. Перекрытие сегментов введено для того, чтобы увеличить их число и уменьшить дисперсию оценки.

Вычисления при использовании метода Уэлча (он называется еще методом усреднения модифицированных периодограмм — averaged modified periodogram method) организуются следующим образом: вектор отсчетов сигнала делится на перекрывающиеся сегменты, каждый сегмент умножается на используемую весовую функцию, для взвешенных сегментов вычисляются модифицированные периодограммы, периодограммы всех сегментов усредняются. Метод Уэлча является наиболее популярным периодограммным методом спектрального анализа. В пакете Signal Processing он реализуется с помощью функции pwelch.

Метод Томсона, реализуемый функцией pmtm, основан на использовании вытянутых сфероидальных функций (prolate spheroidal functions). Эти функции конечной длительности обеспечивают максимальную концентрацию энергии в заданной полосе частот. Помимо собственно спектральной оценки, функция pmtm может возвращать ее доверительный интервал. Для вычисления вытянутых сфероидальных функций требуется некоторое время, поэтому при многократном использовании функции pmtm можно ускорить расчеты, заранее рассчитав необходимые для анализа функции и сохранив их в базе данных. Для работы с такой базой, (она представляет собой MAT-файл с именем dpss.mat) предназначено семейство функций, имена которых начинаются с букв dpss (dpss — расчет функций, dpssload — загрузка семейства функций из базы данных, dpsssave — сохранение семейства функций в базе данных, dpssdir — вывод каталога базы данных, dpssclear — удаление семейства функций из базы данных).