Проверка гипотезы о совпадении двух независимых средних значений
Рассмотрим следующую часто встречающуюся ситуацию. Из двух независимых экспериментов получены две группы результатов многократных измерений x1, x2,.......,xn1 и y1, y2,....yn2 нормально распределенных величин x и y. После обработки найдены оценки 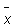 ,
, 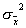 и
и 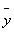 ,
, 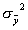 . Проверяют гипотезу о том, что
. Проверяют гипотезу о том, что 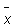 =
= 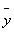 . Введем новую величину
. Введем новую величину 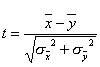 . (13.4)
. (13.4)
При справедливости равенства 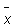 =
= 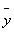 для n1
для n1 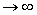 и n2
и n2 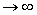 установлено, что при конечных значениях n1 и n2 распределение величины t близко к распределению Стьюдента, у которого
установлено, что при конечных значениях n1 и n2 распределение величины t близко к распределению Стьюдента, у которого
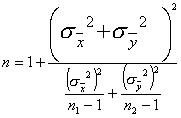 (13..5)
(13..5)
При уровне значимости a гипотеза о совпадении и подтверждена, если –t(a, n)<= t<= +t(a,n), чему соответствует доверительная вероятность a.
Общее среднее
Экспериментатору приходится сталкиваться с кругом проблем, которые возникают из-за различной точности выполнения измерений. Например, имеется набор результатов независимых измерений одной и той же постоянной физической величины, полученных в разных экспериментах. Естественно желание учесть всю имеющуюся информацию, чтобы найти более точное значение искомой величины. Как это сделать?
Допустим, что рассматривают n серий результатов независимых многократных измерений нормально распределенной величины x, в каждой из которых вычислены среднее 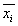 и дисперсия среднего s2i (i=1, 2,......, n), причем дисперсии полагают известными точно. По всем этим данным необходимо найти общую оценку среднего
и дисперсия среднего s2i (i=1, 2,......, n), причем дисперсии полагают известными точно. По всем этим данным необходимо найти общую оценку среднего 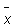 (общее среднее) и соответствующую дисперсию
(общее среднее) и соответствующую дисперсию 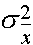 . Для нормального распределения величин
. Для нормального распределения величин 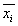 вокруг
вокруг 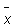 плотность вероятности:
плотность вероятности:
r( 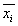 ) =
) = 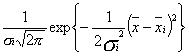 .
.
Плотность вероятности совместной реализации экспериментальных данных, или функция правдоподобия:
L( 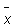 1,
1, 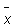 2, …….,
2, ……., 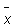 n) = r(
n) = r( 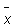 1)·r(
1)·r( 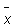 2)·….·r(
2)·….·r( 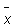 n) =
n) = 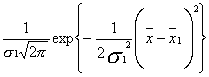 ·
· 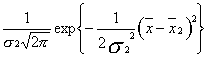 ....
....
Логарифм функции правдоподобия:
ln L = 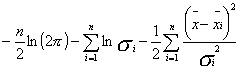 .
.
Максимум функции правдоподобия, совпадающий с максимумом ее логарифма, соответствует наибольшей вероятности получить в эксперименте имеющиеся данные многократных измерений. Аргументом функции правдоподобия является 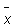 , поэтому ее максимум находят дифференцированием:
, поэтому ее максимум находят дифференцированием: 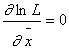 .
.
Полученное уравнение определяет наиболее вероятное значение искомой физической величины
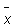 =
= 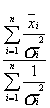 . (13.6)
. (13.6)
Этот результат задает общее среднее всех 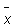 i , при вычислении которого учитывают точность каждого измерения, обратно пропорциональную дисперсии s2i. Происходит как бы «взвешивание» всех результатов для определения их роли в общем среднем, которое по этой причине называют еще средним взвешенным. Из (13.6) следует, что общее среднее может быть представлено как линейная комбинация независимых нормальных распределений величин
i , при вычислении которого учитывают точность каждого измерения, обратно пропорциональную дисперсии s2i. Происходит как бы «взвешивание» всех результатов для определения их роли в общем среднем, которое по этой причине называют еще средним взвешенным. Из (13.6) следует, что общее среднее может быть представлено как линейная комбинация независимых нормальных распределений величин 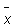 i с множителями
i с множителями
Ki = 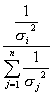 , в таком случае:
, в таком случае: 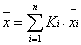 .
.
Значит, общее среднее также распределено нормально, а его дисперсию 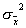 находят через дисперсию s2i:
находят через дисперсию s2i:
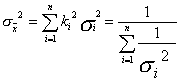 . (13.7)
. (13.7)
Полученные выражения легко проверить для случая, когда величины 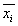 представляют собой результаты одного многократного измерения
представляют собой результаты одного многократного измерения 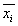 = xi , а их дисперсии s2i относятся к общему распределению величины x и равны между собой: s2i =
= xi , а их дисперсии s2i относятся к общему распределению величины x и равны между собой: s2i = 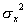 . Тогда
. Тогда 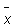 =
= 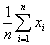 и
и 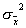 =
= 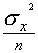 , как уже было получено для результата прямого многократного измерения Выше дисперсии s2i полагались заданными точно. Только тогда (13.7) дает точное значение
, как уже было получено для результата прямого многократного измерения Выше дисперсии s2i полагались заданными точно. Только тогда (13.7) дает точное значение 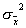 . Вместо дисперсий s2i в выражениях (13.6) и (13.7) можно использовать погрешности окончательных результатов Dxi , вычисленные при помощи коэффициентов Стьюдента для заданного значения доверительной вероятности (одинаковой для всех результатов). В этом случае (13.7) будет задавать верхнюю оценку погрешности общего среднего Dx для того же значения доверительной вероятности.
. Вместо дисперсий s2i в выражениях (13.6) и (13.7) можно использовать погрешности окончательных результатов Dxi , вычисленные при помощи коэффициентов Стьюдента для заданного значения доверительной вероятности (одинаковой для всех результатов). В этом случае (13.7) будет задавать верхнюю оценку погрешности общего среднего Dx для того же значения доверительной вероятности.
Контрольные вопросы
1.Что называют средним взвешенным?
2.Понятие доверительный интервал
3. Объясните смысл величины, названной как экспериментальное среднее
Дата добавления: 2015-12-11; просмотров: 1158;
