Проверка гипотезы о совпадении экспериментального среднего и известного значения величины

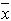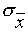Рассмотрим набор результатов x₁, x₂,.....,x_n многократного измерения нормально распределенной величины x . Из этих данных получены оценки и . Проверяется гипотеза о том, что 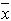=x₀, где x₀ – заданное значение измеряемой величины, точно известное, например, из расчетов или справочных таблиц.

Введем новую величину, содержащую как экспериментальное среднее, так и заданное значение:

t = 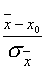. (13..1)

Если равенство 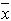= x₀ справедливо для n 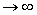, то распределение величины t при конечном количестве измерений n будет распределением Стьюдента.

Форма этого распределения показана на рис.13.1. Оно симметрично относительно нуля и при увеличении n переходит в нормальное распределение с параметрами 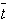= 0 и s_t²=1. При малых n максимум распределения Стьюдента ниже максимума нормального распределения, а на крыльях, т.е. при удалении от центра, график распределения Стьюдента проходит выше.

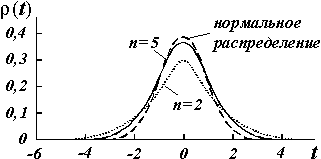
Рисунок 13.1- Распределение Стьюдента для разного количества измерений.

Каковы причины, приводящие к появлению распределения Стьюдента? Для ответа на этот вопрос мысленно представим эксперимент, в котором проводят многократные измерения величины x , нормально распределенной вокруг нуля ( 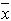=0) с точно известной дисперсией s². Последовательно выполним серии из n измерений, в каждой из которых результаты (x¹, x²,….,xⁿ)_j используем для получения 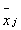и 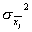, где символ j обозначает порядковый номер многократного измерения. Значения 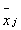и 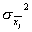являются экспериментальными оценками среднего и дисперсии, поэтому они, как и сама случайная величина x, подвержены воздействию случайного фактора, приводящего к различным наборам данных, реализуемым в каждой серии результатов многократного измерения. Среднее 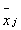находят согласно выражению 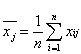, оно представляет собой сумму нормально распределенных величин. Значит, распределение величин 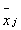также окажется нормальным с дисперсией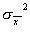 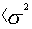Если распределения x и 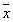построить на одном графике, то r( 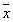, n) окажется выше и несколько уже распределения r(x) , что хорошо видно на рисунке 13.2.

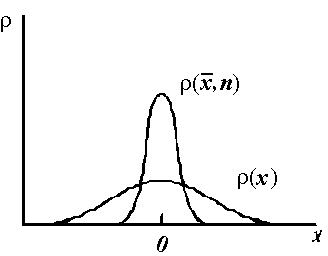
Рисунок13.2- Получение распределения Стьюдента.

Процедура получения r(x) сводится к построению соответствующих гистограмм. Распределение r(x) строят из полного набора результатов, а r( 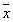, n)– только из набора 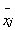, причем в обоих случаях j 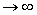. В пределе среднее значение распределения r( 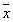,n) стремится к нулю, а его дисперсия – к 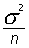. Перестроим полученные распределения в одном масштабе, для чего введем новые переменные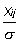: t'= и t= 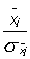. Распределение r(t') окажется нормальным распределением с нулевым средним и единичной дисперсией, аr(t, n) – распределением Стьюдента, которое формируется из-за наложения статистики оценки 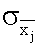на гауссову статистику величины 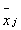. Именно эти распределения приведены на рисунке 13.1.

Если теперь сравнить величину t, введенную в (13.1), и величину t, использованную в проведенном рассмотрении, то можно заметить, что в (13.1) вместо 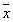используется 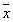–x₀ ( 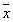=x₀ при n 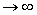). Однако статистика величины 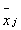не может зависеть от линейного сдвига координаты по оси x, а значит, величина t в (13.1) также распределена по Стьюденту. Плотность вероятности распределения Стьюдента описывает выражение:
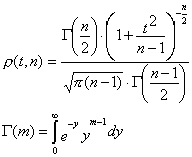(13.2)

где n – количество проведенных измерений, а m>0.

Зная r(t, n) , не составит труда вычислить интервал [ ^{-t(a, n), +t(a, n)}], в который величина t попадет с заданной вероятностью a. Для этого необходимо решить уравнение

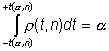. (13.3)

Вероятность a определяет так называемый уровень значимости .

Если значение t = 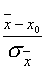попадает в указанный интервал, то это свидетельствует в пользу справедливости гипотезы о совпадении 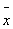и x₀ при уровне значимости a. Чем больше a, тем шире интервал, тем больше вероятность обнаружить в нем величину t , относящуюся к эксперименту при 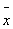=x₀ . Найдем интервал возможного изменения величины 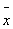. Воспользуемся

,

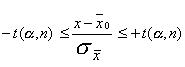откуда .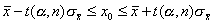

При попадании заданного значения x₀ в найденный интервал вокруг гипотезу о совпадении 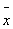и x₀ нужно расценивать как справедливую для уровня значимости a.

Сопоставив (13.3) с (13.4), можно заключить, что уровень значимости является ни чем иным, как доверительной вероятностью, а рассчитанный интервал возможного изменения x₀ – доверительным интервалом. Тогда t(a, n) – коэффициент Стьюдента. В этих терминах картина проведенного сравнения 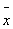и x₀ выглядит следующим образом. Если при сравнении 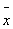и x₀ значение x₀ попадает в доверительный интервал вокруг, то статистическим выводом является заключение о совпадении сравниваемых величин с доверительной вероятностью a.

Как уже отмечалось, в измерениях принято использовать вероятность a=0,68 , в пределе при больших n задающую интервал ± 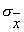вокруг 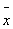. Для повышения достоверности сравнения, используют уровень значимости a=0,997, определяющий более широкий интервал, в пределе стремящийся к ±3 .

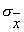Для малых n за погрешность прямого многократного измерения величины x естественно принимать Dx = t(a,n) 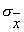, как и предлагалось при обсуждении погрешностей прямых измерений. Именно в интервале, задаваемом Dx, могут оказаться точные величины x₀, совпадающие с результатом измерения 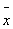. В случае косвенного измерения результаты прямых измерений определяют погрешность результата косвенного измерения. При этом необходимо выбрать равный уровень значимости для результатов всех прямых измерений, который переносится на уровень значимости результата косвенного измерения.