Определение параметров линейной зависимости из графика

После нанесения на график экспериментальных точек по ним «на глаз» проводят прямую линию. Строят ее таким образом, чтобы точки в среднем одинаково располагались по обе стороны от прямой. На рис.8.1 это прямая: 1-2. На ней выбирают две точки (1 и 2) максимально удаленные друг от друга.

Рисунок 9.1 - Графическая обработка линейной зависимости.

Их координаты x1, y1 и x2, y2 подставляют в (9.1) для получения двух уравнений с неизвестными a и b:

y1=ax1+b

y2=ax2+b ,

из которых находят:

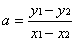, . (9.2)

Для оценивания a и b строят две дополнительные прямые симметричные линии относительно прямой 1-2, чтобы экспериментальные точки, в основном, располагались между ними. Если на графике имеются точки, которые отстоят от основной прямой 1-2 более, чем на утроенное среднее расстояние точек до прямой (это хорошо заметно уже при рассматривании графика – на рис.8.1 такой точкой является точка А), то их отбрасывают и не используют при построении дополнительных прямых. Соответствующие измерения, скорее всего, содержат промахи. Дополнительные прямые линии определяют «коридор погрешностей» эксперимента, внутри которого находится исследуемая линейная зависимость. Предельные случаи хода этой зависимости получатся, если провести прямые через противоположные углы «коридора» (прямые 4-5 и 6-7). Тем же способом, что и для основной прямой 1-2, находят параметры предельных прямых a₁, b₁ и a₂, b₂ . Оценки погрешностей:

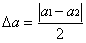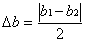, , . (9.3)

Может оказаться, что теоретическую зависимость между измеряемыми величинами предполагают линейной, а экспериментальные точки явно не ложатся на прямую. Проведение по ним прямой, как это сделано на рис.8.2, неправомерно. Расхождение между теоретической и экспериментальной зависимостями свидетельствует о наличии систематических погрешностей, которые должны быть выявлены и учтены при обработке результатов. Иначе экспериментатору остается только констатировать расхождение модели с экспериментом.

Рисунок 9.2- Пример необоснованной интерпретации экспериментальной зависимости как линейной.

Часто линейная зависимость является приближенно справедливой в ограниченном интервале изменения физических величин. В таком случае необходимо определить границы применимости линейной зависимости и указать их при анализе результатов эксперимента.

Метод парных точек

В некоторых физических экспериментах основной интерес представляет только угловой коэффициент (параметр а) зависимости (9.1). Для оценивания значения коэффициента и определения его погрешности удобен метод парных точек. Он заключается в следующем. После нанесения на график экспериментальных точек из них выбирают пары, в которых точки отстоят друг от друга примерно на одинаковое расстояние. Желательно, чтобы это расстояние было максимально возможным. Через каждую пару проводят прямую, а затем согласно (9.2) вычисляют угловые коэффициенты всех прямых. Из получившегося набора коэффициентов по правилам обработки данных прямых измерений определяют среднее значение коэффициента и его погрешность. Их принимают за результат измерения искомого параметра зависимости (9.1).

Следует отметить, что аналогичным образом в зависимости (9.1) можно найти свободный член (параметр b). По парам точек согласно (9.2) вычисляют свободные члены всех полученных прямых. Затем указанным выше способом рассчитывают среднее значение и погрешность.

Контрольные вопросы

1. Почему аналитики, теоретическую зависимость стремятся преобразовать к линейной зависимости?

2. В чем преимущества метода наименьших квадратов после проведения линеаризации?

3. Назовите правила, используемым для обработки результатов косвенных измерений.