Частотные характеристики стохастического сигнала

Автокорреляционная функция 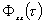описывает временные параметры стохастического сигнала. Преобразовывая ее по Фурье, можно получить адекватное частотное описание стохастического сигнала, Преобразованная по Фурье автокорреляционная функция называется спектральной плот­ностью сигнала и обозначается через :

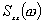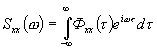. (6.6)

Так как 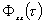представляет собой чётную функцию, то спектральная плотность всегда является чётной и действительной функцией 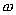. Поэтому эта зависимость идентична следующему:

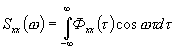. (6.7)

Обратное преобразование осуществляют по следующим формулам:

(6.8)

Спектральную плотность физически можно интерпретировать как плотность мощности сигнала, распределенную по частотам .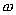

Из последнего соотношения следует:

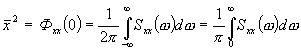(6.9)

Информация о тенденции к сохра­нению стохастического сигнала, содержащаяся в автокорреля­ционной функции, содержится также и в спектральной плот­ности. Слабая тенденция к поддержанию сигнала означает, что уже при малом смещении времени 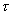величины 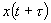и 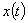становятся некоррелированными. Этому соответствует быстро спадающая с увеличением 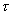автокорреляционная функция. В спек­тральной плотности это проявляется в том, что «мощность» сиг­нала распределена и на высоких частотах. Если сигнал имеет широкочастотный спектр, то он быстро изменяется во времени.

При численной обработке диаграмм измерительных приборов, при аналого-цифровых преобразованиях, при считывании измерительных сигналов посредством переключения точек измерения, при использовании точечных регистраторов приходится считаться с потерей информации.

Импульсный сигнал можно представить в виде произведения последовательности стробирующих импульсов на первоначальный измерительный сигнал. Особый интерес представляет описание таких сигналов в частотной области.

Последовательность стробирующих импульсов является пе­риодической функцией, поэтому ее можно представить в виде ряда Фурье, обозначаемого через :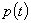

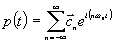, (6.10)

где 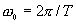— круговая частота следования стробирующих импульсов.

Тогда воспроизводящий импульсный сигнал 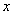(t) можно опи­сать следующим образом:

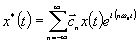. (6.11)

Изображение по Лапласу сигнала 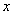(t) находим с помощью теоремы смещения:

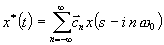. (6.12)

Контрольные вопросы

1.Смысл уравнения ряда Фурье при описании гармонического периодического сигнала

2.Смысл автокорреляционной функции

3.Что такое спектральная плотность сигнала?

4.Для чего нужно обратное преобразование Фурье?