Анализ технологической погрешности

Технологические погрешности

Анализ технологической погрешности

Расчетные значения ВП измерительных звеньев, полученные из условия наилучшего приближения расчетной ФП к номинальной, не могут быть реализованы в конструкции звена абсолютно точно. Причиной этого является технологический разброс размеров ВП, возникающий при изготовлении и сборки элементов измерительного звена. Отклонению действительной ФП от расчетной содействует также воздействие ВДФ, таких как моменты трения и дисбаланса, внутренние шумы активных элементов и т.д.

Технологическая погрешность определяется как разность между действительной и расчетной ФП:

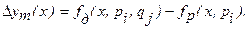
Здесь p_i - действительные значения ВП;

q_j действительные значения ВДФ, номинально равные нулю и поэтому формально не входящие в выражение для расчетной ФП.

Можно ввести и единое обозначение для ВП и ВДФ:

ВП: р_i; i=0, I, 2, ….m;

ВДФ: q_j=p_i; i=m+j =m+1, m+2, ……m+n.

Обозначим через

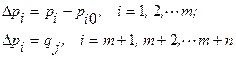
первичные погрешности элементов измерительного эвена, обусловленные технологическим процессом их изготовления.

Искусственно введем ВДФ в выражение для действительной ФП. Учитывая, что все 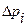, как правило, малые величины, выражение для технологической погрешности можно представить степенным рядом:

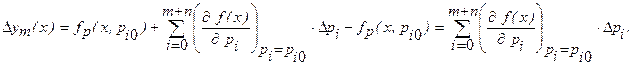
Индекс 0 у частной производной означает, что она вычисляется при расчетных значениях всех ВП. Погрешность, приведенная ко входу измерительного звена, при линейной номинальной ФП:

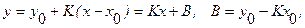
получается делением не статическую чувствительность К:

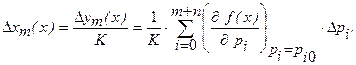
Величины, стоящие здесь перед первичными ошибками 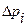, называются коэффициентами влияния соответствующих первичных ошибок на технологическую погрешность измерительного

звена:

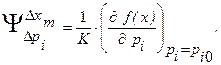
Произведения коэффициентов влияния па первичные ошибки дают нам частные технологические погрешности:

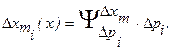
Тогда сумма частных погрешностей представляет собой суммарную технологическую погрешность звена

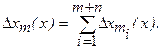
Полученные соотношения имеют ряд особенностей, которые заслуживают отдельного рассмотрения.

I) При разложении в степенной ряд мы учли только линейные члены. В некоторых случаях существенное значение имеют в 6олее высокие члены разложения. Поэтому иногда бывает удобно говорить не о коэффициентах влияния, а о функциях влияния первичных ошибок на технологическую погрешность. При этой функция влияния - это просто зависимость частной технологической погрешности от соответствующей первичной ошибки.

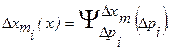
2) Иногда первые производные по ВП н, особенно часто, по ВДФ обращаются в куль при расчетных значениях ВП. Тогда коэффициенты влияния - это половины вторых производных, и они описывают влияние квадратов первичных ошибок:

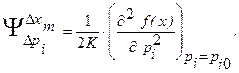
Выражение для соответствующей частной погрешности принимает вид:

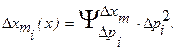
3) Коэффициенты влияния являются функциями входной величины или информативного параметра выходного сигнала, если расчетная функция преобразования нелинейная.

Разлагая выражение для ФП в степенной ряд по входной величине, имеем:

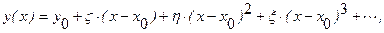
где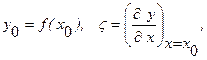

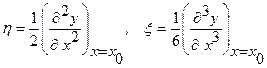параметры функции преобразования.

Поэтому коэффициент влияния - это сумма

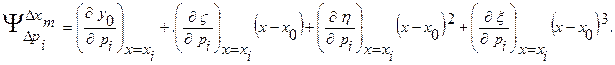
Это позволяет в технологической погрешности выделить отдельно:

аддитивную составляющую:

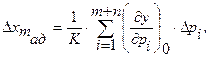
мультипликативную составляющую:

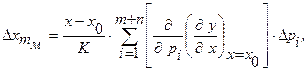
квадратурную составляющую:

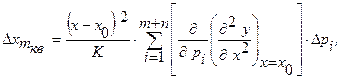
и так далее.

4) Некоторые ВДФ, номинально равные нулю, приводят к возникновению периодических частных погрешностей. Сюда относятся, например, погрешности зубчатого колеса, эксцентриситеты и т.д. В результате возникает периодическая составляющая технологической погрешности:

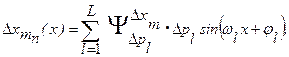
где 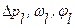- амплитудное значение, частота и фаза l -того ВДФ.

5). Местные погрешности формы контактирующих поверхностей элементов преобразователя, неравномерности намоток потенциометров и катушек индуктивности, непостоянство чувствительности по рабочей поверхности фотоприемников в прочие аналогичные факторы вызывают появление частных погрешностей, существенно не линейно или даже случайно (в массе экземпляров), изменяющихся в диапазоне преобразования. В результате возникает составляющая, сложным образом зависящая от входной величины

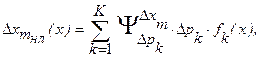
где 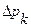- наибольшее значение данного возмущения; 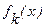- функция, характеризующая его изменение от входной величины.

6) В составе технологической погрешности необходимо учесть и погрешность обратного хода, возникающую за счет трения и зазоров в опорах подвижных систем и за счет гистерезисных явлений в электромагнитных и упругих элементах измерительного звена.