Вероятностные характеристики технологической погрешности
Вероятностными характеристиками технологической погрешности являются:
- математическое ожидание погрешности,
- дисперсия или стандартное отклонение погрешности.
Плотность распределения технологической погрешности 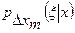 определять специально не нужно, поскольку погрешность средства измерений в целом в большинстве случаев, на основании центральной предельной теоремы теории вероятностей, можно считать распределенной нормально или почти нормально. Поэтому для определения вероятностных характеристик суммарной погрешности достаточно только математическое ожидание и дисперсию частных технологических погрешностей.
определять специально не нужно, поскольку погрешность средства измерений в целом в большинстве случаев, на основании центральной предельной теоремы теории вероятностей, можно считать распределенной нормально или почти нормально. Поэтому для определения вероятностных характеристик суммарной погрешности достаточно только математическое ожидание и дисперсию частных технологических погрешностей.
Отдельные первичные ошибки, а поэтому и частные погрешности в большинстве случаев являются независимыми случайными величинами. Поэтому математическое ожидание погрешности:
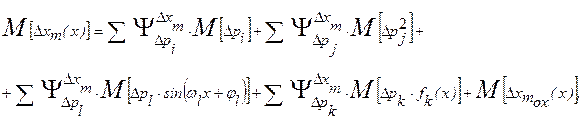
а её дисперсия:
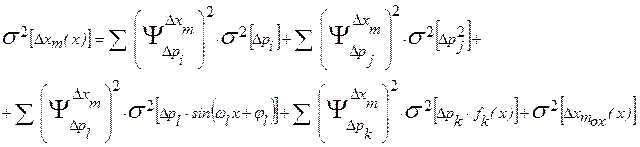
Рассмотрим отдельные составляющие, входящие в эти выражения.
1). Скалярные первичные ошибки 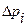 . В технических условиях на изготовление элементов измерительного звена размеры элементов задаются в виде номиналов с некоторыми допускаемыми отклонениями
. В технических условиях на изготовление элементов измерительного звена размеры элементов задаются в виде номиналов с некоторыми допускаемыми отклонениями 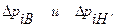
Если есть основания считать отклонений в пределах допуска распределенными нормально с вероятностью 0,95, то
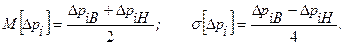
При вероятности нахождения в пределах допуска в 99,73% следует принять:
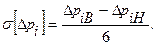
Если данных о характере распределения нет, то лучше с запасом принять равномерное распределение отклонений и тогда:
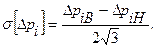
2) Квадраты скалярных первичных ошибок 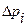 - или ошибки, пропорциональные квадрату некоторой случайной величины
- или ошибки, пропорциональные квадрату некоторой случайной величины 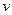 :
:
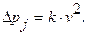
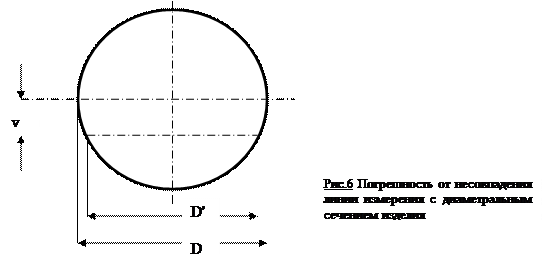
Пример: При измерении диаметра отверстия имеет место погрешность от несовпадения линии измерения и диаметрального сечения изделия (рис. 6).
Здесь 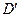 - результат измерения диаметра
- результат измерения диаметра 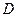 при наличии смещения
при наличии смещения 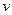 . Погрешность составляет:
. Погрешность составляет:
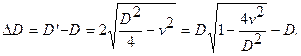
После разложения в степенной ряд по 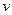 , с учетом того, что
, с учетом того, что 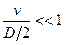 , имеем:
, имеем:
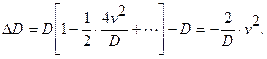
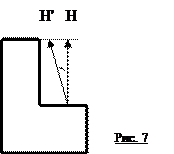
При измерении расстояния между двумя параллельными плоскостями имеет место погрешность по причине отклонения линии измерения от перпендикулярности к этим плоскостям (рис.1.7). Погрешность:
|
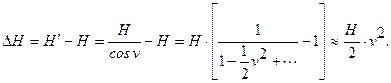
В обоих случаях погрешность пропорциональна и, даже если 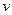 распределенj нормально, то соответствующие погрешности будут иметь совершенно другое распределение (рис. 8).
распределенj нормально, то соответствующие погрешности будут иметь совершенно другое распределение (рис. 8).
 |
 Пользуясь вероятностными методами, можно показать, что если ошибка
Пользуясь вероятностными методами, можно показать, что если ошибка  распределена нормально с нулевым математическим ожиданием и дисперсией
распределена нормально с нулевым математическим ожиданием и дисперсией 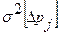 , то её квадрат имеет распределение с плотностью
, то её квадрат имеет распределение с плотностью
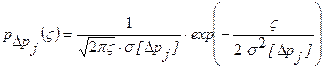 .
.
Это частный случай 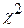 - распределения при n=1, где
- распределения при n=1, где 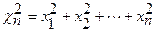 - сумма n одинаково нормально распределенных величин. При этом математическое ожидание квадрата первичной ошибки
- сумма n одинаково нормально распределенных величин. При этом математическое ожидание квадрата первичной ошибки
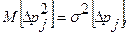
а её дисперсия
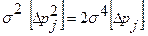
Аналогично, если первичная ошибка имеет вид 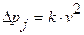 , где
, где 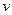 распределено нормально с дисперсией
распределено нормально с дисперсией 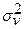 , то
, то
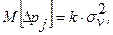
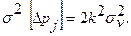
В случае измерения диаметра, номинально равного D = 10 мм при 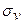 =0,1 мм, среднее значение погрешности будет составлять
=0,1 мм, среднее значение погрешности будет составлять
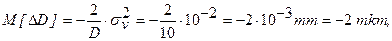
а ее дисперсия
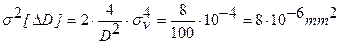
и среднее квадратическое отклонение
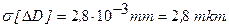
3). Векторные погрешности - это составляющие типа
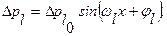
то есть периодические ошибки, являющиеся, в основном, следствием влияния различных эксцентриситетов или погрешностей зубчатых колес и передач. В этом выражении случайны амплитудное значение 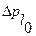 и фаза
и фаза 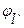
Усредненная по ансамблю реализаций средств измерения дисперсия этой погрешности составляет:
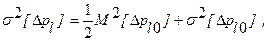
а математическое ожидание равно нулю.
Амплитудное значение погрешности 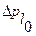 можно рассматривать как некоторый обобщенный эксцентриситет, проекции которого
можно рассматривать как некоторый обобщенный эксцентриситет, проекции которого 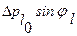 и
и 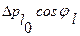 распределены нормально с одинаковыми дисперсиями и нулевыми математическими ожиданиями. В этом предположении плотность распределения амплитуд подчиняется закону Релея
распределены нормально с одинаковыми дисперсиями и нулевыми математическими ожиданиями. В этом предположении плотность распределения амплитуд подчиняется закону Релея
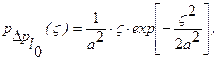
где a - некоторый параметр распределения. Математическое ожидание амплитуды составляет тогда
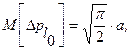
а ее дисперсия
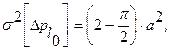
поэтому дисперсия периодической составляющей погрешности составляет:
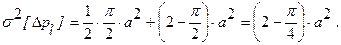
Параметр распределения 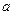 определяется по допустимым значениям амплитудного значения
определяется по допустимым значениям амплитудного значения 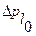 . Обычно задается только верхнее значение
. Обычно задается только верхнее значение 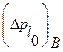 , соответствующее вероятности
, соответствующее вероятности
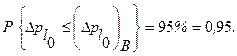
Для вычисления зависимости этой вероятности от параметра 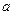 найдем выражение для интегральной функции распределения Релея:
найдем выражение для интегральной функции распределения Релея:
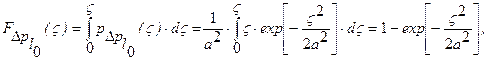
Из условия
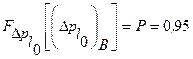
получаем
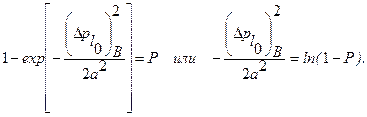
Поэтому
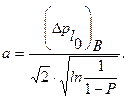
При Р=0,95
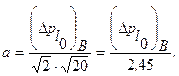
Окончательно для дисперсии периодической погрешности имеем:
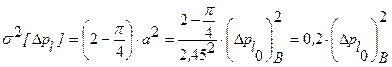
4) Нерегулярные составляющие 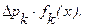 Их можно обычно рассматривать как стационарные функции входной величины или информативного параметра входного сигнала с нулевым математическим ожиданием. Нормируется обычно зона допустимых значений соответствующих первичных ошибок
Их можно обычно рассматривать как стационарные функции входной величины или информативного параметра входного сигнала с нулевым математическим ожиданием. Нормируется обычно зона допустимых значений соответствующих первичных ошибок 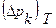 , например, отклонений формы контактирующих поверхностей, Для нормального и равномерного распределений в пределах допуска дисперсии этих отклонений составляют:
, например, отклонений формы контактирующих поверхностей, Для нормального и равномерного распределений в пределах допуска дисперсии этих отклонений составляют:
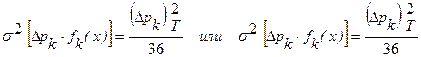
соответственно.
5). Погрешности обратного хода. Можно выделить два принципиально различных вида погрешности обратного хода.
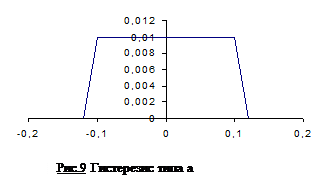 а). Погрешности типа гистерезиса; они характеризуются распределением, близким к равномерному в пределах определенной зоны (рис.1.9):
а). Погрешности типа гистерезиса; они характеризуются распределением, близким к равномерному в пределах определенной зоны (рис.1.9):
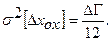
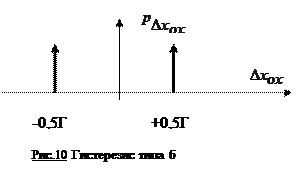 б) Погрешности типа постоянного недохода до требуемого значения выходного сигнала, например, погрешности от зазоров, влияние перекосов и т.д. Здесь возможны только два значения погрешности (рис.1.10), соответствующие возрастанию или уменьшению значения входной величины. Плотность распределения задается двум δ - импульсами. Дисперсия такой погрешности
б) Погрешности типа постоянного недохода до требуемого значения выходного сигнала, например, погрешности от зазоров, влияние перекосов и т.д. Здесь возможны только два значения погрешности (рис.1.10), соответствующие возрастанию или уменьшению значения входной величины. Плотность распределения задается двум δ - импульсами. Дисперсия такой погрешности
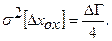
Дата добавления: 2015-11-28; просмотров: 872;
