Временные характеристики детерминированных сигналов

В качестве примеров описания временных характеристик сигналов рассмотрим четыре наиболее важных сигнала.

Единичная импульсная функция определяется как предельный случай прямоугольного импульса Рисунок5.2- Сигналы

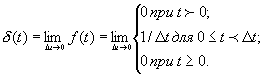
Единичная функция (скачок) определяется следующим образом :

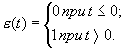
Единичная функция есть интеграл от единичной импульсной функции.

Линейно нарастающая функция, получаемая в результате интегрирования единичной функции, определяется:

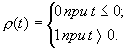
Особое место при описании сигналов занимают гармонические колебания.

В общем случае колебания по закону косинуса 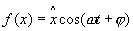можно представить в виде суммы колебаний по закону косинуса и синуса:

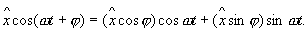
Описание гармонических колебаний можно представить в комплексной форме, используя уравнение Эйлера:

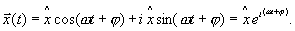
Под 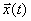в дальнейшем мы будем понимать гармонические колебания, представленные в комплексной форме.

Так как в рамках линейных операций слагаемые члены могут обрабатываться независимо, и общий результат складывается из суммы частных результатов, вычисления можно выполнить в более удобном комплексном написании. В общей системе интересующий частный результат будет получен путем отделения действительной части. Поэтому в даль­нейшем колебание по закону косинуса будет для краткости представлено в виде 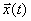= 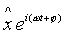без указания каждый раз, что в нем нас интересует только действительная часть.