Динамические погрешности измерений

Динамические погрешности имеют место при измерении величин, изменяющихся во времени. Аккумуляция механической, тепловой или электрической энергии в элементах измерительного устройства делает его инерционным. Инерционность проявляется в том, что показания измерительного прибора недостаточно быстро следуют за действительным изменением во времени физической величины. Построение функциональной зависимости при однофакторном эксперименте Пусть при однофакторном эксперименте имеется выборка, описывающая изменения входных параметров, и набор выходных величин (рисунок .4.1). Необходимо построить зависимость .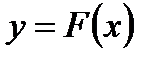

Рисунок.4.1-Входные и выходные параметры

Для анализа экспериментальных данных существует очень много способов задания этой зависимости аналитическими и численными методами. Мы отметим лишь самые распространенные из них:

1. Дальнейшая обработка может проводиться при непосредственном численном использовании массива значений .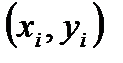

2. В случае, когда количество измерений 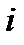не слишком велико и разброс значений 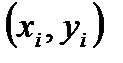мал, зависимость 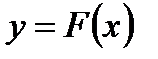может быть построена путем интерполяции (аппроксимации) через все экспериментальные точки. В этом случае проводится зависимость 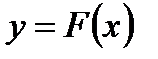через все точки с координатами 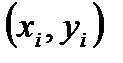. Простейший вариант проведения такой зависимости заключается в построении полинома (степенного ряда).

Пусть

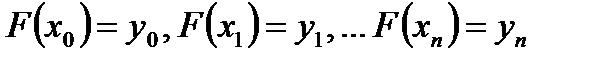. (4.3)

Интерполирующая функция

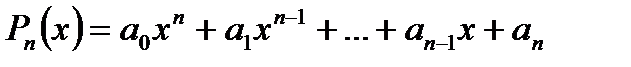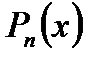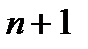. Многочлен имеет член.

Требуя выполнения условия (4.1) получим систему из 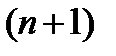уравнений с 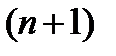неизвестными:

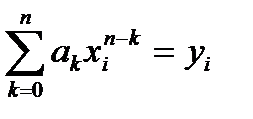, (4.4)

где каждому 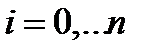соответствует свое уравнение.

Вместо решения системы уравнений (4.2) на практике используются более удобные и менее трудоемкие способы, в частности:

· интерполирование многочленом Лагранжа;

· интерполирование многочленом Ньютона.

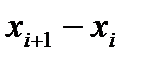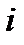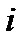Интерполяционные формулы Ньютона особенно удобны в случае равноотстоящих узлов ( одинаково для всех ) . В случае, если велико (большое число узлов), интерполяционный многочлен имеет высокую степень и оказывается неудобным для вычислений.

3. При слишком высокой степени полинома проблемы можно избежать, разбив отрезок интерполяции на несколько частей с построением для каждой из них своего интерполяционного многочлена. Такое интерполирование имеет серьезный недостаток: в точках стыка интерполяционных многочленов оказывается разрывной первая производная. На рисунке 4.2 показан простейший способ такой интерполяции экспериментальной зависимости – соединение соседних точек прямыми (многочлен степени ).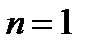

4. Если необходимо, чтобы зависимость имела непрерывные производные, пользуются сплайнами. Сплайн (от англ. spline - рейка) - функция, являющаяся алгебраическим многочленом на каждом отрезке 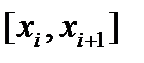, и непрерывная во всей области вместе со своими производными.

Рисунок 4.2- Сплайн - функция.

Чаще всего пользуются сплайнами третьей степени. Соответствующая зависимость показана на Рисунке 4.2-

5. При однофакторном эксперименте, когда имеются результаты многократных измерений со случайной погрешностью, проведение зависимости через все экспериментальные точки бессмысленно. Чаще всего в этом случае для построения функциональной зависимости используется (МНК).

Построение функциональной зависимости при помощи МНК.Данный метод используется тогда, когда число точек 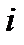(узлов) велико и построение плавной зависимости 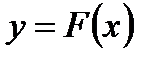, (4.5)

проходящей через все точки 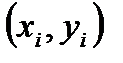невозможно из-за большого разброса значений. Функция (4.3) называется уравнением регрессии 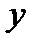на 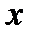. Пусть приближенная функция, описывающая 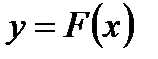зависит от трех параметров 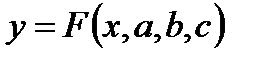. Эта функция не будет проходить через все точки с координатами 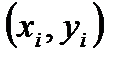, тогда можно найти сумму квадратов разностей

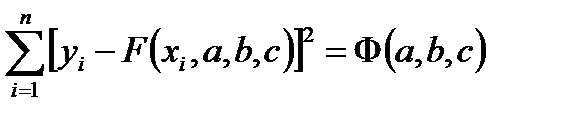. (4.6)

Задача сводится к отысканию минимума 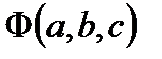, т.е. к решению системы уравнений

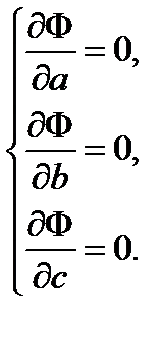
А именно

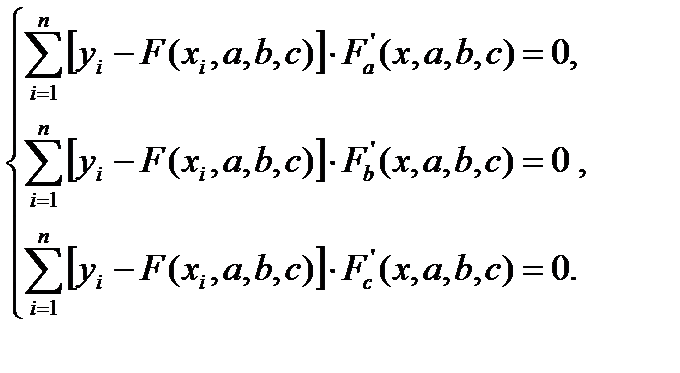(4.7)

Решив систему (4.7) относительно параметров 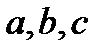, находим конкретный вид искомой функции. Приближающая (приближенная) функция может иметь любой вид: линейная зависимость, парабола, синусоида и т.д. Чаще всего используются алгебраические многочлены не выше третьего порядка. В большинстве случаев анализируется линейная регрессия, когда

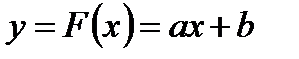. (4.8)

Главная особенность регрессионного анализа состоит в том, что регрессия 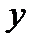на 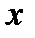не соответствует регрессии 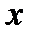на 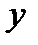(см. рис.4.3).

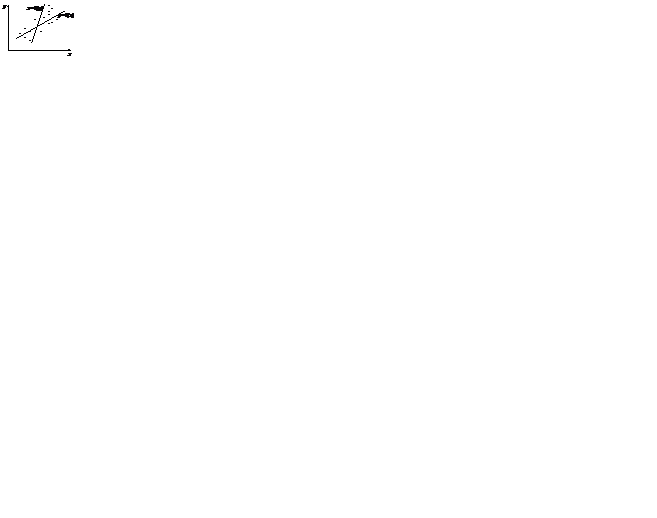
Рисунок 4.3- регрессионный анализ

Поясним это свойство регрессионных зависимостей. Пусть формула регрессии имеет вид (4.6), приведем ее обратную функцию:

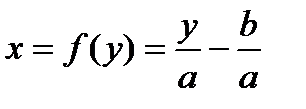. (4.9)

Обратим внимание, что в (4.7) свободный член 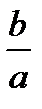зависит от коэффициента наклона 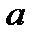прямой зависимости (4.6). При построении же регрессии, прямая проходит приблизительно через середину области, охватывающей экспериментальные точки и ее наклон определяется отношением разброса значений по осям 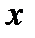и 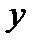(пересечение функци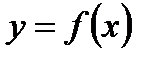й и 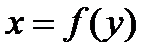находится в середине области экспериментальных значений). Таким образом, регрессия x(y), построенная по экспериментальным данным, не будет совпадать с (4.7) из-за наличия свободного члена. Графически это поясняется на рис. 4.4, где по трем экспериментальным точкам построены регрессии y(x) и x(y), которые не совпадают. Для минимизации СКО трех экспериментальных точек от прямой, зависимость должна проходить через одну из них и в середине между двумя другими точками.

Рисунок.4.4- Регрессии y(x) и x(y),

Как видно из рис.4.4, линейные регрессии, построенные из этих соображений пресекаются в центре области экспериментальных значений и имеют разный наклон. Найдем связь между коэффициентом регрессии 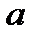и коэффициентом корреляции :

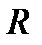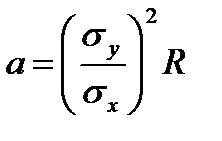, (4.10)

где 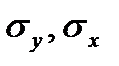- среднеквадратичные отклонения 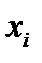и .

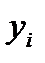Таким образом, коэффициент корреляции связан с разбросом значений по осям 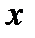, 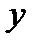и определяет возможную степень отклонения линии регрессионной зависимости по наклону. Пусть величина 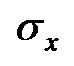фиксирована,

Рисунок 4.5-

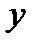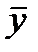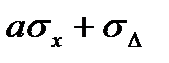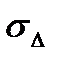тогда возможное отклонение по оси от среднего значения составляет , где - среднеквадратичное отклонение от линии регрессии (см. рис.3.6). В связи с этим, учитывая эффициент корреляции очень часто определяют как

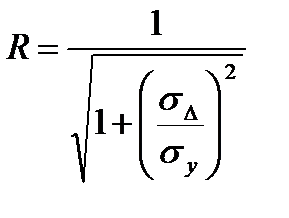, (4.11)

где 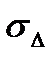- ширина полосы погрешностей по 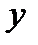; 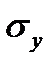- разброс значений 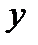, который определяется диапазоном изменения величины .

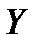Поскольку в практических случаях 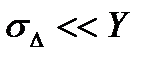, то формулу 4.11 с учетом приближенного разложения до первого члена в ряд Тейлора приводят к виду

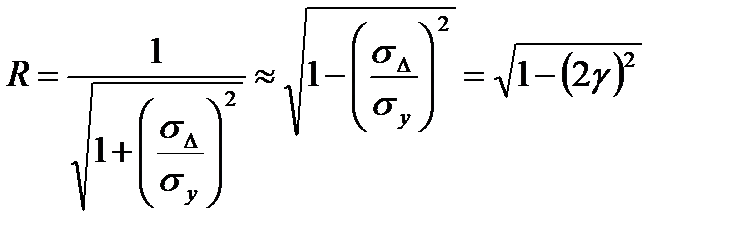. 4.12)

где 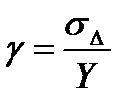- приведенная погрешность. Таким образом, в большинстве практических случаев связь между коэффициентом корреляции и приведенной погрешностью может быть установлена при помощи простейшей приближенной формулы .

Быстрая оценка коэффициента корреляции исходных данных. Быструю оценку коэффициента корреляции и погрешности исходных данных можно провести также методом медианных центров. Разобьем поле экспериментальных точек вертикальной чертой на две равные по числу точек области ( 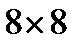точек). В левой и правой частях найдем медианные центры. Проведенная через эти медианные центры, обозначенные звездочкой, прямая 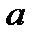- регрессия 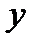на 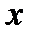. Теперь разобьем экспериментальную область на равное количество точек по вертикали горизонтальной чертой и, после нахождения соответствующих медианных центров, получим прямую 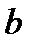- регрессию 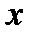на 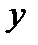. Прямые 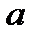и 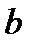совпадут только в том случае, когда коэффициент корреляции между 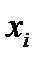и 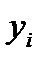равен единице, то есть .

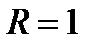По различию прямых 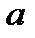и 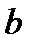можно оценить коэффициент корреляции:

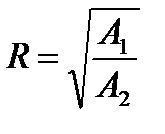, (4.13)

где 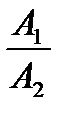определяется отношением углов их наклона. Для быстрой оценки относительной погрешности подставим величину 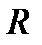из (4.13) в обращенную формулу (4.16):

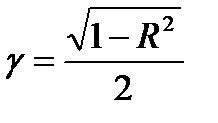. (4.16)

Таким образом, быстрая оценка коэффициента корреляции и значения относительной погрешности основывается на том, что прямые 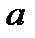и 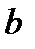обязательно проходят через точку пересечения границ О. При этом, чем выше разброс экспериментальных данных (невытянутая область), тем больше будет угол между прямым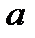и и .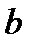

При построении регрессионных зависимостей методом медианных центров, необходимо помнить, что полученные линии регрессии в общем случае отличаются от соответствующих зависимостей, полученных при помощи МНК. Их различия будут уменьшаться при увеличении количества экспериментальных точек, если разброс экспериментальных данных подчиняется нормальному закону распределения.