Лекция 4. Линейная регрессия Линейная корреляция. Автоматическая коррекция погрешности. Динамические погрешности измерений
Линейная регрессия
В измерительной технике очень часто определяют зависимость
одной переменной у от другой 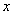 . С помощью линейной
. С помощью линейной
регрессии исследуют линейную зависимость измеряемых величин. Рассмотрим величину 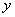 как зависимую, а величину
как зависимую, а величину 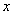 как независимую переменные. Так, например, при поверке величина, воспроизводимая мерой, является независимой, а показание поверяемого прибора - зависимой. Наиболее предпочтительна линейная зависимость, но измеренные величины
как независимую переменные. Так, например, при поверке величина, воспроизводимая мерой, является независимой, а показание поверяемого прибора - зависимой. Наиболее предпочтительна линейная зависимость, но измеренные величины 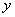 , как правило, не лежат на одной прямой. В данном случае это происходит потому, что имеется случайная погрешность измерений. При исследовании статистических процессов это обусловлено и тем, что взаимосвязь является не функциональной, а лишь статистической. Так, например, рост сыновей зависит от роста родителей, но только в статистическом смысле.
, как правило, не лежат на одной прямой. В данном случае это происходит потому, что имеется случайная погрешность измерений. При исследовании статистических процессов это обусловлено и тем, что взаимосвязь является не функциональной, а лишь статистической. Так, например, рост сыновей зависит от роста родителей, но только в статистическом смысле.
Возникает вопрос, как провести искомую прямую, называемую прямой регрессии или прямой выравнивания, через точки измерения, нанесённые на 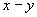 - диаграмме, или как её рассчитать. Исходя из того, что, для определённого значения независимой переменной
- диаграмме, или как её рассчитать. Исходя из того, что, для определённого значения независимой переменной 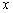 величина
величина 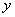 нормально распределена относительно её математического ожидания, лежащего на прямой, и что это нормальное распределение не зависит от переменной
нормально распределена относительно её математического ожидания, лежащего на прямой, и что это нормальное распределение не зависит от переменной 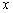 , можно применить метод наименьших квадратов. При этом рассматривают не расстояние точки измерения от прямой, а разность ординат точки измерения и прямой. Прямую линию, соответствующую минимальной сумме квадратов погрешности, с наибольшей вероятностью можно рассматривать как искомую прямую генеральной совокупности и рассчитывать по следующей формуле:
, можно применить метод наименьших квадратов. При этом рассматривают не расстояние точки измерения от прямой, а разность ординат точки измерения и прямой. Прямую линию, соответствующую минимальной сумме квадратов погрешности, с наибольшей вероятностью можно рассматривать как искомую прямую генеральной совокупности и рассчитывать по следующей формуле:
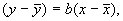 (4.1)
(4.1)
где 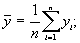
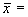
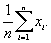
Крутизна прямой b называется коэффициентом регрессии и рассчитывается следующим образом:
b = 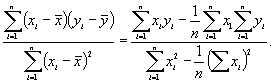 (4.2)
(4.2)
В результате получают оценку прямой линии, описывающей линейную зависимость. Здесь снова возникает проблема доверительных границ. Сначала мы рассмотрим доверительные границы для коэффициента регрессии b. Процедура решения этого вопроса состоит в следующем:
1. Выбирают доверительную вероятность Р (например, 95, 99 % ).
2. По результатам исследований (t – распределение Стьюдента) определяют 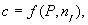 где
где 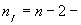 число степеней свободы.
число степеней свободы.
3. Вычисляют  :
: 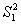 ,
, 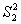 и в:
и в:
S 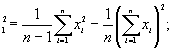 S
S 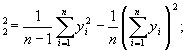 b =
b = 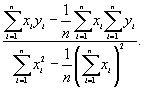
4. Определяют доверительные границы погрешности коэффициента регрессии:
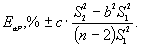
Математическое ожидание 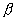 коэффициента регрессии b с доверительной вероятностью Р (%) лежит в области
коэффициента регрессии b с доверительной вероятностью Р (%) лежит в области
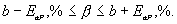
Если, доверительный интервал для коэффициента b включает величину 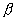 = 0, то с выбранной доверительной вероятностью нет оснований утверждать, что действительный коэффициент регрессии b отличен от нуля. В этом случае считают, что линейная зависимость не установлена с достаточной достоверностью.
= 0, то с выбранной доверительной вероятностью нет оснований утверждать, что действительный коэффициент регрессии b отличен от нуля. В этом случае считают, что линейная зависимость не установлена с достаточной достоверностью.
Дополнительная недостоверность состоит в том, что средняя величина 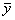 представляет собой лишь оценку соответствующего математического ожидания. Поэтому, недостоверным, является «положение» прямой линии, построенной с учетом измерений
представляет собой лишь оценку соответствующего математического ожидания. Поэтому, недостоверным, является «положение» прямой линии, построенной с учетом измерений 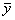 .
.
Теперь можно для каждого значения 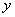 прямой линии
прямой линии 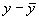 = b
= b 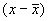
определить доверительный интервал следующим образом:
1. Выбирают доверительную вероятность Р (например, 95, 99 %).
2. По результатам, определяют
(t –распределение Стьюдента) определяют c = f (р, nf), где nf =n – 2 число степеней свободы.
3. Проводят вычисления:
S 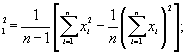 S
S 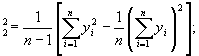 b =
b = 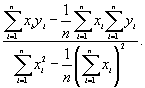
4. Определяют доверительный интервал погрешности измерений значений для разных значений 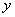 :
:
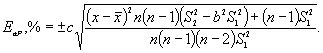 (4.3)
(4.3)
Математическое ожидание 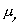 величины
величины 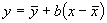 с выбранной доверительной вероятностью Р лежит в области
с выбранной доверительной вероятностью Р лежит в области
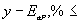
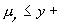
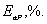
Как видно из (4.3), этот интервал зависит от 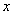 и минимален при
и минимален при 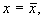 что связано с установленной выше недостоверностью коэффициента b.
что связано с установленной выше недостоверностью коэффициента b.
Если требуется проверить только то, что крутизна b значимо отличается от нуля, т.е. что имеет место существенная и линейная зависимость между 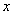 и
и 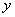 , то поступают следующим образом.
, то поступают следующим образом.
Определяют:
S 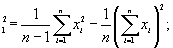 S
S 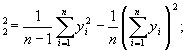 b =
b = 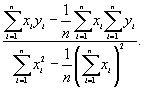
Вычисляют 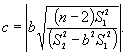
По результатам исследований (t – распределение Стьюдента) определяют Р = f (с, nf ), nf = n – 2.
Вероятность Р, представляет уровень значимости отклонения крутизны b исследуемой зависимости от прямой с b = 0.
Если уровень значимости достаточно мал (например, Р 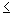 1%), то гипотеза, что
1%), то гипотеза, что 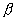 = 0, исключается. В этом случае можно предполагать, что зависимость должна быть линейной.
= 0, исключается. В этом случае можно предполагать, что зависимость должна быть линейной.
Дата добавления: 2015-12-11; просмотров: 1338;
