Вероятностные модели реальных сигналов
В качестве математической модели любого недетерминированного сигнала используется СП с подходящим образом выбранными вероятностными характеристиками.
Телефонный сигнал нельзя считать гауссовским СП, т.к. наличие пауз при разговоре приводит к заметному увеличению вероятности появления значений процесса, близких к нулю (рисунок 9.2).

Рисунок 9.2 – График плотности распределения вероятности
телефонного сигнала.
Значение математического ожидания телефонного сигнала можно считать равным нулю. Дисперсия телефонного сигнала тем больше, чем громче говорит абонент. Среднеквадратическое отклонение определяется по формуле:
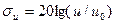 ,
,
где 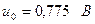 .
.
Мощность телефонного сигнала распределяется в полосе частот от 300 до 3400 Гц (рисунок 9.3).
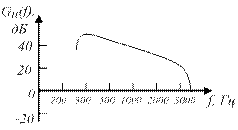
Рисунок 9.3 – Спектральная плотность мощности телефонного сигнала.
Вероятностные характеристики вещательного сигнала, если он рассматривается как СП, в значительной мере идентичны соответствующим характеристикам телефонного сигнала.
Сигнал изображения нельзя рассматривать как гауссовский СП, т.к. последний может принимать любые значения из бесконечного интервала от 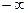 до
до 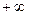 , а мгновенные значения сигнала изображения должны находиться внутри диапазона от уровня белого до уровня черного (значения вне этого диапазона не воспроизводятся на экране ТВ приемника). Математическое ожидание отлично от нуля и используется при характеризации качества изображения на экране. Дисперсия применяется сравнительно редко при описании ТВ сигналов. Спектр ТВ сигнала занимает значительную полосу частот до 6 МГц; для него характерна значительная неравномерность по частоте: мощность спектральных составляющих с повышением их частоты быстро уменьшается (рисунок 9.4).
, а мгновенные значения сигнала изображения должны находиться внутри диапазона от уровня белого до уровня черного (значения вне этого диапазона не воспроизводятся на экране ТВ приемника). Математическое ожидание отлично от нуля и используется при характеризации качества изображения на экране. Дисперсия применяется сравнительно редко при описании ТВ сигналов. Спектр ТВ сигнала занимает значительную полосу частот до 6 МГц; для него характерна значительная неравномерность по частоте: мощность спектральных составляющих с повышением их частоты быстро уменьшается (рисунок 9.4).
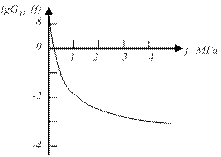
Рисунок 9.4 – Спектральная плотность мощности ТВ сигнала.
Телеграфный сигнал нельзя рассматривать как гауссовский СП, т.к. для каждого фиксированного момента времени этот сигнал может принимать лишь два значения: 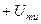 и
и 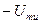 . Как правило, возможные значения он принимает с равными вероятностями (рисунок 9.4).
. Как правило, возможные значения он принимает с равными вероятностями (рисунок 9.4).
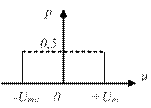
Рисунок 9.5 – Распределение вероятностей телеграфного сигнала.
Математическое ожидание телеграфного сигнала равно нулю, дисперсия – квадрату амплитуды ( 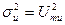 ). Ширина спектра телеграфного сигнала зависит от длительности элементарной телеграфной посылки (
). Ширина спектра телеграфного сигнала зависит от длительности элементарной телеграфной посылки ( 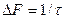 ) (рисунок 9.6).
) (рисунок 9.6).

Рисунок 9.6 – Спектральная плотность мощности телеграфного сигнала.
В качестве вероятностной модели помех различного происхождения обычно используют белый шум, т.е. процесс с равномерным спектром (спектр 1 на рисунке). Все его спектральные составляющие имеют одинаковую интенсивность (спектр имеет постоянное значение 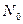 на всех частотах).
на всех частотах).

Рисунок 9.2 – Спектральные плотности мощности СП.
В качестве вероятностной модели высокочастотных модулированных сигналов при любых видах модуляции обычно применяют узкополосный процесс, т.е. процесс, ширина спектра которого 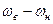 намного меньше центральной частоты (спектр 2). Средняя мощность такого процесса сосредоточена в узкой полосе частот от
намного меньше центральной частоты (спектр 2). Средняя мощность такого процесса сосредоточена в узкой полосе частот от 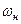 до
до 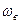 .
.
Дата добавления: 2016-01-07; просмотров: 1571;
