Нормальный закон распределения

Нормальный (гауссовский) закон распределения случайных величин очень удобен для анализа и часто встречается на практике, особенно он характерен для помех канала связи.

Плотность распределения нормальной случайной величины определяется выражением:

,

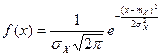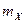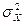где и - соответственно математическое ожидание и дисперсия гауссовской случайной величины.

График 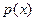имеет симметричный холмообразный вид. Центром симметрии является параметр 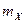. Если изменять 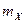, кривая распределения будет смещаться вдоль горизонтальной оси, не меняя своей формы. Параметр 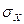характеризует форму кривой распределения. При уменьшении 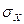максимум 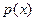увеличивается и кривая все более локализуется в окрестности точки .

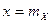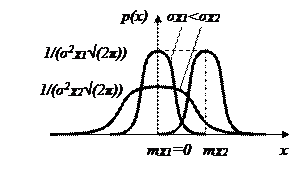
Рисунок 8.4 – Графики 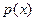случайных величин с нормальным распределением.

График 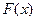имеет вид монотонной возрастающей от нуля до единицы кривой.

Рисунок 8.5 - Графики 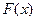случайных величин с нормальным распределением.

СИГНАЛЫ И ПОМЕХИ КАК СЛУЧАЙНЫЕ ПРОЦЕССЫ

Основные понятия

Реальные сигналы и помехи являются случайными процессами.

Случайный процесс (СП) – это случайная функция времени, т.е. такая функция времени, значение которой в любой момент времени является случайной величиной. Обозначение: .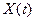

Примеры: напряжение шума на выходе линии связи, температура воздуха, ток на выходе микрофона.

Интервал наблюдения – интервал времени, на котором рассматривается СП. Обозначени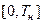е: , где 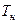- длительность интервала наблюдения.

Реализация СП– конкретный вид случайной функции времени, полученный в результате одного наблюдения над СП. Она является уже детерминированной функцией времени. Обозначени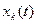е: , где 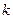- индекс, который указывает на номер наблюдения.

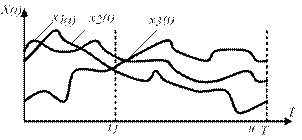
Рисунок 9.1 – Реализации СП.

Ансамбль реализаций СП – совокупность всех возможных реализаций данного СП. Обозначение: 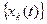. Случайность процесса проявляется в том, что до проведения наблюдения нельзя предсказать, какая именно реализация из ансамбля появится в данном испытании.

Примеры: набор сигналов, наблюдаемых одновременно на выходах многоканальной системы связи; группа сигналов, наблюдаемых одновременно на выходах идентичных генераторов шумового напряжения.

Совокупность значений всех реализаций ансамбля в произвольный момент времени представляет собой случайную величину, называемую сечением СП. Обозначение: .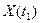

Для описания случайного процесса применяются следующие статистические характеристики:

- функция распределения вероятности;

- плотность распределения вероятности;

- математическое ожидание;

- дисперсия;

- функция корреляции;

- спектральная плотность мощности.