ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ РЯДОМ

КОТЕЛЬНИКОВА

Теорема Котельникова

Теорема Котельникова (теорема отсчетов, теорема дискретизации):

всякий непрерывный сигнал a(t) со спектром, ограниченным частотой F_max, может быть представлен последовательностью своих мгновенных значений (отсчетов), взятых через интервалы времени Δt≤1/(2F_max).

В соответствии с теоремой непрерывный сигнал с ограниченным спектром можно разложить вряд Котельникова:

,

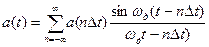где 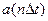- отсчет сигнала в дискретный момент времени ;

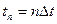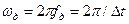- частота дискретизации;

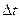- интервал дискретизации;

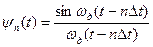- функция отсчета.

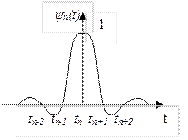
Рисунок 7.1 – Функция отсчета.

Любой реальный сигнал имеет конечную длительность. Его приближенно можно представить усеченным рядом Котельникова:

,

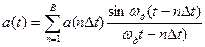где B=T_c/Δt+1=2F_maxT_c+1≈2ΔF_cT_c – общее число отсчетов для сигнала длительностью Т_с или база сигнала.

Содержание теоремы Котельникова

1. Теорема не оговаривает вид сигнала a(t), т.е. он может быть и случайным.

2. Теорема утверждает, что вся информация о сигнале a(t) содержится в его выборочных значениях a(nΔt). Следовательно, непрерывный сигнал для передачи по каналу связи может быть преобразован в дискретный по времени сигнал a_д(t). Представление непрерывного сигнала в виде последовательности его отсчетов называется дискретизацией. На практике каждый отсчет представляется импульсом величиной a(nΔt) и длительностью τ<<Δt.

Рисунок 7.2 – Дискретизация непрерывного сигнала.

3. Теорема определяет восстановление непрерывного сигнала a(t) по его отсчетам a(nΔt) на приеме: необходимо каждый отсчет умножить на функцию отсчета ψ_n(t) и произведения просуммировать.

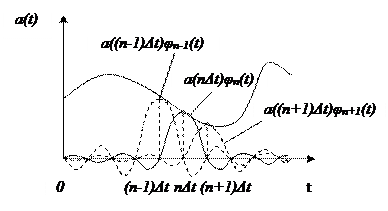
Рисунок 7.3 – Восстановление непрерывного сигнала.