Разложение в ряд Фурье ПППИ

Рассчитаем амплитудный и фазовый спектры ПППИ, имеющих амплитуду 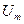, длительность 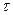, период следования 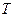и расположенных симметрично относительно начала координат (сигнал – четная функция).

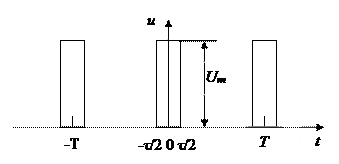
Рисунок 5.1 – Временная диаграмма ПППИ.

Сигнал на интервале одного периода можно записать:

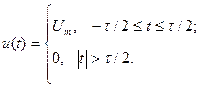
Вычисления:

,

,

,

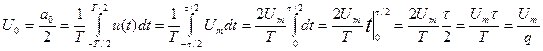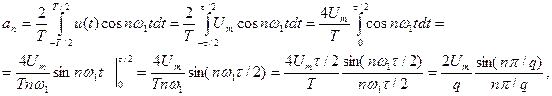
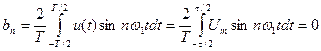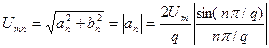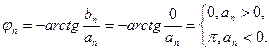
Ряд Фурье для ПППИ имеет вид: .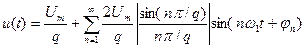

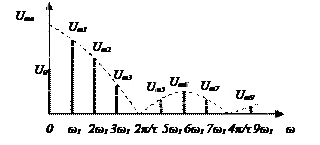
Рисунок 5.2 – Амплитудная спектральная диаграмма ПППИ.

Рисунок 5.3 – Фазовая спектральная диаграмма ПППИ.

Выводы:

- спектр ПППИ линейчатый (дискретный) (представляется набором отдельных спектральных линий), гармонический (спектральные линии находятся на одинаковом расстоянии друг от друга ω₁), убывающий (амплитуды гармоник убывают с ростом их номера), имеет лепестковую структуру (ширина каждого лепестка равна 2π/τ), неограниченный (интервал частот, в котором располагаются спектральные линии, бесконечен);

- при целочисленных скважностях частотные составляющие с частотами, кратными скважности в спектре отсутствуют (их частоты совпадают с нулями огибающей спектра амплитуд);

- с увеличением скважности амплитуды всех гармонических составляющих уменьшаются. При этом если оно связано с увеличением периода повторения Т, то спектр становится плотнее (ω₁ уменьшается), с уменьшением длительности импульса τ – становится больше ширина каждого лепестка;

- за ширину спектра ПППИ принят интервал частот, содержащий 95% энергии сигнала, (равен ширине двух первых лепестков огибающей):

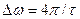или ;

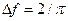- все гармоники, находящиеся в одном лепестке огибающей, имеют одинаковые фазы, равные либо 0 либо π.