ЛЕКЦИЯ 19. Двумерное преобразование Фурье

Пусть f(x₁, x₂) – функция двух переменных. По аналогии с одномерным преобразованием Фурье можно ввести двумерное преобразование Фурье:

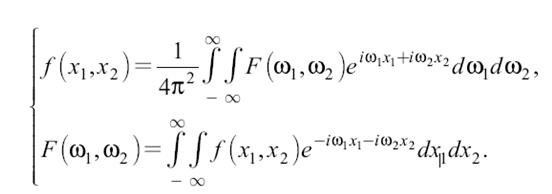
Функция при фиксированных значениях ω₁, ω₂ описывает плоскую волну в плоскости x₁, x₂ (рисунок 19.1).

Величины ω₁, ω₂ имеют смысл пространственных частот и размерность мм⁻¹, а функция F(ω₁, ω₂) определяет спектр пространственных частот. Сферическая линза способна вычислять спектр оптического сигнала (рисунок 19.2). На рисунке 19.2 введены обозначения: φ — фокусное расстояние,

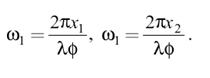
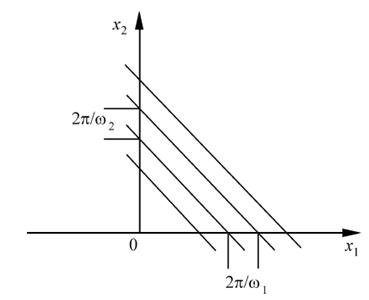
Рисунок 19.1 – К определению пространственных частот

Двумерное преобразование Фурье обладает всеми свойствами одномерного преобразования, кроме того отметим два дополнительных свойства, доказательство которых легко следует из определения двумерного преобразования Фурье.

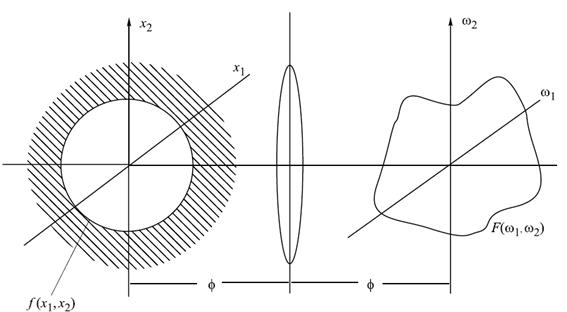
Рисунок 19.2 – Вычисление спектра оптического сигнала с использованием
сферической линзы

Факторизация. Если двумерный сигнал факторизуется,

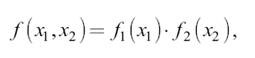
то факторизуется и его спектр:

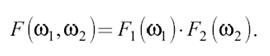
Радиальная симметрия. Если двумерный сигнал радиально-симметричен, то есть

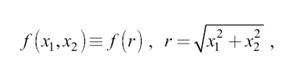
то

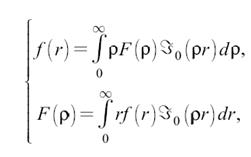
где – функция Бесселя нулевого порядка. Формулу, определяющую связь между радиально-симметричным двумерным сигналом и его пространственным спектром называют преобразованием Ганкеля.