ЛЕКЦИЯ 17. Спектры импульсов 1

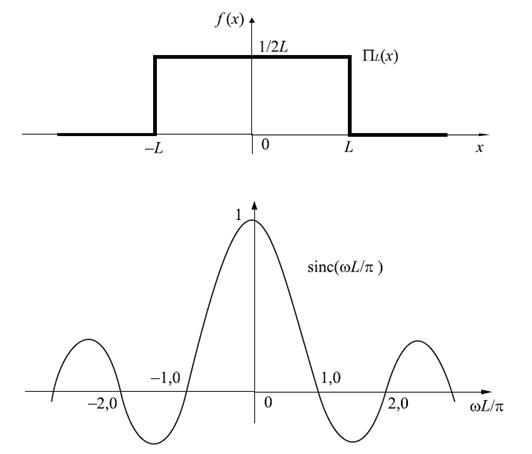
Рисунок 17.1 – Прямоугольный импульс и его спектр

Рисунок 17.2 – Сдвинутый прямоугольный импульс и его спектр

В соответствии с формулами получим

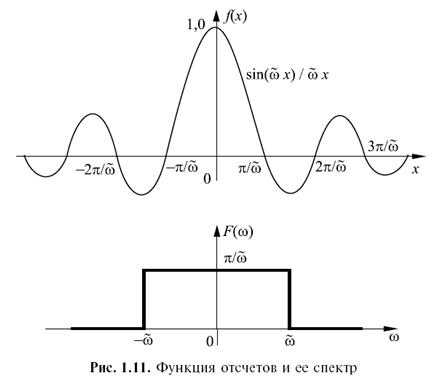
Рисунок 17.3 – Функция отсчетов и ее спектр

ЛЕКЦИЯ 18. Спектры импульсов 2

Графики меандра и его спектра приведены на рисунке 18.1.

Треугольный импульс (рисунок 18.2) можно записать в виде формулы

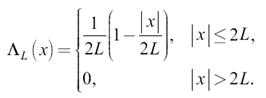
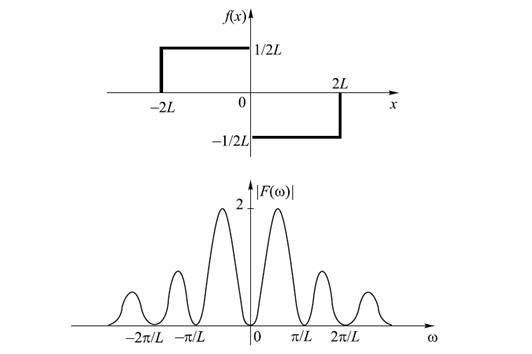
Рисунок 18.1 – Два прямоугольных импульса разной полярности и спектр их сумм

Экспоненциальный спад описывается функцией, отличной от нуля, только при x ≥ 0:

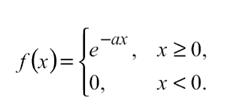
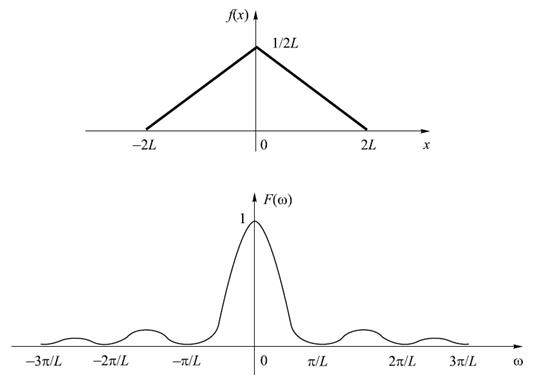
Рисунок 18.2 – Треугольный импульс и его спектр

График амплитуды и фазы экспоненциального импульса приведен на рисунке 18.3.

Рисунок 18.3 – Спектр экспоненциального импульса

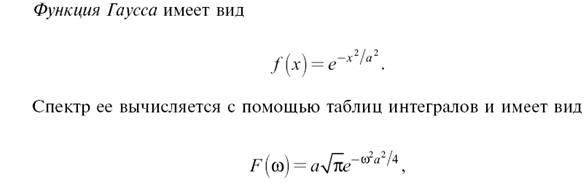
то есть также описывается гауссовой функцией, в чем и состоит двойственность рассматриваемого сигнала. Функция Гаусса представлена на рисунке 18.4а, а спектр функции – на рисунке 18.4б.

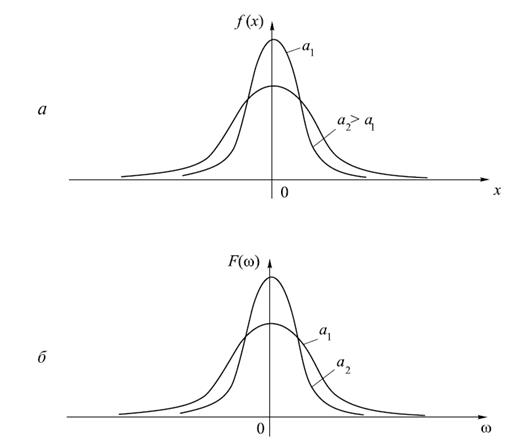
Рисунок 18.4 – Гауссов импульс (а) и его спектр (б)