Интегрирование элементарных дробей.
Определение1: дроби вида:
I. A ; II. A ; III. Mx +N ; IV. Mx + N ,
ax+b (ax+b)n (ax2 +bx + c) (ax2 +bx + c)m
где m,n- натуральные, причем m,n ≥ 2, и квадратный трехчлен ax2 +bx + c не имеют действительных корней, т.е. b2 – 4ac < 0 (D<0) – называются элементарными.
Разберем дроби.
I. ∫ A dx = A · ∫ a dx = | d(ax+b) = a dx; | = A · ∫ d(ax+b) = A · ln |ax+b| +C.
ax+b a(ax+b) a ax+b a
II. ∫ A dx = A · ∫ (ax+b)-n d(ax+b) = A · (ax+b)-n+1 = A + C;
(ax+b)n a a (1-n ) a·(1-n) ·(ax+b)n-1
III. ∫ Mx + N dx;
ax2 +bx + c
Рассмотрим сначала Y = 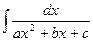 =
= 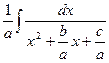 =
= 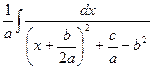 =
=
= 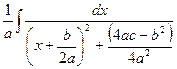 = │т.к. b2 – 4ac <0 (по условию), то 4ac – b2 >0, тогда
= │т.к. b2 – 4ac <0 (по условию), то 4ac – b2 >0, тогда
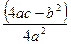 >0; обозначим
>0; обозначим 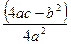 = k2 ;│=
= k2 ;│= 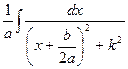 =
=
=│ Пусть 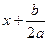 = t, dx=dt; │ =
= t, dx=dt; │ = 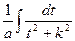 =
= 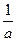 arctg(
arctg( 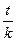 ) =
) = 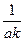 ·arctg
·arctg 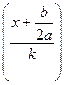 +C;
+C;
Y = 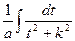
Рассмотрим искомый интеграл:
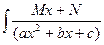 dx =
dx = 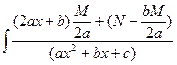 dx =
dx = 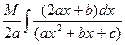 +
+
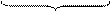 +
+ 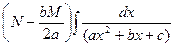 =
= 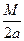 ∫ (ax2 +bx + c)–m d(ax2 +bx + c) + (N –
∫ (ax2 +bx + c)–m d(ax2 +bx + c) + (N – 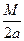 ) ·Y =
) ·Y =
Y
= 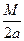 ·ln|ax2 +bx + c| + (N –
·ln|ax2 +bx + c| + (N – 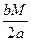 )
) 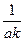 arctg
arctg 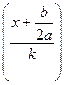 + C.
+ C.
Пример:
∫ 7x – 2 dx = ∫ (6x-5)·7/6 – 2 + 35/6 dx = 7/6 · ∫ (6x – 5) dx + ∫ 35/6 – 2 dx=
3x2 – 5x+4 3x2 – 5x+4 3x2 – 5x+4 3x2 – 5x+4
= 7/6 ·∫ d(3x2 –5x+4) + 23/18 ·∫ dx = 7/6 ln |3x2 –5x+4| +23/18 ·∫ d (x – 5/6) =
3x2 – 5x+4 x2 –5/3·x+4/3 (x–5/6)2 +23/36
= 7/6 ln |3x2 – 5x+4| + 23/18 ·1/( 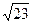 / 6) ·arctg (x – 5/6) + C = 7/6 ln |3x2 – 5x+4| +
/ 6) ·arctg (x – 5/6) + C = 7/6 ln |3x2 – 5x+4| + 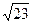 /3 ·
/3 ·
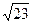 /6
/6
·arctg (6x – 5) + C.
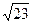
IV. 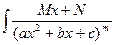 dx =
dx = 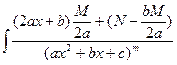 =
= 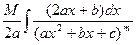 +
+
+ 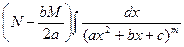 =
= 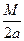 ∫ (ax2 +bx + c)–m d(ax2 +bx + c) + (N –
∫ (ax2 +bx + c)–m d(ax2 +bx + c) + (N – 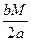 ) ·
) ·
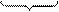 ·
· 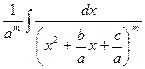 =
= 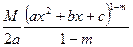 + (N –
+ (N – 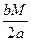 )
) 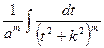 ) = |см. пример 3|
) = |см. пример 3|
Ym
= 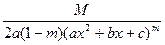 + (N –
+ (N – 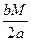 )
) 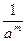 Ym .
Ym .
Отдельно вычислим Ym.
Ym = ∫ dt = 1 ·∫ (t2+k2 ) – t2 dt = 1 ·∫ dt – 1 ·∫ t2 dt = 1 ·Ym-1 –
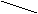
 (t2+k2)m k2 (t2+k2)m k2 (t2+k2)m-1 k2 (t2+k2)m k2
(t2+k2)m k2 (t2+k2)m k2 (t2+k2)m-1 k2 (t2+k2)m k2
Ym-1
– 1 ·∫ t2 dt = | U=t, dU = dt; dV = t dt ; V =1/2 ·∫ (t2+k2)–m d(t2+k2) =
k2 (t2+k2)m (t2+k2)m
= 1 · (t2+k2)–m+1 ; | ;
2 – m+1
Ym = 1 ·Ym-1 – 1 ·( t – ∫ dt ) = 1 ·Ym-1 –
k2k22(1-m)(t2+k2)m-12(1-m)(t2+k2)m-1k2
– t + 1 ;
 2k2(1-m)(t2+k2)m-1 2k2(1-m)(t2+k2)m-1
2k2(1-m)(t2+k2)m-1 2k2(1-m)(t2+k2)m-1
Ym-1
Ym = t + 1 ·Ym-1 ·(1 + 1 ) = t + 1 Ym-1 ·
2k2(m –1)(t2+k2)m-1 k2 2(1-m) 2k2(m –1)(t2+k2)m-1 k2
·3 – 2m ;
2(1 – m)
Получили: Ym = t + 1 ·3 – 2m ·Ym-1.
2k2(m –1)(t2+k2)m-1 k2 2(1 – m)
Пример:
∫ 2x – 4 dx = ∫ (2x+2) – 6 dx = ∫ (x2 + 2x +5)–2 · (2x+2) dx – 6 ·∫ dx =
(x2 + 2x +5)2 (x2 + 2x +5)2 ((x+1)2+4)2
= | x+1=t; | = ∫ (x2 + 2x +5)–2 d(x2 + 2x +5) – 6 ·∫ dt = (x2 + 2x +5)–1 – 6 ·∫ (4+t2) – t2 dt =
(t2 + 4)2 -1 4 (t2+4)2
= – 1 – 3 ∫ dt + 3 ∫ t2 dt = | U = t; dU=dt; dV= t dt ;
x2 + 2x +5 4 t2 + 4 2 (t2 + 4)2 (t2 + 4)2
V =1/2 ·∫ (t2 + 4)–2 d(t2 + 4) = –1/2 (t2 + 4)–1 = –1/2 – 1 ; | = – 1 – 3 · Y1 +
t2 + 4 x2 + 2x +5 2
+ 3 ·( t – ∫– dt ) = – 1 – 3 · Y1 – 3t + 3 ·Y1 = – 1 -
2 –2(t2 + 4) 2(t2 + 4) x2 + 2x +5 2 4(t2 + 4) 4 x2 + 2x +5
– 3t + 3 Y1 = – 1 – 3(x+1) + 3 ·1 ·arctg ( x+1 ) + C.
4(t2 + 4) x2 + 2x +5 4(x2 + 2x +5) 4 2 2
Дата добавления: 2015-12-16; просмотров: 608;
