Несобственные интегралы.

Несобственными интегралами называют:

1) интегралы с бесконечно верхними или нижними пределами интегрирования.

2) Интегралы от неограниченных функций на отрезке [a,b] или интегралы от разрывных функций на отрезке [a,b].

Рассмотрим 1):

Пусть функция ƒ(х) непрерывна на [a, +∞). Если существует 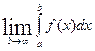, то он называется несобственным интеграломс бесконечным верхним пределом и обозначается .

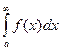y y =ƒ(х)

0 a x

Итак, по определению:

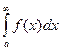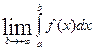= , если этот предел существует, то интеграл называется сходящимся, в противном случае расходящимся.

Аналогично

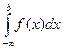= , если этот предел существует, то интеграл называется сходящимся,в противном случае расходящимся.

Интеграл вида: 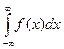= |по свойству 5 определенного интеграла| = +

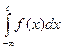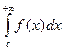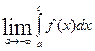+ = + - интеграл сходится.

Пример: Вычислить ;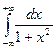

Тогда, ƒ(х) = ;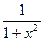

y

1

01x

= + = + = +

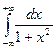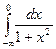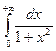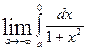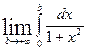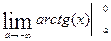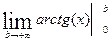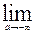+ = (0 – arctg(a)) + 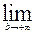(arctg(b) – 0) = -(- 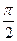) + 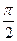= 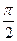+ 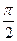= π.

Рассмотрим 2): несобственные интегралы от разрывных функций.

Пусть функция ƒ(х) непрерывна на отрезке [a,c).

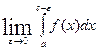Если существует , то y

он называется несобственным интегралом

от неограниченной функции в точке с и

обозначается .

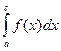a c-ε c x

Пусть функция ƒ(х) непрерывна на отрезке (c,b].

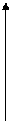y = .

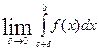c c+δ b x

Пусть функция ƒ(х) непрерывна на отрезке [a,b], кроме точки c, a<c<b, тогда

= + = + .

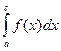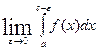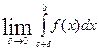y Если оба эти предела существуют, то несобственный

интеграл называется сходящимся, а если один из

пределов не существует, то расходящимся.

a c b x

Пример: ;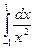

х = 0 - точка разрыва; ƒ(х) = ;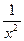

y

0-ε 0+δ

-1 0 1 x

= + = + = + =

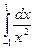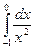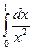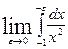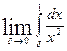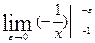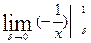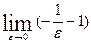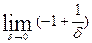= + = ∞ + ∞ = ∞, значит интеграл расходится.

Раздел III.