Интеграл с переменным верхним пределом.
Функция y = ƒ(х) непрерывна на отрезке [a,b], х 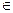 [a, b];
[a, b];
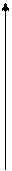 Рассмотрим интеграл
Рассмотрим интеграл 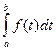 - интеграл зависит от х, т.е. является функцией от х.
- интеграл зависит от х, т.е. является функцией от х.
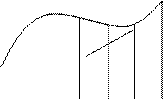
y
y = ƒ(х)
 |
 ΔΦ
ΔΦ
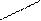

x+Δx 
0 a x ζ b x
Обозначим интеграл Φ(х). Переменную интегрируемую обозначаем через t, чтобы не спутать с верхним пределом х.
Теорема: Производная от интеграла с переменным верхним пределом от непрерывной функции по верхнему пределу равна подынтегральной функции, с заменой переменной, интегрируемая на верхней предел, т.е.
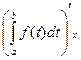 = ƒ(х);
= ƒ(х);
Доказательство.
Дадим х приращение Δх, тогда Φ(х), получим приращение ΔΦ=Φ(х+ Δх) - Φ(х) =
= 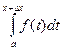 –
– 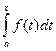 = | по свойству 4| =
= | по свойству 4| = 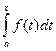 +
+ 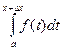 –
– 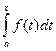 = { по теореме о среднем} = ƒ (ζ)(x + Δх –x) = ƒ(ζ)Δх.
= { по теореме о среднем} = ƒ (ζ)(x + Δх –x) = ƒ(ζ)Δх.
Итак, получили, что ΔΦ = ƒ(ζ)Δх.
Разделим обе части на Δх, получим:
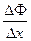 = ƒ(ζ), где ζ лежит между х и х + Δх.
= ƒ(ζ), где ζ лежит между х и х + Δх.
Перейдем к пределу.




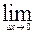 (
( 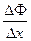 ) =
) = 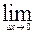 ƒ(ζ); х ζ х+Δх
ƒ(ζ); х ζ х+Δх
при Δх→0 (х+ Δх) →х, а ζ →х;
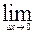 (
( 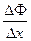 ) = ƒ(х). Но этот предел есть производная от Φ'(х)
) = ƒ(х). Но этот предел есть производная от Φ'(х)
Φ'(х) = ƒ(х);
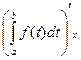 = ƒ(х);
= ƒ(х);
Замечание1 из доказательства видно, что функция Φ(х) является первообразной для функции ƒ(х), а значит попутно доказали теорему.
Замечание2:
Если функция непрерывна на [a,b] , то на этом отрезке существует первообразная функции.
Интеграл с переменным верхним пределом и неопределенный интеграл связаны следующим соотношением:
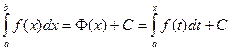 .
.
Дата добавления: 2015-12-16; просмотров: 600;
