Вычисление многомерных интегралов методом Монте–Карло.

Пусть необходимо вычислить

.

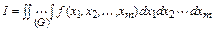Заключим область интегрирования 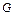внутрь 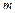-мерного параллепипеда со сторонами 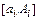, т. е. 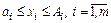. Сделаем замену переменных

.

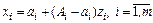Тогда 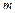-мерный параллепипед преобразуется в 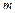-мерный единичный куб, т. к.

.

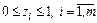Область 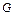преобразуется в область 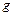, заключенную внутри 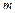-мерного единичного куба (рис. 9.3).

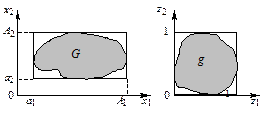
Рис. 9.3. Преобразование области интегрирования в двумерном случае

С учетом преобразования переменных

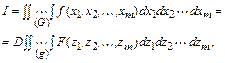
где .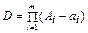

По теореме о среднем можно положить

,

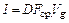где 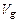– объем области интегрирования 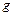, 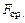– усредненное значение функции 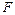в области .

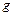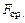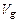Для вычисления и воспользуемся методом статистических испытаний (методом Монте–Карло). Пусть мы умеем строить случайные числа, распределенные в интервале 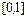по равномерному закону. Обозначим через 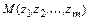случайную точку 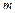-мерного пространства, координаты которой 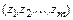являются независимыми случайными величинами, распределенными в интервале 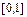по равномерному закону. Используя датчик случайных чисел, сформируем 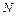случайных точек .

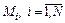Разобьем это множество точек на два подмножества:

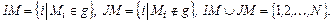
Пусть подмножество 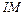содержит 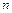элементов, т. е. 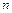точек 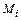из общего числа 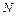принадлежат области интегрирования 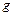. Тогда

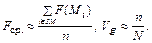
Следовательно,

.

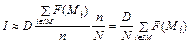Окончательное расчетное соотношение метода Монте–Карло для вычисления определенных интегралов принимает вид

.

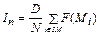Методом Монте-Карло пользуются в тех случаях, когда достаточен невысокий порядок точности.