Анализ многомерных АС.

Анализ МАС вновь сводится к решению двуединой задачи: оценке устойчивости и качества. Как известно, для одномерных систем оценка качества сводилась к определению динамических характеристик системы и по ним определение прямых и косвенных показателей качества. Для многомерных систем появляются свои специфические оценки качества, обусловленные особенностями структуры МАС. Это прежде всего управляемость, наблюдаемость и идентифицируемость.

9.1.Управляемость и наблюдаемость многомерных АС

Понятие управляемости связано с возможностью перевода МАС под воздействием управления из одного состояния в другое. Понятие же наблюдаемости - с возможностью восстановления полного вектора состояния системы по вектору измерения, в общем случае не совпадающего с вектором состояния. Не смотря на почти столетнюю историю теории автоматического управления как науки, данные понятия были четко определены лишь в начале 60-х годов американским ученым Р.Калманом.

Многомерная АС называется управляемой, если существует некоторое управление (входной сигнал) Y(t),переводящий систему из любого начального состояния, характеризуемого вектором X(t₀) в любое конечное состояние X(t_k) за конечное время Dt=t_k-t₀.

Очевидно, что необходимым условием управляемости системы является возможность с помощью вектора входных сигналов Y(t) влиять на все координаты вектора состояния X(t).

Пример: уравнение состояния МАС имеет вид

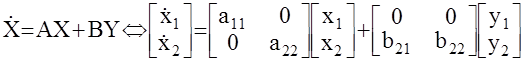
или в скалярном виде .

Как видим, в данной системе ни одно из задающих воздействий y₁ и у₂ не влияет на изменение координаты х₁. Следовательно, достигнуть любого конечного состояния 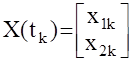невозможно. Поэтому данная АС относится к классу неуправляемых.. Однако часто по виду уравнения состояния невозможно сказать управляема ли система или нет. Естественно найти некоторый критерий, подобный критериям устойчивости, который бы позволил представить понятие управляемости в виде математического соотношения.

Критерий управляемости Калмана.

Многомерная АС 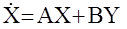размерности n управляема тогда и только тогда, когда блочная матрица 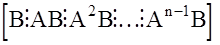имеет ранг равный n :

rank .

Например: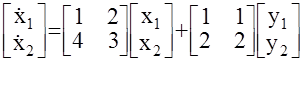

Размерность данной МАС n=2. Сформируем блочную матрицу

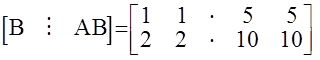Ранг этой матрицы равен 1, так как все окаймляющие миноры второго порядка равны 0. Следовательно, данная МАС неуправляема, хотя по виду ее уравнения состояния этого сказать нельзя.

Рассмотрим теперь задачу о наблюдаемости МАС. Данная задача имеет место в том случае, когда вектор состояния системы не полностью доступен для непосредственного измерения(наблюдения). Например, в задачах так называемого траекторного управления ЛА, появляется проблема контроля угла наклона траектории Q, который недоступен для непосредственного измерения (нет таких датчиков). Возникает вопрос о восстановлении данного параметра по показателям других датчиков. Математически данную проблему можно представить так : 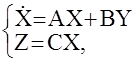То есть к уравнению состояния МАС добавляется уравнение измерительной системы :Z-вектор измерения размерности r £ n, С- матрица измерений r ´ n.Тогда понятие наблюдаемости можно сформулировать так:

Многомерная АС называется наблюдаемой, если ее вектор состояния можно непосредственно или косвенно восстановить по вектору измерения.

Соответствующий критерий наблюдаемости, также сформулированный Калманом определяется так.

Многомерная АС 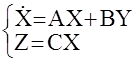наблюдаема тогда и только тогда, когда блочная матрица 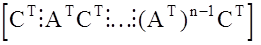имеет ранг равный n, то еcть

rank .

Пример: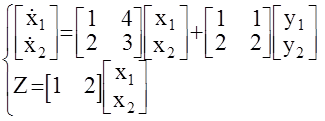

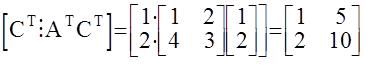Ранг этой матрицы равен 1, так как единственный минор второго порядка равен 0, следовательно данная МАС ненаблюдаема.

9.2.Идентифицируемость многомерных АС.

Рассмотрим МАС, описываемую системой матричных уравнений

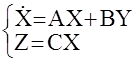На практике часто возникает проблема нахождения параметров (коэффициентов) матриц А,В и С. Эта проблема получила название задачи параметрической идентификации объектов. Более подробно она будет изучена в разделе V, здесь же только остановимся на условиях идентифицируемости рассматриваемой МАС.

Параметрическая идентифицируемость представляет собой возможность определения параметров математической модели системы по результатам измерения ее входных U и выходных Z координат. Аналитическте условия идентифицируемости в наиболее полном виде были получены в трудах А.А.Красовского и могут быть сформулированы для линейных стационарных систем в следующем виде.

Многомерная АС 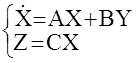идентифицируема тогда и только тогда, когда выполняются условия: rank 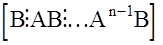=n; rank 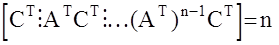; rank ,

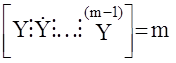m- размерность вектора Y.

Первые два условия представляют известные требования к управляемости и наблюдаемости МАС. Последнее условие определяет требования к входным сигналам при идентификации. Например, если m=1, то это условие просто означает неравенство нулю входного сигнала. При m³ 2 добавляются условия существования производных до (m-1) порядка включительно и различности управляющих сигналов для различных входов. В литературе часто последнее условие интерпретируется как условие ,,богатства’’ входного сигнала или ,,информативности маневра’’.

Таким образом, успешная идентификация определяется не только внутренними свойствами (связями) самого объекта (управляемость и наблюдаемость) но и достаточно жесткими требованиями к виду входного сигнала.

9.3.Фундаментальная матрица многомерной АС.

Рассмотрим уравнение состояния МАС

,

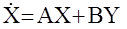A -матрица состояния n´n;

U-вектор входных сигналов (управления) m´1.

Решение данного матричного уравнения может быть определено так

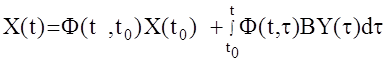. Данное выражение называется формулой Коши для МАС. Здесь Ф(t,t₀)-фундаментальная матрица решений системы, удовлетворяющая однородному матричному дифференциальному уравнению : 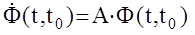при начальных условиях 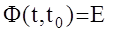Решением этого уравнения является так называемая матричная экспонента 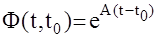где А-матрица (n´n) cостояния исходной системы.

Проверка: ,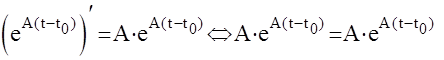

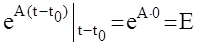, что и требовалось доказать.

Свойства фундаментальной матрицы.

1.Разложение в ряд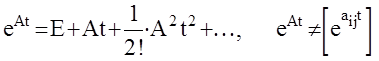

2.Матричная экспонента перестановочна с матрицей А

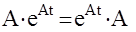
3.Дифференцирование и интегрирование

;

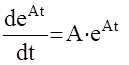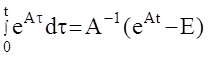
4.Если все корни характеристического полинома 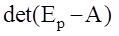имеют отрицательные части, то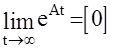

9.4.Временные характеристики МАС.

К временным характеристикам относятся весовая и переходная функции, то есть реакции МАС на единичный импульс d(t) и единичный скачок 1(t) при нулевых начальных условиях. Причем отметим, что d(t) и 1(t) есть функции скалярные, а соответствующие реакции G(t) и H(t) представляют собой матрицы (n´m) каждый элемент которых есть g_ij(t) либо h_ij(t)- скалярные реакции i-той координаты состояния на j-тый входной сигнал.(i=1,2,...n; j=1,2,...m).

Определим теперь эти функции воспользовавшись формулой Коши, при нулевых начальных условиях.

Весовая функция МАС =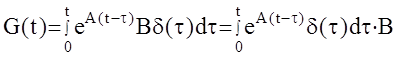

е^At B ( ,,фильтрующее’’ свойство d-функции ).Таким образом, 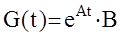- матрица размерности n´m.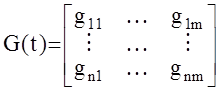

Переходная функция 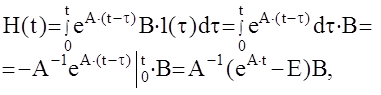т.о.

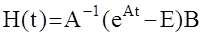Видим, что H(t)- также матрица размерности (n´m). Продифференцируем: 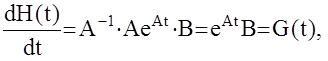что соответствует установленным ранее теоретическим положениям.Таким образом, для МАС удалось получить точные аналитические выражения для временных характеристик и пользоваться ими при определении рассмотренных ранее прямых и косвенных показателей качества.

9.5.Частотные характеристики многомерных АС.

Как и для одномерных систем амплитудно-фазовая характеристика МАС может быть получена из матричной передаточной функции заменой переменной Лапласа р на jw. 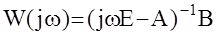- матрица размерности n´m .

Очевидно, что нахождение АФЧХ по этой формуле требует оперирования с комплексными числами (при обращении), что на практике является достаточно затруднительной задачей. Возникает вопрос- как обойти указанные трудности?

Рассмотрим реакцию МАС в установившемся режиме на скалярный гармонический сигнал вида 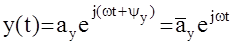, где

Реакцию МАС будем искать также в виде гармонического сигнала (только уже матрицы n´m)

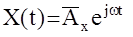, где 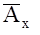-матрица n´m комплексных амплитуд выходного сигнала, каждый элемент которой определяется так 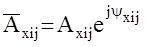Любая комплексная матрица ( в данном случае 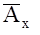) может быть представлена в виде 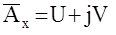, где U,V- матрицы вещественных и мнимых частотных характеристик.Определим эти матрицы, подставив выражения для y(t) иX(t) в уравнение состояние системы: .

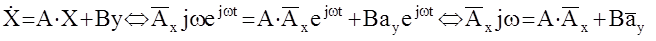Подставим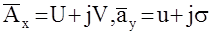

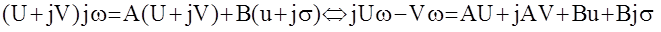
Из условия равенства двух комплексных выражений имеем :

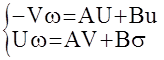. Решая данную систему (обычных некомплексных) уравнений, можно определить матрицы вещественных U и мнимых V частотных характеристик. По этим характеристикам определяются все другие частотные характеристики МАС:

АФЧХ: 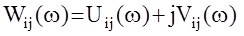i=1,...,n; j=1,2,...m

АЧХ:

ФЧХ: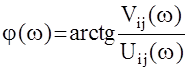

Частотные характеристики позволяют оценить влияние частоты j-того входного сигнала на амплитуду и фазу i-того выхода.