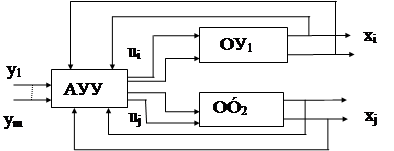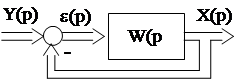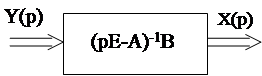Математические модели многомерных автоматических систем

8.1Понятие о системах с несколькими регулируемыми параметрами

В предыдущих разделах изучались одномерные системы. Они могли иметь сложную структуру, много внутренних контуров, но в них всегда имелась одна выходная регулируемая величина: обычно либо х(t), либо e(t) и одно задающее воздействие у(t) (хотя возмущающих воздействий может быть несколько f₁(t),f₂(t),...).Однако на практике часто возникает потребность в одновременном регулировании не­скольких выходных величин при нескольких входных воздействиях. Так в системах автоматического управления ЛА требуется обеспечи­вать одновременное управление углами тангажа J, крена g и рыскания y за счет отклонения соответствующих рулевых поверхно­стей: руля высоты d_в, элеронов d_э и руля направления d_н.

Системы, в которых имеются две и более выходных регулируе­мых величин и входных задающих воздействий, называются многомерными или многосвязными автоматическими системами (МАС).

Рассмотрим особенности, которые отличают многомерные системы от одномерных. МАС могут включать в себя один объект управления с несколькими регулирующими органами и несколькими регулируемыми величинами.Например: самолет, авиационный двигатель, генератор и т.п.

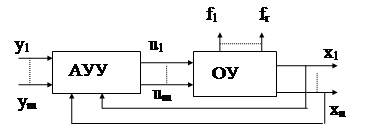
Но могут быть МАС с несколькими объектами управления, объе­диненными единым управляющим устройством, в котором организу­ется требуемая взаимосвязь между регулируемыми величинами всех объектов. Например, система электроснабжения ЛА,системы управления строем самолетов и т.д.

Взаимосвязи, определяющие многомерность системы, могут быть различными. Их можно разделить на две категории: а) внутренние связи и б) внешние связи. Внутренние связи- это связи, физически существующие между выход­ными величинами в самом объекте. Математически эти связи заложены в уравнениях динамики объекта. Внешние связи- это связи, организуемые в управляющем устройстве или между управляющими устройствами. Задача внешних связей, создающихся обычно при синтезе АС, может быть двоякой. В одних случаях требуется организовать определенные взаимосвязи между регулируемыми величинами. В других случаях, на­оборот, требуется ликвидировать внутренние связи существующие в объекте, то есть обеспечить автономность (независимость) управления по разным координатам.

Так как входные и выходные сигналы МАС состоят из несколь­ких переменных, то наиболее удобной формой их представления явля­ется векторная форма.

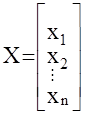
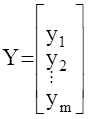-вектор выходных воздействий; - вектор вход­ных воздействий; 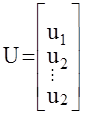- вектор управляющих воздействий.

Соответствующие обозначения на структурных схемах следующие:

Математический аппарат исследования многомерных АС основан на теории матриц.

8.2Основные правила преобразования матричных уравнений.

Определим основные правила действий над матрицами.

Матрицей называется упорядоченная таблица чисел или функций, по­ложение которых в этой таблице задается номером строки и номером столбца.

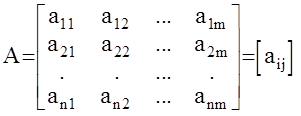-эта таблица (матрица) характеризуется числовыми характеристиками, к важнейшим из которых относятся:

1. Размерность матрицы dimA=n ´ m, где n- число строк, m- число столбцов.

2. Определитель матрицы (только при m = n)

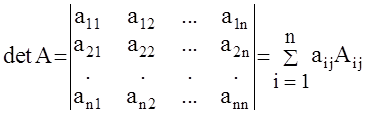где A_ij- алгеброическое дополнение элемента a_ij, - это определитель, получающийся из исходного путем вычеркивания i-той строки и j- того столбца и умноженного на (-1)^i+j

3. Минором к-того порядка М_к матрицы А называется определитель, получающийся на пересечении любых ее к строк и к столбцов.

Главным диагональным минором матрицы А называется определитель, стоящий на пересечении ее к последовательных строк, начиная с первой и к соответствующих столбцов.

4. Ранг матрицы- это порядок наивысшего отличного от нуля миноров этой матрицы .

Например: 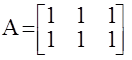, rank A=1, потому что все М₂=0 (метод окаймляющих миноров).

Над матрицами можно производить различные операции, к основным из них относятся:

1. Сложение. Суммой двух матриц А и В одинаковой размерности называется такая третья матрица С, каждый элемент которой есть сумма соответствующих элементов матриц А и В:

С=А+ВÛ с_ij=a_ij+b_ij, i=1,...n, j=1,...m

2. Умножение. Произведением двух матриц А и В называется такая матрица С, каждый элемент которой равен сумме произведений элементов строки первой матрицы на соответствующие элементы столбца второй матрицы.

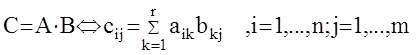
Из этого определения в частности следует, что для того чтобы это произведение существовало необходимо, чтобы число столбцов первой матрицы r совпадало с числом строк второй матрицы. Кроме того, операция умножения матриц некоммутативна, то есть А×В ¹ В×А.

3. Транспонирование

Матрица А^Т называется транспонированной по отношению к матрице А, если строки матрицы А^Т являются столбцами матрицы А и наоборот.

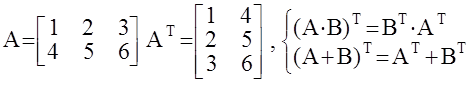
4. Обращение (только для квадратных матриц)

Матрица А^-1 называется обратной по отношению к матрице А, если она удовлетворяет условию

А×А^-1 = А^-1×А = Е,

где 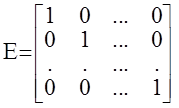- единичная матрица.

Операция обращения обычно осуществляется по формуле:

.

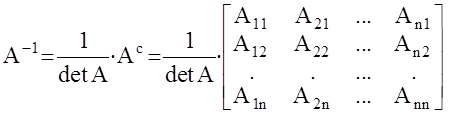А^с - союзная или присоединённая матрица, состоящая из алгебраических дополнений элементов транспонированной матрицы А.

Например: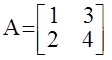

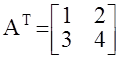
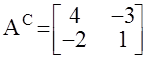
detA= 4 - 6 = - 2

Проверка: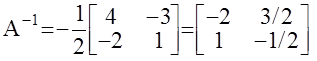

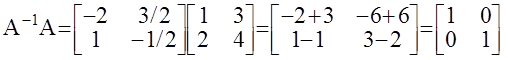
5. Умножить матрицу на число, разделить ее на число, продифференцировать или проинтегрировать - это значит проделать соответствующие операции над всеми элементами матрицы.

8.3.Матричная передаточная функция.

Рассмотрим многомерную АС описываемую системой n линейных дифференциальных уравнений с постоянными коэффициентами m входными и n выходными сигналами, приведенную к форме Коши.

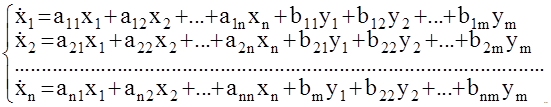
Используя аппарат теории матриц данную систему можно записать так:

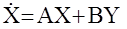
Данное уравнение получило название уравнение состояния МАС.

Здесь Х = 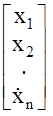-вектор, характеризующий состояние многомерной АС, - вектор состояния, его порядок n называется порядком системы;

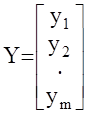- вектор входных воздействий или вектор управления (часто обозначается как вектор U );

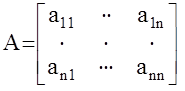- матрица n´n состояния объекта (динамическая матрица объекта);

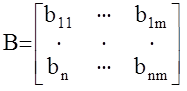- матрица n´m эффективности управлений.

Применим к данному матричному уравнению преобразование Лапласа при нулевых начальных условиях:

рХ(р)=АХ(р)+ВY(р) Û (pE-A)X(р)=BY(р)Þ

W(р)=(pE-A)^-1B.

Данное выражение называется матричной передаточной функцией многомерной АС

Матричная передаточная функция W(p) представляет собой прямоугольную матрицу размерности n´m. Каждый элемент этой матрицы- есть скалярная передаточная функция от i - того входа y_i к j - тому выходу x_j

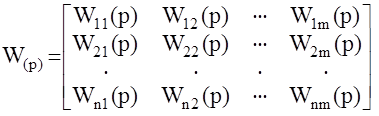Матрица (рЕ-А) называется

характеристической матрицей для матрицы состояния А. Ее определитель det(Ep-A) называется характеристическим определителем или

характеристическим полиномом системы. Он определяет собой степенной полином переменной Лапласа р порядка n.

Так как обратную характеристическую матрицу можно записать так: 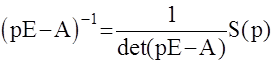S(p)- союзная матрица для (рЕ-А).

Это означает, что матричная передаточная функция МАС равна:

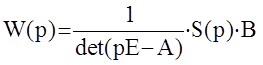
Отсюда следует важнейший вывод, что все скалярные передаточные функции многомерной АС имеют один и тот же характеристический полином. Следовательно, анализ МАС в основном сводится к анализу корней этого полинома.