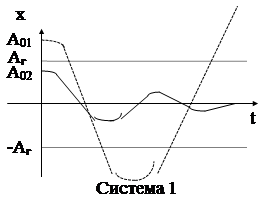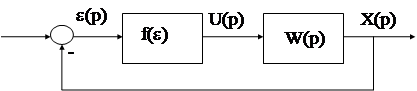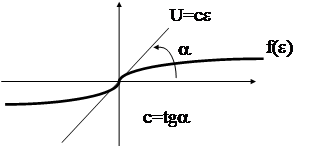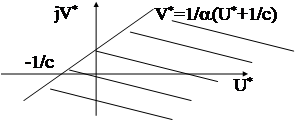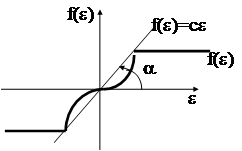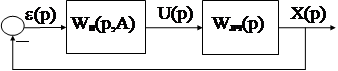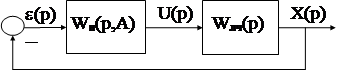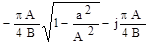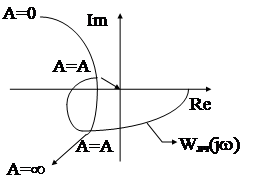Устойчивость нелинейных АС
7.1Общие положения
|
В отличие от линейных систем понятие устойчивости для НАС имеет ряд особенностей. Это связано с тем, что устойчивость НАС определяется не только структурой и параметрами самой системы, но и параметрами входного сигнала ( в частности его амплитудой). Поясним это положение графически.
При начальных отклонениях А01 > АГ (граничное значение) собственное движение первой системы расходящееся (неустойчивое), а при А02 < АГ - сходящееся (устойчивое). Для второй системы наоборот. Причем для обеих систем характерен некоторый равновесный режим ( при А=АГ ), характеризующийся незатухающими колебаниями. Говорят, что система 1 неустойчива в большом (А0>АГ), но устойчива в малом (А0< АГ). Система 2 наоборот устойчива в большом, но неустойчива в малом. Причем между этими областями устойчивости и неустойчивости существует специфический режим, называемый автоколебательным, который в свою очередь может быть устойчивым (система 2) или неустойчивым (система 1).
Кроме того, существуют нелинейные системы, которые устойчивы при любых видах входных сигналов и типах нелинейностей или наоборот неустойчивы. Такие системы называются абсолютно устойчивыми либо абсолютно неустойчивыми.
Таким образом, в отличие от линейных систем устойчивость для нелинейных АС включает в себя ряд новых понятий : устойчивость в большом или малом, устойчивость автоколебаний, абсолютная устойчивость и неустойчивость. Поясним это графически.
|
Если сравнивать с линейными системами, у которых между областями устойчивости и неустойчивости существует четкая граница, соответствующая границе устойчивости, то для НАС эта граница превращается в некоторую область, в которой возможна устойчивость в большом либо в малом. Кроме того в этой области возможно наличие автоколебаний, которые в свою очередь могут быть устойчивыми либо неустойчивыми.
Итак, анализ устойчивости нелинейных АС можно свести к следующей методике:
-оценка абсолютной устойчивости НАС ( вне зависимости от начальных условий и вида нелинейностей);
- оценка существования и устойчивости автоколебаний в системе ( уже с учетом начальных условий и видов нелинейностей);
- если в системе существуют автоколебания, то по ним однозначно определяются области устойчивости в малом либо в большом.
Рассмотрим существующие методы реализации этой методики.
7.2.Частотный критерий абсолютной устойчивости В.М.Попова.
|
|
и подчиняющуюся следующим условиям :
- линейная часть системы устойчива;
- функция передачи НЭ безынерционна (нет элементов запаздывания) и однозначна (нет гистерезиса);
|
- существует некоторый коэффициент С такой, что нелинейная характеристика ограничена прямой U=ce, то есть ½f (e)½£ C½e½. Другими словами, f(e) лежит всегда под прямой U=ce.При этих условиях румынским ученым В.М.Поповым был сформулирован критерий, определяющий достаточные условия абсолютной устойчивости НАС.
Теорема: Для того чтобы нелинейная система была абсолютно устой-
чивой, достаточно, чтобы существовало такое действитель-
ное число a, при котором действительная часть функции
П(jw) была положительной.
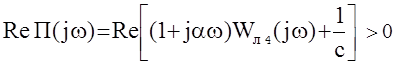 .
.
Рассмотрим геометрическую интерпретацию данного критерия. Пусть АФЧХ линейной части системы Wлч(jw)=U(w)+jV(w), тогда условие Попова запишется так:
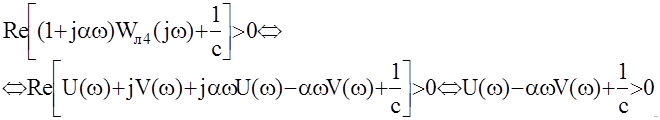 Примем обозначения
Примем обозначения 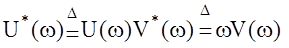 ,
,
где 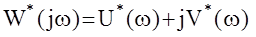 - видоизмененная линейная часть
- видоизмененная линейная часть
системы.
Тогда: 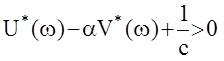 или
или 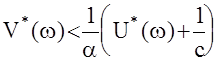 .
.
|
Геометрическое место точек на комплексной плоскости, удовлетворяющее данному неравенству, можно изобразить так.
То есть для абсолютной устойчивости НАС достаточно, чтобы на комплексной плоскости через точку с координатами (-1/с, j0) можно было провести прямую так, чтобы АФЧХ видоизмененной линейной части системы 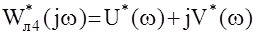 располагалась бы целиком справа от этой прямой.
располагалась бы целиком справа от этой прямой.
|
К сожалению этот критерий определяет только достаточные условия абсолютной устойчивости: то есть если он выполняется, то система абсолютно устойчива. Но если не выполняется, это не означает, что система абсолютно неустойчива - требуется применение других методов, в частности методов Ляпунова.
Таким образом, алгоритм использования критерия В.М.Попова для оценки абсолютной устойчивости НАС сводится к следующему:
- по виду нелинейной характеристики f(e) определяется коэффициент с
|
такой что 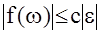 . Обычно на практике выбирается наименьшее значение с, когда
. Обычно на практике выбирается наименьшее значение с, когда 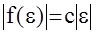 ;
;
- определение вещественной и мнимой частотных характеристик преобразованной линейной части системы
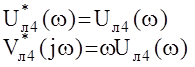
и построение АФЧХ 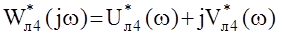 ;
;
- оценка существования прямой 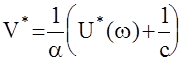 такой, что
такой, что
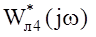 лежит целиком справа от этой прямой..
лежит целиком справа от этой прямой..
7.3.Оценка устойчивости нелинейных АС прямым методом
А.М.Ляпунова.
Наиболее общим побходом к оценке устойчивости АС является использование методов Ляпунова. Первый метод, основанный на анализе решений дифференциальных уравнений, очень трудоемок и применим в основном для оценки устойчивости в малом. Второй или прямой метод Ляпунова позволяет оценить устойчивость АС, не производя решение самих уравнений.
Пусть НАС описывается нелинейным дифференциальным оператором вида:
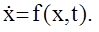
Введем в рассмотрение некоторую функцию V(x,t), которая положительна при любых значениях x,t за исключением начала координат (x=0, t=0), где V=0.Такие функции получили название функций Ляпунова. Определим полную производную V по времени на уравнениях движения рассматриваемой системы:
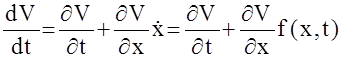 Сформулируем теперь собственно теорему Ляпунова.
Сформулируем теперь собственно теорему Ляпунова.
| Теорема: (2-й метод Ляпунова) |
Для того, чтобы НАС была асимптотически устойчивой достаточно, чтобы для нее можно было найти такую положительно определенную функцию Ляпунова, производная от которой на уравнениях движения системы отрицательна.
Пример: Оператор НАС имеет вид:
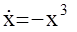
Выберем функцию V(x,t)=x2, которая положительна при любых х и равна нулю только при х=0.Производная:
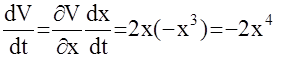 отрицательна при любых х, следовательно данная АС асимптотически устойчива.
отрицательна при любых х, следовательно данная АС асимптотически устойчива.
Отметим, что прямой метод Ляпунова дает оценку достаточных условий асимптотической устойчивости НАС, более широкого понятия чем абсолютная устойчивость. Однако практическое применение метода затруднено тем, что не существует общего подхода к определению функций Ляпунова. Это сужает область его применения.
7.4.Анализ автоколебаний в НАС.
Как уже отмечалось, если не удалось выяснить вопрос об абсолютной устойчивости НАС, дальнейшее исследование сводится к выявлению автоколебательных режимов в системе.
Автоколебания - это незатухающие периодические колебания с постоянной частотой w и постоянной амплитудой А.
Анализ автоколебательных режимов в НАС обычно проводится приближенными методами, основанными на гармонической линеаризации нелинейных элементов, входящих в систему. Напомним, что в результате гармонической линеаризации нелинейный элемент с функцией передачи f(e) заменяется эквивалентным линейным с передаточной функцией WH(p,A). Причём режим автоколебаний предполагает отсутствие входного сигнала U(p)=0.
|
Анализ автоколебаний в НАС сводится к выяснению вопросов их существования и единственности. Рассмотрим решение этих вопросов двумя методами: аналитическим методом гармонического баланса и графоаналитическим методом Гольдфарба.
7.5.Метод гармонического баланса.
Допустим, что в гармонически линеаризованной НАС существует режим автоколебаний
|
Очевидно, что для такой системы эти автоколебания возможны при соблюдении следующего условия Х(р)= -e(р), то есть входной сигнал находится в противофазе с выходным и совпадает с ним по амплитуде. Переходя к передаточным функциям
WH(p,A) Wлч(р) e(р) = - e(р) или WH(p,A) Wлч(р) = - 1
Перейдем в этом выражении к частотным характеристикам (p=jw) и учтем, что для гармонически линеаризованных НАС WH(jw,A)=WH(A).Тогда:
WH(A) Wлч(jw) = - 1.
Данное уравнение называется уравнением гармонического баланса в комплексной форме.
Существование решения этого уравнения означает существование автоколебаний в системе, а само решение есть их амплитуда А и частота w. Но с другой стороны решение такого комплексного уравнения достаточно трудная задача, поэтому на практике его представляют в виде системы двух уравнений: для амплитудночастотных и фазочастотных характеристик: 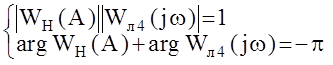 и по отдельности решают каждое.
и по отдельности решают каждое.
Первое уравнение получило название баланс амплитуд, второе - баланс фаз, а их решение составляет суть метода гармонического баланса. Основной недостаток данного метода в том, что он не позволяет дать ответ на вопрос об устойчивости полученных решений (автоколебаний).
7.6.Графоаналитический метод Гольдфарба.
Если в НАС существуют автоколебания, то выполняется условие гармонического баланса WH(A) Wлч(jw) = -1 или Wлч(jw)=1/WH(A)=
= -ЕН(А), здесь ЕН(А) - обратная частотная характеристика существенно НЭ.Приведем наиболее распространенные обратные частотные характеристики:
| Тип НЭ | Wн(А) | -Ен(А) | ||||||||||||||||||||||||
| 4B pA | |||||||||||||||||||||||||
 
   
|
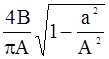
| |||||||||||||||||||||||||
|
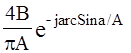
|
|
 Последнее уравнение решается графически: строятся графики АФЧХ линейной части Wлч(jw) и -ЕН(А).Если есть точки пересечения - это значит, что в НАС существуют автоколебания.Ответ же на вопрос о том будут ли они устойчивыми, дает специальное правило, установленное Л.С.Гольдфарбом (1947г.).
Последнее уравнение решается графически: строятся графики АФЧХ линейной части Wлч(jw) и -ЕН(А).Если есть точки пересечения - это значит, что в НАС существуют автоколебания.Ответ же на вопрос о том будут ли они устойчивыми, дает специальное правило, установленное Л.С.Гольдфарбом (1947г.).
Автоколебания будут устойчивыми, если при увеличении амплитуды А годограф обратной частотной характеристики -ЕН(А) при пересечении с АФЧХ линейной части выходит из области, охватываемой Wлч(jw).
На представленном рисунке автоколебания амплитуды А1 неустойчивы, а с амплитудой А2 устойчивы, причем А2>A1. Отметим также, что частота всех возможных автоколебаний одна и таже (относительно которой осуществляется гармоническая линеаризация). Таким образом, общая методика анализа автоколебаний в НАС методом Гольдфарба сводится к следующему:
- построение на комплексной плоскости годографов -ЕН(А), Wлч(jw);
- оценка существования (наличие точек пересечения) и устойчивости (правило Гольдфарба) автоколебательных режимов;
- графоаналитическое определение амплитуды А и частоты w устойчивых автоколебаний в НАС.
Отметим также интересную особенность. Для рассмотренных видов нелинейностей, обратные частотные характеристики которых располагаются целиком в левой комплексной полуплоскости, автоколебания возможны лишь в случае если линейная часть системы имеет порядок n³ 2.
| <== предыдущая лекция | | | следующая лекция ==> |
| Общие понятия о нелинейных системах | | | Математические модели многомерных автоматических систем |
Дата добавления: 2015-12-16; просмотров: 1662;