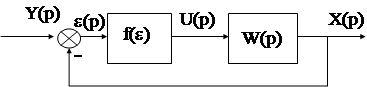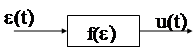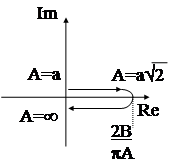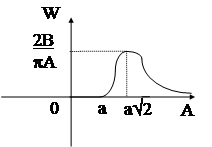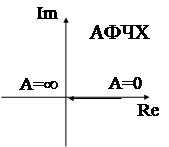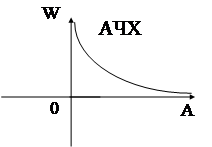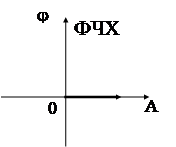Общие понятия о нелинейных системах
6.1Понятие о нелинейных АС и методах их исследования
Нелинейными называются АС, к операторам которых не применим принцип суперпозиции. То есть реакция системы на сумму входных сигналов не может быть представлена в виде суммы соответствующих реакций. Кроме того, пропорциональное увеличение входного сигнала приводит к изменению не только амплитуды, но и формы выходного сигнала. В силу этого методы, разработанные для линейных систем, становятся непригодными при анализе нелинейных. Возникает проблема разработки специального математического аппарата для анализа и синтеза нелинейных АС (НАС).
|
Несмотря на сложность исследования и конструирования таких систем, они находят достаточно широкое распространение на практике. Это связано с тем, что в ряде задач они являются более предпочтительными перед линейными по своему быстродействию, точности, а в отдельных случаях и простоте. К примеру, выходные характеристики рулевого привода современных самолетов имеют следующий вид.
Введение такой нелинейной характеристики с насыщением позволяет ограничивать максимальные отклонения органов управления самолета и тем самым предотвращать его выход на критические режимы. А реализация такой зависимости предельно проста: обычные упоры.
В общем случае любая АС может считаться нелинейной, а процессы в ней описываются нелинейными уравнениями вида:
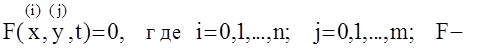 некоторый нелинейный оператор.
некоторый нелинейный оператор.
В отдельных случаях данное уравнение можно линеаризовать (например,, разложением в ряд Тэйлора относительно опорного движения), то есть от исходной нелинейной системы перейти к эквивалентной линеаризованной и исследовать её достаточно хорошо разработанными методами для линейных систем. Однако часто бывает, что такая линеаризация невозможна:
а) когда не существует опорного движения (например, штопор самолёта);
б) когда отклонения выходных и входных сигналов от опорного движения значительны и отбрасывание нелинейных членов ряда Тэйлора при линеаризации приводит к недопустимым погрешностям;
в) АС содержит элементы, характеристики которых претерпевают разрывы, то есть соответствующие производные либо неограничен, либо не существуют.
В дальнейшем под общим термином «нелинейные АС» будем понимать именно такие существенно нелинейные системы. Для их исследования применяются специальные методы, которые будут рассмотрены ниже.
6.2Существенно нелинейные элементы
Любая НАС представляет собой соединение одного или нескольких нелинейных элементов (НЭ) и линейной части.
|
Здесь f(e)- функция передачи существенно нелинейного элемента;
Wлч(р)- передаточная функция линейной части системы.
Существенно нелинейным называется элемент НАС, функция передачи которого в области изменения входного сигнала или неоднозначна или не имеет ограниченных по величине производных.
В свою очередь существенно нелинейные элементы разделяются на непрерывные, характеристики которых не претерпевают разрывы, и релейные. Некоторые типовые нелинейности приведены в таблице.
| № | f(e) | Наименование | ||||||||||||
   
 

| НЭ с ограничением (с насыщением) | |||||||||||||
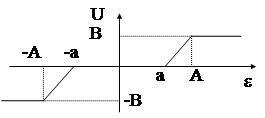
| НЭ с зоной нечувствительности и ограничением | |||||||||||||
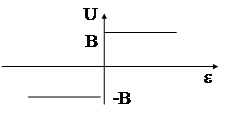
| Идеальное двухпозиционное реле | |||||||||||||
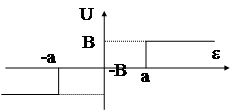
| Трехпозиционное реле (реле с зоной нечувствительности) | |||||||||||||
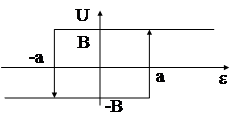
| Двухпозиционное реле с гистерезисом |
Наиболее общим методом исследования таких существенно нелинейных систем является решение систем нелинейных дифференциальных уравнений, описывающих динамику НАС, на современных ЭВМ. Однако часто это затруднительно, требует довольно громоздких и длительных предварительных расчетов. Поэтому в практике исследования НАС широкое распространение получили методы анализа, основанные на предварительной линеаризации существенно нелинейных элементов. В качестве таких методов линеаризации чаще всего используются гармоническая и статистическая линеаризация нелинейностей.
6.3.Гармоническая линеаризация нелинейностей
Пусть на вход существенно нелинейного элемента с функцией передачи f(e) действует некоторый гармонический сигнал e(t)=ASinwt.
|
Выходной сигнал u(t) в общем случае представляет собой некоторую нелинейную функцию, которая может быть разложена в ряд Фурье:
u(t)=u0+A1Sinwt+B1Coswt+A2Sin2wt+B2Cos2wt+...,
где w- частота входного сигнала (первая гармоника);
Аi, Bi - коэффициенты ряда Фурье;
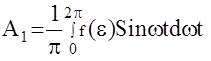 ,
, 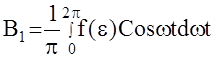 ,
, 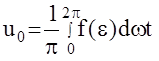 ,
,
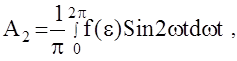
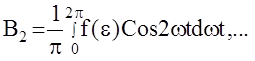
Для большинства авиационных АС можно принять следующие допущения:
1.Линейная часть системы, на которую поступает сигнал u(t), является фильтром низких частот, пропускающим только первую гармонику u(t) (частоты w) и ослабляющим все остальные (2w,3w,4w...)
2.Характеристика НЭ является функцией нечетной, а это значит, что 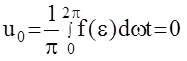 (интеграл от нечетной функции в симметричных пределах или на периоде равен 0).
(интеграл от нечетной функции в симметричных пределах или на периоде равен 0).
Эти допущения называются основными допущениями метода гармонической линеаризации. Они позволяют применять для анализа НАС частотные методы, разработанные для линейных систем.
В силу сделанных допущений имеем:
u(t)»u1(t)=A1Sinwt+B1Coswt , где 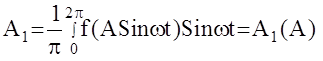 ,
,
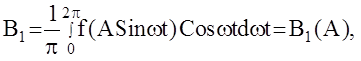 то есть коэффициенты А1 и В1 выходного сигнала НЭ зависят от вида нелинейности f(e) и амплитуды выходного сигнала А и не зависят от его частоты w. Воспользовавшись соотношениями :
то есть коэффициенты А1 и В1 выходного сигнала НЭ зависят от вида нелинейности f(e) и амплитуды выходного сигнала А и не зависят от его частоты w. Воспользовавшись соотношениями :
e(t)=ASinwtÞSinwt=e(t)/A; 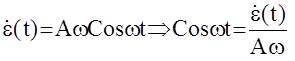
можно записать:
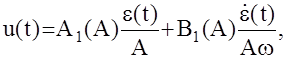
или, применив преобразования Лапласа при нулевых НУ:
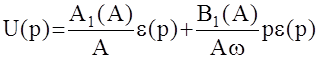 ,
,
с другой стороны:
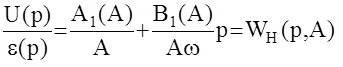
Эквивалентной передаточной функцией гармонически линеаризованного нелинейного элемента называется отношение изображения по Лапласу первого гармоники выходного сигнала к изображению входного синусоидального сигнала при нулевых начальных условиях.
6.4.Частотные характеристики гармонически линеаризованных
нелинейных систем.
АФЧХ гармонически линеаризованной системы можно получить из эквивалентной передаточной функции путем замены переменной Лапласа р на комплексную переменную jw.
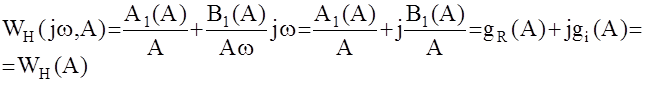
здесь gR(A)- вещественная частотная характеристика;
gi(A)- мнимая частотная характеристика.
Таким образом, АФЧХ системы не зависит от частоты входного сигнала, а является только функцией его амплитуды. Несмотря на кажущийся парадокс, это объясняется тем, что гармоническая линеаризация допустима только для одной фиксированной частоты (первой гармоники). Определим теперь частотные характеристики некоторых существенно нелинейных элементов.
6.4.1Частотные характеристики реле с зоной нечувствительности.
Пусть на вход реле с зоной нечувствительности действует синусоидальный входной сигнал e(t)=ASinwt.
Графически это можно представить так.
|
Используя эти графики, определим АФЧХ данного реле по формуле :
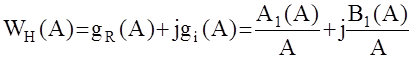 ,
,
здесь А1(А), В1(А) - коэффициенты ряда Фурье.
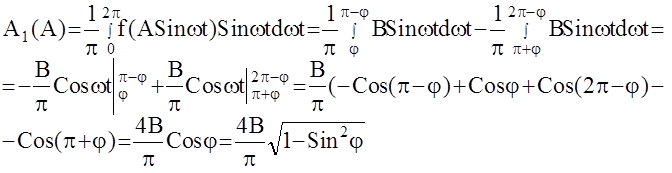
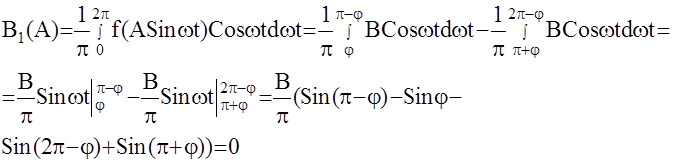 Угол j можно определить из условия:
Угол j можно определить из условия: 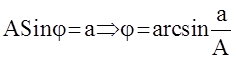 , в итоге получаем:
, в итоге получаем: 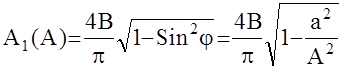 .
.
Откуда АФЧХ WH(A) определяется так:
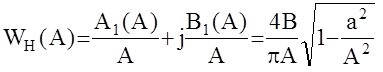 .
.
Таким образом, АФЧХ реле с зоной нечувствительности есть функция действительная (следовательно совпадает с АЧХ) и на комплексной плоскости при изменении амплитуды входного сигнала А изображающая точка перемещается по действительной оси.
|
Поскольку частотные характеристики строятся не в функции частоты, а в функции амплитуды входного сигнала А, диапазон изменения которой достаточно узок, то нет смысла вводить логарифмические частотные хакрактеристики для таких систем.
Итак, семейство частотных характеристик для гармонически линеаризованных нелинейных систем включает в себя : АФЧХ, АЧХ и ФЧХ системы.
6.4.2Частотные характеристики идеального двухпозиционного реле
Вновь графически изобразим входные и выходные сигналы такой системы:
|
Как видим, выходной сигнал, а следовательно и АФЧХ идеального двухпозиционного реле, есть частный случай трехпозиционного реле с зоной нечувствительности а = 0. Следовательно 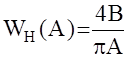 . Вновь получили, что АФЧХ такой системы есть функция действительная, следовательно, совпадает с АЧХ, а ФЧХ равна нулю.
. Вновь получили, что АФЧХ такой системы есть функция действительная, следовательно, совпадает с АЧХ, а ФЧХ равна нулю.
|
6.4.3Частотные характеристики двухпозиционного реле с гистерезисом.
Опять применим тот же графический подход:
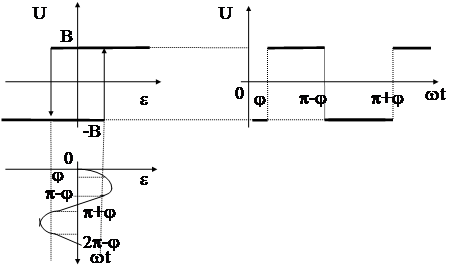
|
Как видим, выходной сигнал реле с гистерезисом, запаздывает по фазе от выходного сигнала идеального двухпозиционного реле на величину
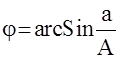 , а сам вид этого сигнала остался прежним, то есть АЧХ этих систем совпадают
, а сам вид этого сигнала остался прежним, то есть АЧХ этих систем совпадают 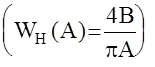
 , а фазочастотная характеристика j(А) для реле с гистерезисом имеет вид
, а фазочастотная характеристика j(А) для реле с гистерезисом имеет вид 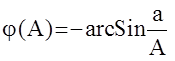 .Следовательно, АФЧХ имеет вид :
.Следовательно, АФЧХ имеет вид : 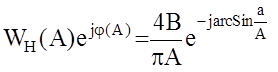 ;
;
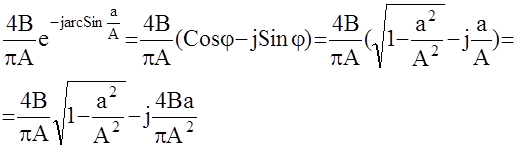
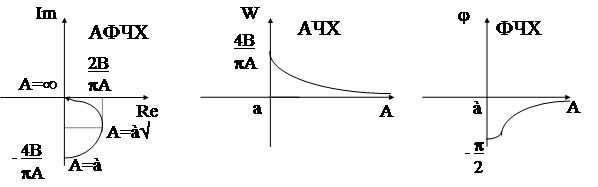 |
Графически это изображается так:
| <== предыдущая лекция | | | следующая лекция ==> |
| Синтез линейных АС классическими методами. | | | Устойчивость нелинейных АС |
Дата добавления: 2015-12-16; просмотров: 3640;