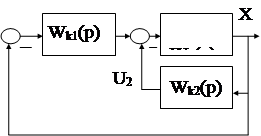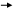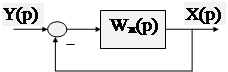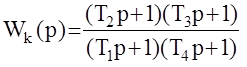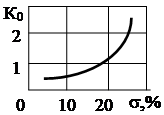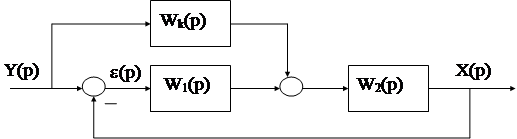Синтез линейных АС классическими методами.

5.1.Общая и частная задача синтеза АС.

На основе проведенного анализа делается вывод соответствует ли данная АС некоторым выбранным критериям. В случае несоответствия возникает проблема: каким путем изменить систему так, чтобы она обладала желаемым качеством. Решение этой задачи и составляет суть синтеза АС.

Синтез АС- это определение структуры, состава элементов и значений параметров АС, при которых она удовлетворяет предъявляемым к ней требованиям.

Приведенное определение характеризует общую задачу синтеза АС в классической постановке, которая решается обычно в следующем порядке:

1.Выбираются основные функционально необходимые элементы АС с учетом обеспечения энергетических, эксплуатационных и других требований, предъявляемых к системе.

2. Составляется функциональная схема АС.

3. Определяются дифференциальные уравнения и передаточные функции элементов АС, численные значения их коэффициентов.

4. На основании известных методов производится оценка устойчивости и качества АС. Если требования к устойчивости и качеству не выполняются, то стараются добиться улучшения качества процесса управления за счет изменения основных элементов системы.

5. Если не возможно добиться удовлетворения всех требований, предъявляемых к АС выбором только основных элементов, то в систему вводятся специальные дополнительные устройства, называемые корректирующими ( КУ).

Задача определения типа и параметров корректирующего устройства называется частной задачей классического синтеза АС.

5.2.Корректирующие устройства и их влияние на качество переходных процессов.

При решении частной задачи синтеза, АС представляется в виде неизменяемой части с ПФ W₀(p) и корректирующих устройств с передаточными функциями W_ki(p).

W₂(p) -ПФ параллельного КУ, включа-

емого в цепь местной обратной связи.

Задача КУ - это формирование сигнала U(p) (U₁(p),U₂(p)), подаваемого на входы исполнительных устройств объекта управления, то есть, иначе говоря, формирование закона управления АС.

Законом управления АС называется зависимость сигнала, подава-

емого на вход исполнительного устройства, от входных и выход-

ных сигналов системы : u(t) =f[x(t),y(t),e(t)].

Как видим, законы управления последовательных и параллельных КУ отличаются своими входными сигналами: так для параллельных КУ входными являются достаточно мощные сигналы оконечных каскадов АС, поэтому нет необходимости в их предварительном усилении, что в свою очередь снижает уровень высокочастотных помех на входах исполнительных устройств. Последовательным КУ присущи эти недостатки, но в отличии от параллельных они гораздо проще реализуются на практике.Рассмотрим наиболее распространенные законы управления последовательных и параллельных КУ.

5.3Введение в закон управления производной от регулируемой

величины.

Простейшим законом управления последовательного КУ является закон вида : u(t)=k₁e(t)Û U(p)=k₁e(p).

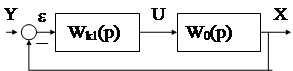
Передаточная функция

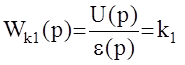-соответствует усилительному звену.

При увеличении коэффициента усиления разомкнутой системы k, как известно, уменьшается установившаяся ошибка АС

.

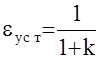Однако возможность улучшения качества за счет увеличения только коэффициента усиления в значительной мере ограничена требованиями к устойчивости. Поэтому, несмотря на свою исключительную простоту, такой закон управления применяется очень редко.

Рассмотрим закон управления с производной от регулируемой величины: u(t)=k₁e(t)+k₂e^’(t) Û U(p)=k₁e(p)+k₂pe(p)

W(p)=(k₁+k₂p)=k(Tp+1), k=k₁; T=k₂/k₁.

Таким образом, введение в закон управления производной от регулируемой величины, соответствует включению идеального форсирующего звена в разомкнутый контур системы.

5.4.Введение в закон управления интеграла от регулируемой

величины.

Закон управления в этом случае имеет вид:

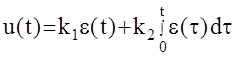
Передаточная функция КУ:

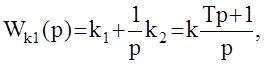k=k₂

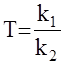
Таким образом, введение такого корректирующего устройства приводит к повышению порядка астатизма системы за счет введения свободного интегрирующего звена (причем без ухудшения структурной устойчивости за счет форсирующего звена).

С другой стороны фазочастотная характеристика такого КУ: j_k(w)=-p/2+arctgwT<0 во всем диапазоне частот меньше нуля, что приводит к снижению запаса устойчивости системы Dj_{з ск}=Dj_{з 0}+j_k(w_c), а следовательно к ухудшению качества в переходных режимах.

Такой закон управления получил широкое распространение в системах посадки, где особенно важна точность управления.

5.5.Жесткие и изодромные обратные связи.

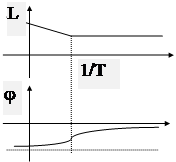
В зависимости от вида передаточных функций параллельных КУ различают жесткие и гибкие обратные связи.

Здесь W₁(p) - передаточная функция некорректируемой части системы;

W₂(p)-передаточная функция корректируемой части;

W_k(p)-ПФ параллельного кор­ректирующего устройства.

Жесткой обратной связью (ЖОС), называется параллельное КУ с ПФ: W_k(p)=k₁, или законом управления u₂(t)=k₁x(t).

Гибкой обратной связью (ГОС), называется параллельное КУ с ПФ, содержащей р в числителе.

Рассмотрим действие ЖОС и ГОС на характеристики системы, у которой .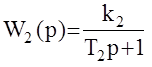

При W_k(p)=k₁ имеем: 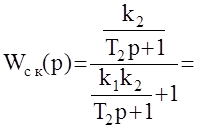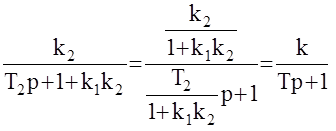.k<k₂ , T<T₂

Как видим введение ЖОС приводит к уменьшению постоянной времени Т<T₂ скорректированной части, а следовательно к повышению быстродействия, но с другой стороны уменьшается общий коэффициент усиления разомкнутой системы k<k₂, что ухудшает точность в установившемся режиме 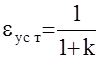. Можно сказать, что ЖОС действует как в переходных так и в установившихся режимах, что не всегда желательно. ГОС обычно действует только в переходных режимах.

Например:W_k(p)=k₁p , тогда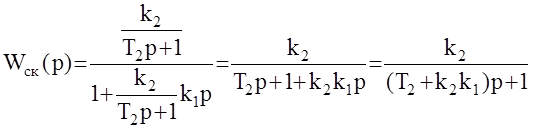

Как видим, изменилась только постоянная времени Т, а коэффициент усиления корректируемой части остался неизменным. В итоге удалось изменить инерционные свойства системы, не ухудшая ее точность. На практике, в силу физической нереализуемости КУ с передаточными функциями W_к(р)=kp, применяют так называемые изодромные обратные связи с ПФ 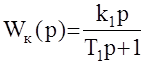, соответствующей реальному дифференцирующему звену (Т₁<< Т₂).

5.6.Синтез последовательного корректирующего устройства с помощью ЛАЧХ.

Наиболее общим подходом к синтезу корректирующих устройств является подход с использованием логарифмических частотных характеристик. Так как обычно рассматриваются минимально-фазовые системы (все нули и полюса которых лежат в левой полуплоскости), то при синтезе достаточно рассматривать только логарифмические амплитудно-частотные характеристики (так как ЛАЧХ и ЛФЧХ в этом случае взаимно-однозначно связаны).

Исходными данными при синтезе любой АС являются: требования к качеству, задаваемые известными критериями: t_p, s, t_ср, e_уст, ... Допустим, что указанным требованиям удовлетворяет система с ПФ W_ж(р), которую можно представить как исходную систему с введенным последовательным КУ.

Здесь W_ж(р)- ПФ системы с желаемыми характеристиками качества; W₀(p)- ПФ исходной системы; W_k(p)- ПФ последовательного КУ.

В силу предполагаемой эквивалентности этих систем:

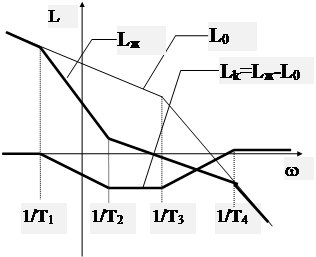
W_ж(р)=W_k(p) W₀(p), или переходя к ЛАЧХ L_k(w)=L_ж(w)-L₀(w).

Данная формула является основной расчетной для определения параметров последовательного КУ, доставляющего исходной системе желаемые характеристики качества.

Рассмотрим методику синтеза последовательного КУ на следующем примере: , .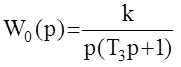

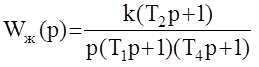1. Используя известную связь между видом ЛАЧХ и заданными критериями качества, строится ЛАЧХ желаемой системы.

2. На этом же графике строится ЛАЧХ исходной системы L₀(w).

3. Определяется ЛАЧХ корректирующего устройства путем графического вычитания L_k(w)=L_ж(w)-L₀(w).

4. По виду L_k(w) определяется передаточная функция корректирующего устройства W_k(p) .

5. Проводится оценка физической реализуемости КУ по виду W_k(p).

6. Если КУ нереализуемо или очень сложное, проводят изменение L_ж(w) так, чтобы удовлетворить требования и к качеству и к реализуемости.

Поскольку такая методика синтеза почти не требует аналитических расчетов, она нашла достаточно широкое распространение на практике.

Обобщая всё вышесказанное по последовательным корректирующим устройствам, можно сделать следующие основные выводы:

+ простота синтеза и реализации таких устройств (законов управления);

- высокие требования в отношении стабильности параметров корректируемой системы;

- наличие дифференцирующих и форсирующих звеньев приводит к увеличению уровня высокочастотных помех.

5.7.Синтез параллельных корректирующих устройств с помощью ЛАЧХ

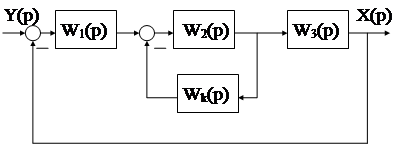
Синтез параллельного КУ с помощью ЛАЧХ имеет ряд особенностей по сравнению с синтезом последовательного КУ. Выведем основные расчётные соотношения для определения ЛАЧХ параллельного КУ для представленной структурной схемы. Пусть данная скорректированная система обладает желаемыми характеристиками качества. ПФ разомкнутой системы имеет вид:

W_ж(р)=W₁(p)W₂(p)W₃(p)/(1+W₂(p)W_k(p))=W₁₃W₂/(1+W₂W_k), W₁₃=W₁W₃

АФЧХ такой системы равна: W_ж(jw) = W₁₃(jw)W₂(jw)/(1+W₂(jw)W_k(jw)).

При синтезе параллельного КУ используется тот же подход, что и при построении асимптотических логарифмических частотных характеристик. Весь диапазон частот разбивается на два поддиапазона, удовлетворяющих условиям:

первый-½W₂(jw)W_k(jw)½< < 1, второй-½W₂(jw)W_k(jw)½> > 1.

Эти условия для логарифмических характеристик можно записать так:

L₂(w) + L_k(w) < 0 , L₂(w) + L_k(w) > 0.

В первом диапазоне АФЧХ системы имеет вид (пренебрегаем W₂(jw)W_k(jw) по сравнению с 1) :

W_ж(jw)=W₁₃(jw)W₂(jw)=W_н(jw)- АФЧХ нескорректированной системы.

Итак, можно сказать, что первый диапазон характеризуется условием L_ж(w)=L_н(w) и в этом диапазоне L_k(w) следует выбирать из соотношения L_k(w)< -L₂(w).

Во втором диапазоне АФЧХ системы имеет вид :

W_ж(jw)=W₁₃(jw)W₂(jw)/W₂(jw)W_k(jw)=W₁₃(jw)/W_k(Jw)

(пренебрегаем 1 по сравнению с W₂(jw)W_k(jw)) или, переходя к ЛАЧХ:

L_ж(w)=L₁₃(w) - L_k(w) или L_ж(w) < L_н(w), и в этом диапазоне L_k(w) следует выбирать из соотношения : L_k(w)=L₁₃(w)-L_ж(w).

Таким образом, получены правила разбиения всего диапазона частот на поддиапазоны и правила выбора L_k(w) в этих поддиапазонах. Сформулируем теперь общую методику синтеза параллельного КУ по логарифмическим частотным характеристикам.

1.Строится ЛАЧХ нескорректированной системы L_н(w) и ЛАЧХ желаемой системы L_ж(w). Причем во всем диапазоне частот должно выполняться условие L_ж(w) £ L_н(w)

2.Строится ЛАЧХ некорректируемой части системы L₁₃(w) и обратная ЛАЧХ корректируемой части -L₂(w).

3.Выделяются поддиапазоны где L_ж=L_н(w) , L_ж< L_н(w).

4.Во втором диапазоне ЛАЧХ корректирующего устройства выбирается из условия L_k(w)=L₁₃(w)-L_ж(w). В первом диапазоне должно выполняться соотношение L_k(w)< -L₂(w).

5.По виду L_k(w) определяется ПФ корректирующего устройства W_k(p) и проверяются условия его физической реализуемости.

5.8.Методика построения желаемой ЛАЧХ.

Построение L_ж(w) является ключевым этапом синтеза КУ.Здесь необходимо учитывать два противоречивых условия:

n синтезированная система должна удовлетворять заданным требованиям;

n коректирующее устройство (или закон управления), получаемое в результате синтеза, должно быть простым в реализации.

Желаемую ЛАЧХ можно условно разделить на три части : низкочастотную, среднечастотную, высокочастотную.

Низкочастотная часть определяет статические свойства системы и задается она обычно коэффициентами усиления k (или e_уст= 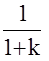) и требуемым порядком астатизма n.

Среднечастотная часть является наиболее важной. Она определяет устойчивость, запас устойчивости и качество переходных процессов, оцениваемое обычно прямыми показателями качества. Основные параметры среднечастотной асимптоты - это ее наклон, протяженность и частота среза w_с. Чем больше наклон среднечастотной асимптоты, тем труднее обеспечить хорошие динамические свойства системы. Поэтому наиболее целесообразным является наклон - 20 дБ/дк. Частота среза определяет быстродействие системы. Чем больше w_с тем меньше время регулирования t_p, тем выше быстродействие.

Высокочастотная часть желаемой ЛАЧХ незначительно влияет на качество системы. Поэтому обычно высокочастотную ЛАЧХ проводят так, чтобы она совпадала с ЛАЧХ нескорректированной системы для упрощения ПФ корректирующего устройства.

Наиболее общий вид желаемой ЛАЧХ следующий. Она характеризуется следующими параметрами: n-порядок астатизма системы.;

s-наклон участка сопряжения среднечастотной и низкочастотной асимптот;

w_с-частота среза системы;

w₂-ближайшая слева к частоте среза частота сопряжения ;

w₃-ближайшая справа к частоте среза час­тота сопряжения;

w₁-первая частота сопряжения.

В настоящее время разработаны различные точные методы построения желаемой ЛАЧХ (Солодовникова, Санковского, Сигалова,...) по заданным критериям качества. Однако они достаточно сложны, поэтому на практике более часто пользуются упрощенными методами построения желаемой ЛАЧХ с последующим ее уточнением.

Рассмотрим один из таких методов.

1.Исходя из требований к точности АС в установившемся режиме определяют величины порядка астатизма n и коэффициента усиления K. Для найденных значений n и К строится низкочастотная асимптота.

2.Выбирают частоту среза по формуле ,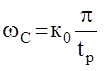

где к₀ определяется из графика.

3.Определяют частоты w₂, w₃, ограничивающие среднечастотную асимптоту соответственно слева и справа. Хорошие характеристики качества (s < 16%, Dj_з> p/6) обеспечиваются в случае: w₃=(2¸4)w_С, w₂£ 0,1 w₃.

4.Сопрягают среднечастотную и низкочастотную асимптоты прямой с наклоном - 20S. При этом следует помнить, что чем больше S тем меньше запас устойчивости.

5.Высокочастотную часть строят совпадающей с ЛАЧХ нескорректированной системы, для упрощения получаемого КУ.

6.Во всем диапазоне частот должно выполняться условие L_ж(w)£ L_н(w) иначе неодходимо введение в систему дополнительных активных элементов (усилительных устройств).

5.9.Метод корневого годографа

Метод исследования АС, основанный на построении траекторий корней её характеристического полинома, называется методом корневого годографа. Он был предложен американским учёным Эвансом в 1948 г. и впервые был использован при построении системы управления самолёта В-52.

В качестве свободного параметра, в функции которого строятся траектории корней, обычно рассматривается коэффициент усиления разомкнутой системы. Полный портрет траекторий этих корней и называется корневым годографом.

Рассмотрим такую методику синтеза АС на примере системы второго порядка с передаточной функцией:

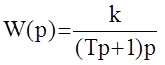. Здесь Т - известная постоянная времени; k - коэффициент усиления, изменяющийся в диапазоне от 0 до ¥.

Корни характеристического полинома замкнутой АС:

А(р) = Тр­² + р + k

равны: .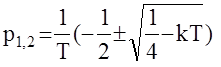

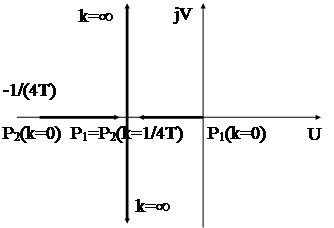
Изобразим соответствующий корневой годограф при изменении k от 0 до ¥. При увеличении k от 0 до 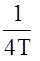корни р_1,2 являются вещественными. В точке k=1/4Т , р₁ = р₂ =-1/2Т. Далее корни становятся комплексно сопряжёнными. Имея корневой годограф системы (зная корни характеристического полинома), всегда можно оценить прямые показатели качества t_p и s и, наоборот, по этим показателям можно определить желаемый коэффициент усиления разомкнутой системы k. Если оказывается, что даже при оптимальном значении коэффициента k система не удовлетворяет предъявляемым к ней требованиям, то следует изменить параметры системы (например Т) или её структуру.

5.10.Обеспечение инвариантности в автоматических системах

Точность АС определяется ошибкой отработки задающего воздействия. Как известно, повышение точности можно добиться увеличением порядка её астатизма, то есть введением свободных интегрирующих звеньев в разомкнутый контур системы. Но это в свою очередь ведёт к такому нежелательному явлению, как снижение запаса и даже потеря устойчивости. Рассмотрим другой возможный способ повышения точности, основанный на использовании принципа комбинированного управления. Структурная схема такой АС имеет cледующий вид:

.

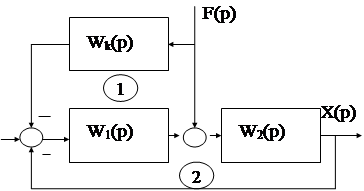
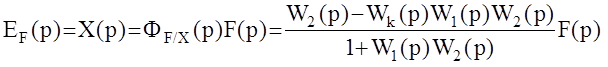Очевидно, что условие равенства нулю ошибки E_F(p) можно записать так:

W₂(p)-W_k(p)W₁(p)W₂(p)=0 ó 1-W_k(p)W₁(p) = 0.

Данное условие получило название условия абсолютной инвариантности рассматриваемой АС по отношению к возмущению F(p).

Отметим, что корректирующее устройство, получающееся по формуле: W_k(p) = 1/W₁(p), получается в большинстве случаев физически нереализуемым, однако можно добиться его практической реализации в определённом диапазоне частот и для определённых W₁(p).

Отметим также, что комбинированное управление можно применить для повышения точности следящих систем, путём обеспечения условия абсолютной инвариантности для ошибки e(р).

.

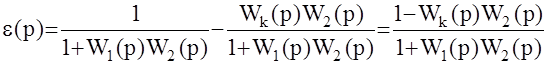Условие абсолютной инвариантности в этом случае имеет вид:

1-W₂(p)W_k(p) = 0 ó W_k(p) = 1/W₂(p).

Как видим, вновь получается физически нереализуемое корректирующее устройство, но опять же при определённых условиях практическая реализация его возможна.