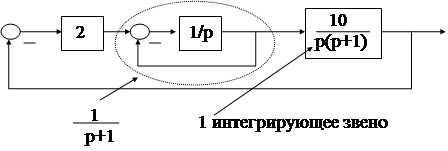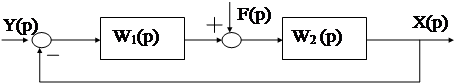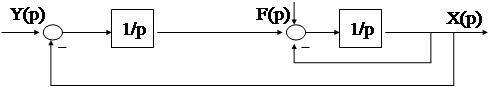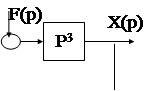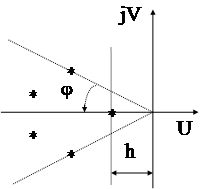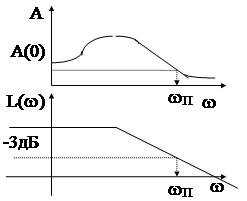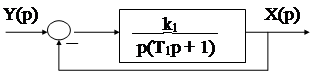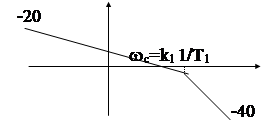Качество линейных автоматических систем
4.1Основные показатели качества АС
Устойчивость, как это было показано ранее, определяет работоспособность АС, то есть способность выполнять заданные функции. И, если система неустойчива, то вопросы дальнейшего исследования АС просто не возникают. Если же система устойчива, то очень важными становятся вопросы о том насколько хорошо, насколько качественно выполняет АС свои функции. Это свойство системы оценивается также конкретными специальными показателями, называемыми показателями качества АС.Таким образом, процесс анализа линейных АС можно представить в следующем виде.

|
Отметим, что статические режимы АС - это обычно состояние покоя или невозмущённого движения, характеризуемые некоторыми статическими (неизменными) характеристиками, например: сухой вес самолёта, порядок системы, общий коэффициент усиления и т.п. Обычно эти характеристики для любой системы определены заранее на этапе её проектирования, заданы в технических паспортах и не меняются в процессе эксплуатации. Поэтому на практике наибольший интерес представляет оценка качества АС в динамических, т.е. в переходных режимах.
4.2Оценка качества переходных процессов. Прямые показатели качества
Как известно, переходные режимы оцениваются специальным классом характеристик, называемых динамическими, к которым относятся: временные ( переходная и весовая функции ) и частотные ( амплитудные и фазовые ). По виду этих характеристик определяются специальные показатели качества, которые условно можно разделить на два больших класса : прямые и косвенные.
Прямыми называются показатели качества, вычисляемые по виду переходной функции АС.
Очевидно, когда вид переходной функции неизвестен пользуются косвенными показателями качества.

|
Рассмотрим наиболее распространенные прямые показатели качества.
tp- время регулирования (или время переходного процесса tп) - это время последнего входа в 5-ти процентный коридор относительно установившегося значения hуст ;
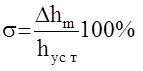 - перерегулирование - относительный максимальный заброс над установившимся значением ;
- перерегулирование - относительный максимальный заброс над установившимся значением ;
eуст = hзад - hуст - установившаяся ошибка - разность заданного и установившегося значения выходного сигнала;
tср -время срабатывания - время первого входа в 5-ти процентный коридор относительно установившегося значения.
Прямые показатели качества получили широкое распространение на практике.Это связано прежде всего с простотой их определения, наглядностью и доступностью для непосредственного восприятия инженером, летчиком, оператором. Значения их также регламентируются для различных АС и учитываются при их проектировании и разработке.
4.3.Оценка качества АС в установившемся режиме.
Основным прямым показателем качества АС в установившемся режиме является установившаяся ошибка: eуст = hзад - hуст.
Отметим, что эта характеристика применяется только для систем, для которых определено заданное значение выходного сигнала. Например - следящие системы - в которых выходной сигнал должен в точности повторять входной сигнал системы. Отметим также, что показатель eуст вычисляется в конце переходного процесса и, очевидно, при затянутых переходных процессах его вычисление по графику переходной функции не всегда возможно. Поэтому обычно eуст определяются аналитически.
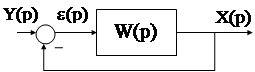
|
Рассмотрим следящую АС вида. Выходной сигнал этой системы e(р): 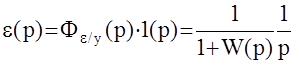 Напомним, что
Напомним, что 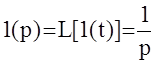 . Установившаяся ошибка может быть определена по второй предельной теореме :
. Установившаяся ошибка может быть определена по второй предельной теореме :
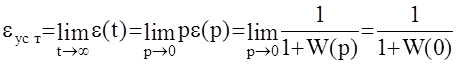 .
.
Определим значение W(0). Для этого допустим, что в общем случае
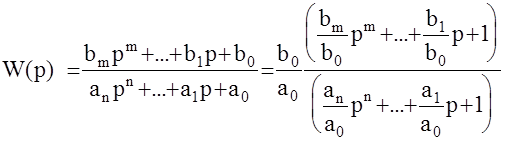 . Отсюда следует, что
. Отсюда следует, что 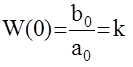 - коэффициент усиления разомкнутой системы. Таким образом получили, что для следящих систем величина установившейся ошибки обратно пропорциональна коэффициенту усиления разомкнутой системы.
- коэффициент усиления разомкнутой системы. Таким образом получили, что для следящих систем величина установившейся ошибки обратно пропорциональна коэффициенту усиления разомкнутой системы. 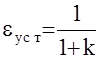 .
.
Увеличение коэффициента усиления k приводит к уменьшению eуст (т.е. увеличению статической точности ). Но с другой стороны, увеличение k приводит к снижению запаса устойчивости замкнутой системы, а следовательно к повышению колебательности и ухудшению других показателей качества. Это явление известно в автоматике как противоречие между статической точностью и устойчивостью и его разрешение явилось одной из предпосылок создания теории оптимального управления.
4.4.Анализ ошибок следящей системы при медленно меняющихся входных воздействиях.
Отметим, что медленно меняющимся будем называть сигнал, который имеет ограниченное число ненулевых производных.
Например: 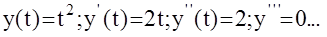
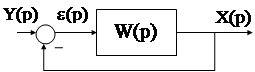
|
Пусть на вход следящей АС действует медленно меняющийся входной сигнал y(t). Определим вынужденную составляющую выходного сигнала e(t) в этом случае :
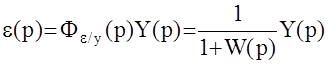 .
.
Представим передаточную функцию 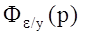 в виде бесконечного степенного полинома :
в виде бесконечного степенного полинома :
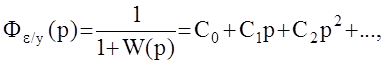 и определим условия, при которых возможно такое представление.
и определим условия, при которых возможно такое представление.
Пусть 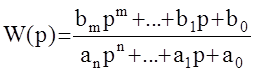 , тогда
, тогда 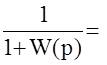
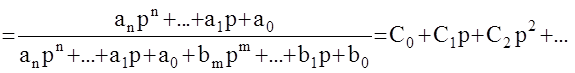
Приведем к общему знаменателю:

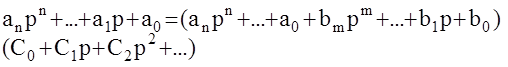

Раскроем справа скобки и сгруппируем члены при одинаковых степенях р
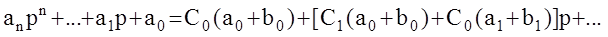
Два полинома равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях р
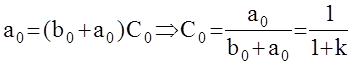
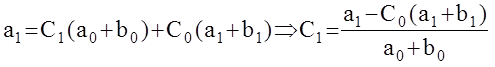
.............
Данные коэффициенты Ci получили название коэффициентов ошибок. Определив их, можно записать:
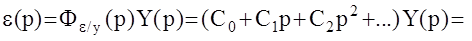
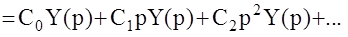
или переходя к оригиналам (при нулевых начальных условиях):
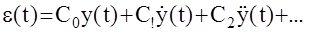
Необходимое число вычисляемых коэффициентов Ci определяется числом ненулевых производных входного сигнала.
Например: а) 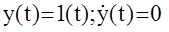
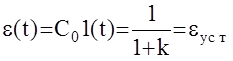 - известный результат;
- известный результат;
б) 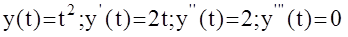
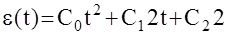 .
.
4.5.Статические и астатические системы
Для следящих систем очень важным является вопрос о безошибочном отслеживании входных сигналов, то есть в каких случаях установившаяся ошибка системы e(t) равна нулю? В соответствии с этим вводятся понятия статических и астатических систем.
АС называется статической по отношению к входному сигналу y(t), если при y(t)=Const установившаяся ошибка e(t) не равна нулю.
Так как в установившемся режиме

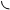


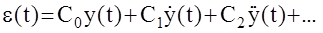 ,
,
= 0
то математическое условие статизма системы может быть записано так
С0¹ 0
АС называется астатической по отношению к входному сигналу
y(t) если при y(t)¹ 0, установившаяся ошибка e(t) равна нулю.
В зависимости от вида входного сигнала y(t) различают астатические АС:
- первого порядка ( y(t) = const, e(t) = 0);
- второго порядка ( y(t) =a + bt, e(t) = 0);
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
или математически:
-астатизм первого порядка С0= 0, С1¹ 0;
-астатизм второго порядка С0=0, С1=0, С2¹0;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.6.Структурные признаки астатизма.
Исходя из этих условий попробуем определить структурные признаки астатизма. Напомним, что если
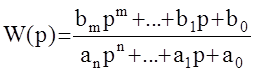 , то
, то 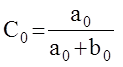 и если С0=0,
и если С0=0,
то а0 =0 - астатизм первого порядка .
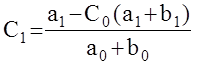 Þ если С0=0 и С1=0,
Þ если С0=0 и С1=0,
то а0=0 и а1=0 - астатизм второго порядка
. . . . . . . . . . . . . . . . . . . . . . . . . .
Или, переходя вновь к передаточной функции,
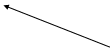



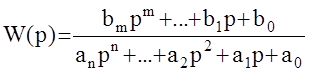 =0 -астатизм 1-го порядка - 1ин-
=0 -астатизм 1-го порядка - 1ин-
тегрирующее звено в разомкнутом контуре.
а1 =0 -астатизм 2-го порядка - 2 интегрирующихзвена.
Исходя из вышесказанного можно сформулировать следующий структурный признак астатизма системы:
Порядок астатизма АС по отношению к входному сигналу определяется числом интегрирующих звеньев в разомкнутом контуре системы.
|
Пример:
Порядок астатизма равен 1.
|
Однако, если мы будем увеличивать порядок астатизма, вводя всё новые интегрирующие звенья, то получим неустойчивую систему (система структурно неустойчива, если содержит два и более интегрирующих звена в разомкнутом контуре). Выход: одновременно с введением второго интегрирующего звена вводится одно форсирующее.
Пример:
|
Определим теперь структурный признак астатизма по отношению к возмущающему воздействию F(p).
Отметим, что в этом случае в качестве ошибки выступает сам выходной сигнал Х(р), то есть при действии возмущения F(p) система не должна на реагировать на это возмущение.
Допустим 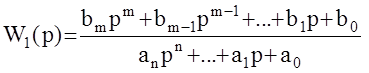 ;
;
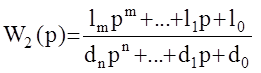 тогда
тогда
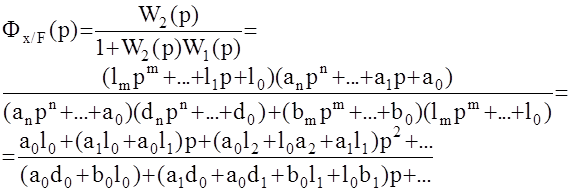
С другой стороны 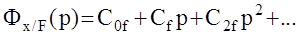
Приравнивая эти передаточные функции и, приведя к общему знаменателю, имеем
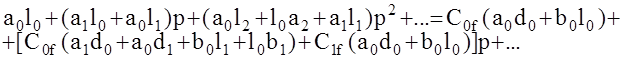
Из условия равенства полиномов имеем :
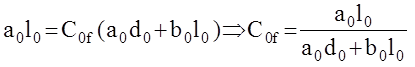
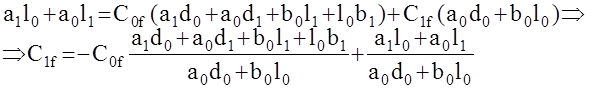
Как видим С0f = 0 (астатизм первого порядка по возмущению) будет в случае, если либо а0 = 0 либо l0 = 0, что соответствует наличию дифференцирующего ( l0 = 0) звена в прямой цепи от точки приложения возмущения к выходу системы или интегрирующего (а0= 0) звена в цепи от точки приложения возмущения к выходу против хода сигнала. Астатизм второго и более порядков обеспечивается наличием двух и более соответствующих звеньев.
|
Пример:
Более интересен вопрос, когда одновременно и а0 = 0 ; l0 = 0, то есть дифференцирующее звено в прямой и интегрирующее в обратной цепи.
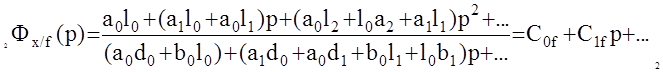 Сократим левую часть на р и приведем к общему знаменателю:
Сократим левую часть на р и приведем к общему знаменателю:
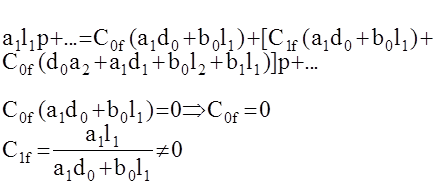
То есть получаем систему с астатизмом первого порядка по возмущению. Причем, астатизм второго порядка С1f = 0 достигается при условии либо а1 = 0 либо l1= 0 (то есть к условию наличия интегрирующего против хода и дифференцирующего по ходу, добавляется условие наличия еше одного интегрирующего либо дифференцирующего соответственно.) Таким образом в общем случае структурный признак астатизма системы по возмущению можно сформулировать следующим образом:
Порядок астатизма АС по отношению к возмущению определяется количеством интегрирующих звеньев, включенных между точкой приложения возмущения и выходом системы против хода сигнала, либо числом дифференцирующих звеньев по ходу. В случае если в системе одновременно есть и интегрирующие и дифференцирующие звенья, то порядок астатизма определяется наибольшим числом из этих звеньев.
Пример:
|
4.7.Косвенные показатели качества.Интегральная оценка качества.
Анализ АС с помощью только прямых показателей качества часто не дает желаемого эффекта. Прежде всего это связано с тем, что каждый из этих показателей характеризует только одну сторону переходных процессов. Так небольшое перерегулирование s может быть при очень большом времени регулирования tp или большой статической ошибке eуст. Иногда и сам вид переходной функции не известен и определить прямые показатели качества не представляется возможным. Поэтому возникает проблема создания некоторых обобщенных показателей качества без определения функции h(t).Такие показатели получили название косвенных. Из этой группы показателей наиболее широкое распространение получили интегральные оценки.
Интегральной оценкой качества переходного процесса называется интеграл вида 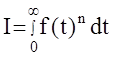 ,
,
где f(t) - абсолютно интегрируемая функция, характеризующая пере- ходный процесс в системе.
Напомним, что функция f(t) называется абослютно интегрируемой, если 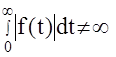 .
.
В качестве функции f(t) при анализе качества АС обычно используются : весовая функция g(t); ошибка системы e(t)=hж(t)-h(t); различные комбинации этих функций.
Поясним физический смысл интегральной оценки.
|
Интегральная оценка геометрически интерпретируется площадью под кривой f(t).Очевидно чем меньше эта площадь, тем быстрее затухает переходный процесс, тем лучше качество системы. Однако это не всегда так. Например, если h(t)
имеет слабое затухание, то есть неудовлетворительное качество, а оценка - сумма положительных и отрицательных площадей - может быть при этом маленькой. Более лучшей в этом смысле оценка 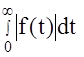 - сумма только положительных
- сумма только положительных
площадей. Однако на практике, наибольшее распространение получили оценки 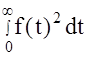 , в которых наибольший вес имеет начало переходного процесса, где вычисляются основные показатели качества(tp, s, tср, ...).Такие оценки получили название интегральных квадратичных оценок качества (ИКО), которые мы и будем рассматривать в дальнейшем. Вычисление ИКО можно осуществлять двумя методами: впрямую, вычисляя интеграл по известному виду f(t)2, либо используя методику Мандельштамма по известному изображению F(p).
, в которых наибольший вес имеет начало переходного процесса, где вычисляются основные показатели качества(tp, s, tср, ...).Такие оценки получили название интегральных квадратичных оценок качества (ИКО), которые мы и будем рассматривать в дальнейшем. Вычисление ИКО можно осуществлять двумя методами: впрямую, вычисляя интеграл по известному виду f(t)2, либо используя методику Мандельштамма по известному изображению F(p).
4.8.Корневые оценки качества
Рассмотрим ПФ устойчивой АС, не имеющей нулей
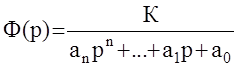 .
.
Если АС устойчива, то все ее полюса лежат в левой части комплексной плоскости, причем все они действительные либо комплексно сопряженные. Качество АС приближенно можно оценить двумя параметрами: степенью или запасом устойчивости h и степенью колебательности m.
|
Степень устойчивости h равна удалению от мнимой оси ближайшего полюса АС (или пары полюсов).
Степень колебательности m=tgj, где j - половина минимального центрального угла, внутри которого лежат все полюса системы.
Отметим, что качество системы определяется еще и тем какой корень или пара является ближайшим к мнимой оси. Если ближайший - вещественный корень, то говорят, что в системе доминирующей является передаточная функция 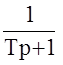 и степень устойчивости
и степень устойчивости 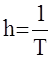 апериодическая. В этом случае время регулирования приближенно оценивается по формуле
апериодическая. В этом случае время регулирования приближенно оценивается по формуле 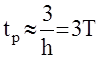 .
.
Если ближайшей является пара комплексно-сопряженных полюсов, то говорят, что в системе доминирующей является передаточная функция 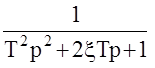 , где 0<x<1 и качество системы в целом оценивается этим звеном. Время регулирования при этом
, где 0<x<1 и качество системы в целом оценивается этим звеном. Время регулирования при этом 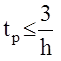 .
.
Определим степень устойчивости колебательного звена :
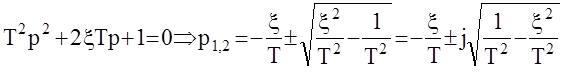
Запас устойчивости 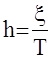 , тогда время регулирования
, тогда время регулирования 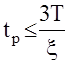 .
.
Значение степени колебательности m дает приближенную оценку перерегулирования в системе 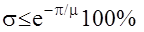 - формула Цыпкина.
- формула Цыпкина.
Если ПФ системы содержит помимо полюсов и нули, то влияние их на качество учитывается следующим образом:
1. Близко расположенные нули и полюса взаимно компенсируют друг друга. Причем считается, что нуль gi компенсирует полюс li , если
êli - gi ê£ 0,1 êli ê » 0,1 êgi ê
2. Близкие к началу координат нули, если они не компенсируются полюсами, увеличивают перерегулирование и время регулирования системы.
4.9.Полоса пропускания АС.
Полосой пропускания АС называется диапазон частот, в котором
мощность выходного сигнала АС уменьшается не более чем в 2
раза по отношению к мощности на частоте w=0.
Определяется полоса пропускания по амплитудно-частотной характеристике системы и задается частотой wP -верхней границей полосы пропускания.
Так как мощность сигнала N прямопропорциональна квадрату его амплитуды, то согласно определению полосы пропускания
|
|
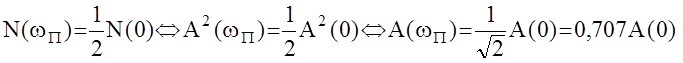 A(w)- АЧХ системы.Если перейти к ЛАЧХ L(w)=20lgA(w); L(wP)= 20lg(0,707A(0)) =20lgА(0) + 20lg0,707 = 20lgA(0) - 3дБ
A(w)- АЧХ системы.Если перейти к ЛАЧХ L(w)=20lgA(w); L(wP)= 20lg(0,707A(0)) =20lgА(0) + 20lg0,707 = 20lgA(0) - 3дБ
Таким образом, полоса пропускания -это диапазон частот, в котором амплитудно- частотная характеристика уменьшается в Ö2 раз или ЛАЧХ уменьшается на 3gБ.
4.10Оценка качества АС по виду ЛАЧХ разомкнутой системы.
На практике обычно АС задается своей передаточной функцией, по которой всегда можно построить логарифмические частотные характеристики. Причем для минимально фазовых систем достаточно знание одной ЛАЧХ. Возникает вопрос оценки качества АС по виду этой характеристики.
Рассмотрим решение этого вопроса на примере АС второго порядка
|
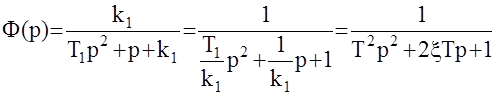
Где 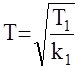 - постоянная времени замкнутой системы;
- постоянная времени замкнутой системы;
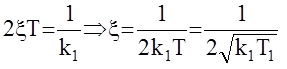 - относительный коэффициент затухания замкнутой АС.
- относительный коэффициент затухания замкнутой АС.
Параметры Т и x полностью определяют качество переходных процессов в замкнутой системе
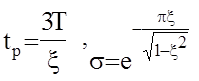 и чем меньше x тем хуже качество(tp,s). Рассмотрим два возможных вида ЛАЧХ разомкнутой системы:
и чем меньше x тем хуже качество(tp,s). Рассмотрим два возможных вида ЛАЧХ разомкнутой системы:
|
Можно сказать, что эти виды ЛАЧХ отвечают условиям :
1/Т1<wc 1/Т1>wc
Так как низкочастотная асимптота пересекает ось абсцисс на частоте
wс=k1 (интегрирующее звено), то данные условия можно записать так:
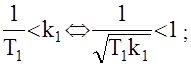
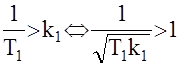
Учитывая, что 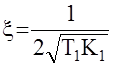 , можно записать :
, можно записать :
x < 0,5 x > 0,5
Для колебательного звена при x < 0,5 характерно существенное перерегулирование s ³ 20% и большое время регулирования tp³ 6T.
Поэтому, если обобщить полученные результаты, можно сделать следующий вывод: для систем, у которых частота среза wс приходится на участок с наклоном - 40дБ/дк, характерно низкое качество и даже неустойчивость.
Рассмотрим типовую ЛАЧХ разомкнутой системы:
|
Весь диапазон частот разбивается на три части: низкочастотную до w1 -наименьшая частота сопряжения, высокочастотная от w3 -ближайшая справа к частоте среза, среднечастотная от w1 до w3
Качество АС определяется по виду ЛАЧХ в каждом из этих диапазонов.
1.Низкочастотная асимптота определяется коэффициентом усиления
разомкнутой системы k и числом интегрирующих звеньев n, поэто-
му по ней однозначно определяются порядок астатизма системы n
и установившаяся ошибка 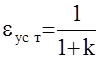 .
.
2.Основные показатели качества tp и s определяются по среднечас-
тотной асимптоте.Эти характеристики неудовлетворительны, если
наклон ее на частоте среза превышает - 20дБ/дк. Частота среза оп-
ределяет быстродействие системы. Чем больше wс, тем выше быст-
родействие, тем меньше время регулирования tp.
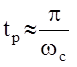
Частоты w3, w2, wс определяют перерегулирование в системе. Так s не превышает 20% если удовлетворяются равенства:
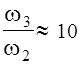 ;
; 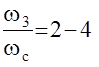 .
.
3.Высокочастотная асимптота не оказывает существенного влияния на
качество системы, однако чем круче ее наклон, тем лучше фильт-
рующие свойства.
Более точно характеристики качества по виду ЛАЧХ определяются по графикам, называемым номограммами Чесната-Майера, приводимых в специальных справочниках.
| <== предыдущая лекция | | | следующая лекция ==> |
| Если линейная стационарная АС устойчива, то все коэффициенты её характеристического полинома положительны. | | | Синтез линейных АС классическими методами. |
Дата добавления: 2015-12-16; просмотров: 1569;