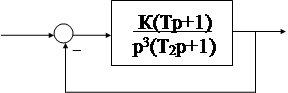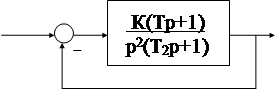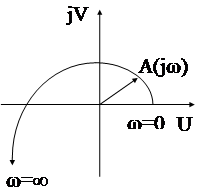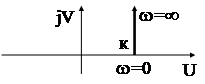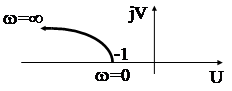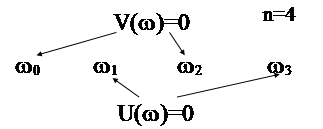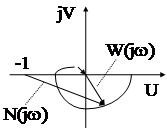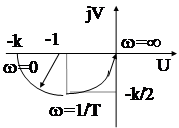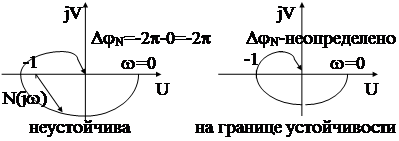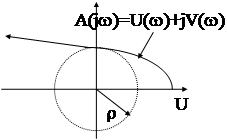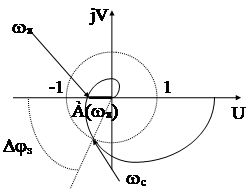Если линейная стационарная АС устойчива, то все коэффициенты её характеристического полинома положительны.
Из необходимого условия следует, что:
1) если, хотя бы один из коэффициентов характеристического полинома ai £ 0, то система неустойчива;
2) если все ai > 0, то факт устойчивости необходимо дополнительно исследовать другими методами.
Примеры: А(р) = р3 - 2р2 + р + 1 - неустойчива: а2 =-2 < 0;
А(р) = р3 + 2р2 + 1 - неустойчива: а1 = 0;
А(р) = 10р3 + 2р2 + 2р + 1 - необходимо дополнительное исследование устойчивости.
3.4Структурная неустойчивость
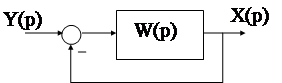
|
Исследуем с помощью полученного необходимого условия устойчивость АС вида: пусть передаточная функция разомкнутой АС имеет вид:
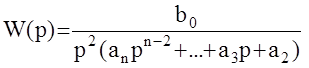 , то есть содержит два интегрирующих звена. Тогда передаточная функция замкнутой системы равна:
, то есть содержит два интегрирующих звена. Тогда передаточная функция замкнутой системы равна:
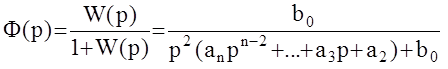 , а её характеристический полином:
, а её характеристический полином: 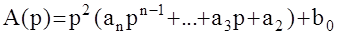 имеет коэффициент при р равный нулю, следовательно по необходимому условию данная система, содержащая два и более интегрирующих звена в разомкнутом контуре, является неустойчивой.
имеет коэффициент при р равный нулю, следовательно по необходимому условию данная система, содержащая два и более интегрирующих звена в разомкнутом контуре, является неустойчивой.
В общем виде признак структурной неустойчивости АС можно сформулировать так:
АС, разомкнутый контур которой включает интегрирующих звеньев на два больше чем форсирующих, неустойчива.
Отметим, что никаким изменением параметров структурно неустойчивые системы нельзя сделать устойчивыми - надо изменять их структуру. Стуктурно устойчивые же системы можно сделать как устойчивыми так и неустойчивыми, за счет изменения их параметров.
|
Примеры:
3.5Алгебраические критерии устойчивости. Критерий Гурвица.
Необходимое условие устойчивости - положительность коэффициентов характеристического полинома - к сожалению не является достаточным. Поэтому возникает вопрос, как дополнить это условие, опять же не находя полюса системы? Ответ на этот вопрос дают специальные критерии устойчивости, которые условно подразделяются на две большие группы: алгебраические (Вышнеградского, Гурвица, Рауса,...) и частотные (Михайлова, Найквиста,...). рассмотрим отдельные из этих критериев.
Критерий Гурвица: Для того чтобы замкнутая АС с характеристическим полиномом А(р)=аnpn+...+a1p+a0 была устойчивой, необходимо и достаточно , чтобы при an > 0 все главные диагональные миноры специально составленной матрицы Гурвица были положительны.
| Матрица Гурвица заполняется следующим образом: а) заполняется главная диагональ, начиная с а0 и заканчивая an-1; б) заполняются столбцы: вниз от главной диагонали коэффи- |
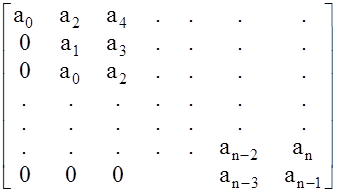
циенты с убывающими индексами, вверх - с возрастающими. Коэффициенты с индексами меньше 0 и больше n считаются нулевыми.
Напомним, что главным диагональным минором Мк называется определитель, стоящий на пересечении её к последовательных строк, начиная с первой, и к соответствующих столбцов.
Пример 1: А(р)=а2р2+а1р+а0

 М1 М2
М1 М2
     а0 а2 а0 а2
   0 а1 0 а1
|
Матрица Критерий Гурвица: аn = a2 > 0;
Гурвица: . М1=а0 > 0;
. M2=a0a1>0=> a1 > 0.
Следствие 1: Для устойчивоси АС второго порядка и ниже необходимое условие устойчивости 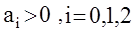 становится и достаточным.
становится и достаточным.
Пример 2 : 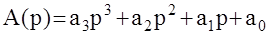
М1 М2 М3
        а0 а2 0 а0 а2 0
 0 а1 а3 0 а1 а3
   0 а0 а2 0 а0 а2
|
Критерий Гурвица:
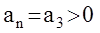 ;
;
M1=a0 > 0 ;
M2 = a0a1 > 0 => a1 > 0;
M3 = a0(a1a2 - a0a3)> 0 => a2>0,a1a2>a0a3 .
Эти соотношения определяют условия устойчивости АС третьего порядка, которые получили название критерия Вышеградского.
Следствие 2 : Для того чтобы АС третьего порядка была устойчивой необходимо и достаточно, чтобы при выполнении необходимого условия устойчивости произведение средних коэффициентов было больше произведения крайних.
Критерий устойчивости Рауса, как и критерий Гурвица, требует составления специальной матрицы. Однако в отличие от матрицы Гурвица элементы матрицы Рауса вычисляются по специальным формулам и об устойчивости системы судят по положительности всех коэффициентов первого столбца. Достоинство этого критерия в том, что нет необходимости вычислять определители больших порядков, а формулы вычисления коэффициентов в общем виде легко реализуются на ЭВМ.
3.6. Частотные критерии устойчивости. Критерий устойчивости Михайлова.
Алгебраические критерии устойчивости, связанные с анализом коэффициентов характеристического полинома, становятся при больших n достаточно громоздкими, что при отсутствии ЭВМ требует значительных временных и трудовых затрат. Кроме того, они не позволяют оценить насколько близко система находится от границы устойчивости, то есть не позволяют дать количественную оценку устойчивости. Поэтому естественен поиск других критериев более наглядных и не столь громоздких в вычислительном отношении. Попробуем воспользоваться для анализа устойчивости частотными характеристиками системы, а полученные критерии в соответствии с этим также назовем частотными.
В 1938 году советский ученый Михайлов предложил для оценки устойчивости использовать функцию:
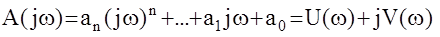 ,
,
получающуюся заменой переменной р в характеристическом полиноме замкнутой системы на комплексную переменную jw .
На комплексной плоскости функция Михайлова A(jw) представляется вектором. Траектория конца этого вектора при изменении частоты w от 0 до ¥ называется кривой Михайлова .Вид этой кривой определяется расположением корней характеристического полинома на комплексной плоскости, то есть связан с устойчивостью системы.
Теорема Михайлова: Для того чтобы линейная стационарная АС n-порядка была устойчивой необходимо и достаточно, чтобы вектор функции Михайлова A(jw) при изменении частоты от 0 до ¥ повернулся вокруг начала координат против часовой стрелки, нигде не обращаясь в ноль, на угол np/2
|
Доказательство : Так как характеристический полином А(р) n-степени имеет n корней , то он может быть представлен в виде: 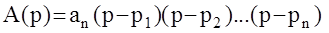 , где
, где 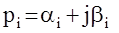 -корни полинома - либо действительные, либо комплексно сопряженные. Соответствующая функция Михайлова имеет вид:
-корни полинома - либо действительные, либо комплексно сопряженные. Соответствующая функция Михайлова имеет вид:
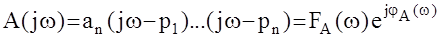 , где
, где
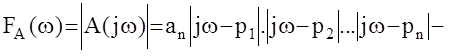 модуль функции Михайлова.
модуль функции Михайлова.
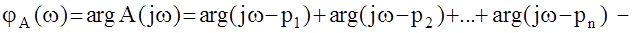
аргумент функции Михайлова.
Модуль FA(w) обращается в ноль тогда и только тогда, когда хотя бы один из сомножителей ½jw-pi½ обращается в ноль.
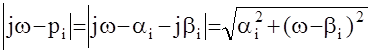 , поэтому если ai<0, то ни один из этих сомножителей в ноль не обращается.
, поэтому если ai<0, то ни один из этих сомножителей в ноль не обращается.
Рассмотрим как изменяется аргумент элементарной комплексной функции jw-pi при изменении частоты от 0 до ¥
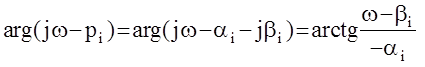 .
.
а) Если pi - корень действительный (bi = 0) , то при w = 0 arctg 0=0,
при w=¥ arctg ¥/-ai= arctg¥= +p/2 , если ai <0;
б) если p1 и p2 - пара комплексно сопряженных полюсов.
P1 =a+jb
p2 =a-jb
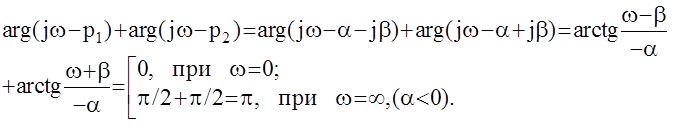
Следовательно, если ai<0 , то полное приращение аргумента функции Михайлова ( при изменеии частоты от 0 до ¥) равно np/2 .Таким образом если все корни характеристического полинома системы имеют отрицательные действительные части (ai<0 ),то функция Михайлова нигде не обращается в ноль, а полное приращение ее аргумента равно np/2 , что доказывает справедливость рассматриваемой теоремы.
|
Примеры:1) A(p) = k(Tp+1) n=1 ; DjA=p/2; FA(w) ¹ 0 - система устойчива.
2) 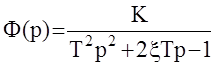 w=0 V(w)=0 ; U(w)=-1
w=0 V(w)=0 ; U(w)=-1  w=¥ V(w)=+¥; U(w)=-¥
w=¥ V(w)=+¥; U(w)=-¥
|
n=2 ;DjA=-p/2;FA(w)¹0- система неустойчива.
3.7 Следствие критерия Михайлова.
Рассмотрим кривые Михайлова для АС четвертого порядка:
      Неустойчива Неустойчива
|
   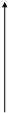  Устойчива Устойчива
|
В соответствии с критерием Михайлова кривая Михайлова для устойчивой АС проходит последовательно через четыре квадранта, пересекая по очереди в точках w0; w1; w2; w3 каждую из осей координат.Для устойчивой АС эта очередность нарушается. Отметим, что частоты w0; w1; w2; w3 удовлетворяют одному из двух уравнений V(w)=0 или U(w)=0 , то есть являются их корнями. Исходя из этого, можно сформулировать следующее следствие критерия Михайлова.
Следствие: Для того, чтобы линейная стационарная АС была устойчивой необходимо и достаточно, чтобы действительные корни wi ее многочленов V(w) и U(w) , расставленные в порядке возрастания чередовались между собой , и их число равнялось n - порядку системы.
|
Достоинство следствия критерия Михайлова в том, что он позволяет перейти от решения уравнения n - порядка к двум уравнениям меньшего порядка, что гораздо проще.
3.8. Критерий устойчивости Найквиста.
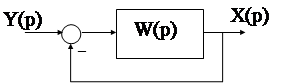 На практике обычно система задается передаточной функцией разомкнутой системы W(p). Поэтому возникает вопрос о возможности оценки устойчивости замкнутой системы по характеристикам разомкнутой. Для этого как раз и служит критерий Найквиста, предложенный в 30-х годах американским ученым.
На практике обычно система задается передаточной функцией разомкнутой системы W(p). Поэтому возникает вопрос о возможности оценки устойчивости замкнутой системы по характеристикам разомкнутой. Для этого как раз и служит критерий Найквиста, предложенный в 30-х годах американским ученым.
Пусть 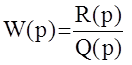 - передаточная функция разомкнутой системы. Причем следует отметить, что в разомкнутом состоянии система может быть и неустойчивой, то есть корни полинома Q(p) могут быть нулевыми или с положительными действительными частями. Возникает вопрос, когда будет устойчива замкнутая АС?
- передаточная функция разомкнутой системы. Причем следует отметить, что в разомкнутом состоянии система может быть и неустойчивой, то есть корни полинома Q(p) могут быть нулевыми или с положительными действительными частями. Возникает вопрос, когда будет устойчива замкнутая АС?
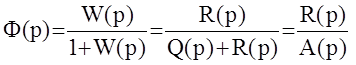 ,
,
здесь А(р) - характеристический полином замкнутой системы.
Для оценки устойчивости Найквист предложил ввести в рассмотрение следующую функцию (функцию Найквиста ):
|
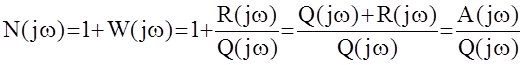 ,
,
равную отношению функций Михайлова замкнутой и разомкнутой АС. На графике функция Найквиста представляется как АФЧХ разомкнутой системы W(jw) , но с началом координат , сдвинутым влево в точку (-1, j 0) .
Полное приращение аргумента функции Найквиста определяется так:
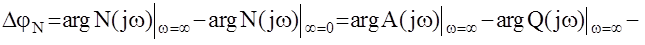
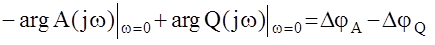 , где
, где
DjA - полное приращение аргумента функции Михайлова замкнутой системы;
DjQ- полное приращение аргумента функции Михайлова разомкнутой системы.
Сформулируем теперь собственно критерий Найквиста:
Замкнутая АС устойчива тогда и только тогда, когда полное приращение аргумента функции Найквиста DjN равно kp , где k -число полюсов разомкнутой АС с положительной действительной частью.
Доказательство : Пусть разомкнутая АС содержит k полюсов с положительной действительной частью, тогда полное приращение аргумента ее функции Михайлова определяется так :
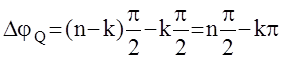
(n - k) - число полюсов с отрицательной действительной частью, каждый из которых дает приращение на +p/2;
k - число полюсов с положительной действительной частью, каждый из которых дает приращение на -p/2.
Если замкнутая АС устойчива, тогда полное приращение аргумента ее функции Михайлова равно 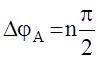 .
.
Согласно выведенному, полное приращение аргумента функции Найквиста равно: 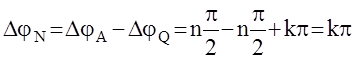 ,что и требовалось доказать.
,что и требовалось доказать.
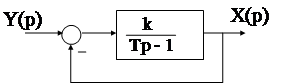
|
Пример : В разомкнутом состоянии АС неустойчива, имеет один корень (k=1) 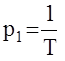 с положительной действительной частью. АФЧХ разомкнутой АС имеет вид:
с положительной действительной частью. АФЧХ разомкнутой АС имеет вид:
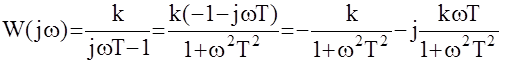
|
 w = 0; U(w) =-k; V(w) = 0
w = 0; U(w) =-k; V(w) = 0
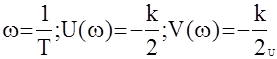
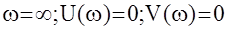 и так как число положительных полюсов равно 1, то - система устойчива в замкнутом состоянии (при условии k>1).
и так как число положительных полюсов равно 1, то - система устойчива в замкнутом состоянии (при условии k>1).
3.9.Следствия критерия Найквиста.
Если АС устойчива или нейтральна в разомкнутом состоянии, то следовательно число полюсов с положительной действительной частью равно нулю. В этом случае критерий Найквиста гласит, что для устойчивости замкнутой АС DjN=0 . Из этого вытекает следующее следствие критерия Найквиста.
|
Следствие 1. Замкнутая АС устойчива тогда и только тогда, когда годограф АФЧХ ее разомкнутой части ( устойчивой или нейтральной), не схватывает точку с координатами (-1, j0).
Выведем теперь второе следствие критерия Найквиста.
Рассмотрим АФЧХ разомкнутой системы и введем понятия следующих частот.
Частотой среза называется частота , на которой амплитудно частотная характеристика разомкнутой АС равна 1.
|
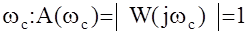
Частотой wp называется частота, на которой фазо-частотная характеристика системы равна -p.
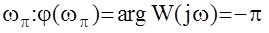
В соответствии с введенными обозначениями можно сформулировать следующее следствие критерия Найквиста.
Следствие 2. Замкнутая АС устойчива тогда и только тогда, когда она устойчива или нейтральна в разомкнутом состоянии и выполняется условие wс < wp .
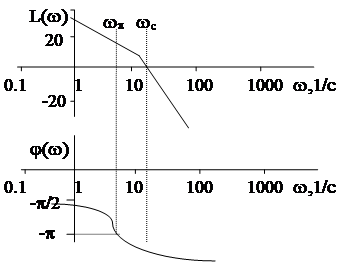
|
На практике часто для определения частот wс и wp применяются логарифмические частотные характеристики. В частности, для представленной АС: wс > wp -система в замкнутом состоянии неустойчива.
3.10.Запасы устойчивости АС.
На практике часто возникает задача не просто оценить устойчивость системы, но и дать некоторую количественную оценку устойчивости. Такая оценка получила название запаса устойчивости. Очевидно, способ задания или определения запаса устойчивости зависит от используемого критерия устойчивости.
|
Если известны полюса системы (необходимое и достаточное условие устойчивости), то запас устойчивости определяется как расстояние от мнимой оси ближайшей пары комплексно сопряженных полюсов или ближайшего действительного полюса. Эта характеристика обозначается через h.
|
При использовании критерия Михайлова запас устойчивости задаётся в виде некоторого числа r - соответствующего максимальному радиусу окружности с центром в начале координат, которую можно вписать в область, охватываемую кривой Михайлова.При заданном запасе устойчивости r кривая Михайлова не должна пересекать окружность и удовлетворять условиям устойчивости. Очевидно, запас устойчивости будет обеспечен, если для всех w выполняется 
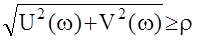 .
.
|
При использовании критерия устойчивости Найквиста запас устойчивости задаётся в виде двух величин: запас устойчивости по амплитуде и запас устойчивости по фазе. Нахождение замкнутой АС на границе устойчивости характеризуется системой двух уравнений
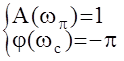
Запасом устойчивости по фазе называется угол, на который нужно довернуть АФЧХ разомкнутой АС так, чтобы замкнутая АС оказалась на границе устойчивости :Djз=argW(jw) = j(wc)+p.
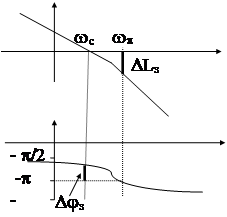
Запасом устойчивости по амплитуде называется значение АЧХ на частоте wp . Обычно эти запасы устойчивости определяются по логарифмическим частотным характеристикам
Djз = p + j(wс) , DLз = -20lg A(wp).
|
В данном случае система устойчива с запасами DLз и Djз . Можно показать, что с увеличением коэффициента усиления разомкнутой системы запасы устойчивости уменьшаются.
Дата добавления: 2015-12-16; просмотров: 1599;