Устойчивость линейных автоматических систем

3.1Определение устойчивости движения

Автоматические системы при нормальной эксплуатации должны поддерживать заданный режим работы объекта регулирования при действии на него различных возмущающих факторов. Такое поведение может быть достигнуто лишь в системах автоматического управления, обладающих устойчивостью по отношению к этим воздействиям. Устойчивость системы означает, что малые отклонения входных сигналов, начальных условий или параметров системы приводят к ограниченным отклонениям выходного сигнала. Физическое понятие устойчивости можно рассмотреть на классическом примере: «шарик - поверхность». В первом случае, малейшее отклонение шарика от положения равновесия приводит к появлению нарастающего отклонения от этого положения и шарик никогда не вернется в исходное состояние. В этом случае система называется неустойчивой. Во-втором случае после прекращения действия возмущения шарик останавливается, но в произвольной точке плоскости.То есть система нейтральна или на границе устойчивости. В третьем случае после прекращения действия возмущения шарик вернется в некоторую окрестность от первоначального положения. Говорят система устойчива. И лишь в последнем случае шарик вернется точно в исходное состояние. Такая система называется асимптотически устойчивой. В дальнейшем, за исключением, специально оговариваемых случаев, под общим термином устойчивость будем понимать асимптотическую устойчивость объекта.

Определение: АС называется устойчивой, если она будучи выведенной из состояния невозмущенного движения или покоя некоторым возмущением, вновь возвращается к этому состоянию после прекращения действия возмущения.

3.2Устойчивость невозмущенного движения по Ляпунову.

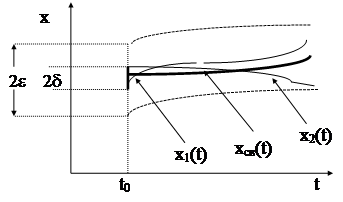
Математические основы теории устойчивости были разработаны выдающимся русским математиком и механиком А.М.Ляпуновым в начале ХХ века. Рассмотрим суть методов Ляпунова оценки устойчивости АС.Так как процессы в автоматических системах описываются дифференциальными либо разностными уравнениями, то математический анализ устойчивости сводится к исследованию решений таких уравнений. Как известно, общее решение неоднородного (с правой частью) дифференциального уравнения складывается из двух составляющих: общего решения однородного дифференциального уравнения х_св( t) и частного решения неоднородного уравнения х_вын(t). Составляющая х_вын(t) определяется видом входного сигнала y(t) и равна 0 при отсутствии последнего. Свободная или невозмущенная составляющая движения х_св( t) не зависит от приложенного входного сигнала, а определяется только свойствами самой системы и начальными условиями. Очевидно, что устойчивость, как свойство системы возвращаться в исходное состояние после прекращения действия возмущения, будет определяться видом только свободной составляющей движения, то есть АС устойчива тогда и только тогда, когда устойчиво ее невозмущенное движение.

Введем теперь определение устойчивости невозмущенного движения по Ляпунову. Решение х_св(t) устойчиво по Ляпунову при t®¥, если для любого e>0 и tÎ[0,¥) существует такое d=d(e,t₀)>0, что любое решение x(t), для которого при t=t₀ выполняется неравенство 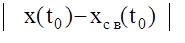<d, удовлетворяет неравенству 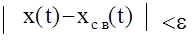. Геометрически это означает, что все траектории х(t), которые при t=t₀ начинаются в d-окрестности точки х_св(t₀) никогда не покинут e-трубку решения х_св(t), то есть ограниченные начальные условия приводят к ограниченным решениям.

Таким образом, определение устойчивости АС сводится к определению и анализу дифференциальных уравнений невозмущенного движения. Это и составляет суть первого метода Ляпунова (второй метод будет рассмотрен позже при анализе устойчивости многомерных и нелинейных АС).

На практике определение решений дифференциальных уравнений представляет достаточно трудоемкую задачу, поэтому первый метод Ляпунова в прямой постановке обычно не применяется, а сводится к использованию различных условий и критериев, позволяющих оценить устойчивость АС, не решая дифференциальных уравнений, ее описывающих.

3.3. Необходимые и достаточные условия устойчивости.

Согласно первому методу Ляпунова устойчивость линейных АС определяется решением однородного линейного дифференциального уравнения:

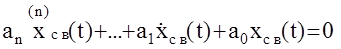
В общем случае решение данного уравнения имеет вид:

,

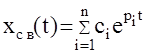где c_i -произвольные константы;

p_i- корни характеристического уравнения 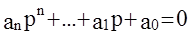. Для того чтобы система была устойчивой, очевидно должно выполняться условие:

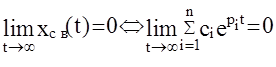В общем случае p_i= a_i + jb_i , тогда:

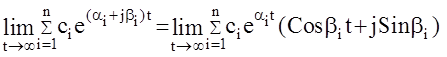. При любых t и b_i выражение в скобках есть величина ограниченная (модуль скобки всегда равен 1), следовательно всё это произведение стремится к нулю тогда и только тогда, когда стремится к нулю сомножитель 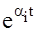, что возможно лишь при отрицательных значениях a_i . Таким образом, необходимое и достаточное условие устойчивости линейных стационарных АС можно сформулировать следующим образом.