ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Пусть требуется решить систему обыкновенных дифференциальных уравнений (СОДУ)

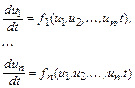
с начальными условиями

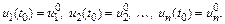
Это значит, что необходимо найти функции 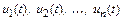на отрезке 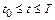такие, что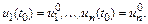

Запишем сформулированную задачу, ее называют задачей Коши для системы обыкновенных дифференциальных уравнений, в векторном виде:

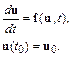
Решение задачи Коши заключается в нахождении такой траектории 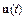, которая бы удовлетворяла условию .

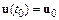Применение численных методов для решения задачи Коши предполагает приближенное вычисление значений в точках 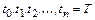отрезка 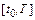. С этой целью СОДУ заменяют разностной схемой, из которой рекуррентно вычисляют приближенные значения .

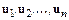Запишем общий вид разностной схемы:

.

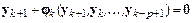Она связывает искомое решение 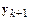в текущий момент времени 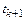с построенными к этому моменту времени решениями 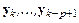в предыдущие моменты времени. Здесь 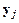– приближенное значение 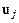, т. е. 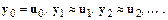Выбор функции 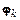в разностной схеме определяет соответствующий численный метод.

Приведем общую характеристику методов.

· Если 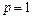, т. е.

,

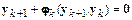то метод является одношаговым. Он связывает решение в последующий момент времени с решением в предыдущий момент времени. Если 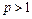, то метод является многошаговым.

· Метод является явным, если функция 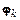не зависит от 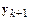и неявным в противном случае. В случае явного одношагового метода искомое решение 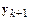на текущем шаге интегрирования вычисляется тривиально:

.

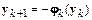Неявный одношаговый метод требует для расчета 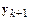решать систему в общем случае нелинейных алгебраических уравнений

,

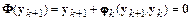привлекая, например, итерационную процедуру Ньютона.

· Различают локальную 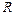и интегральную 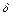погрешности метода. Локальная погрешность – ошибка на шаге интегрирования, интегральная погрешность – полная погрешность в текущий момент времени.

Обратимся к графической иллюстрации погрешности. Пусть численно решается уравнение

.

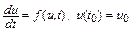В результате выполнения первого шага интегрирования (см. рис. 10.1) приближенное значение искомой функции в момент времени 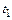равно

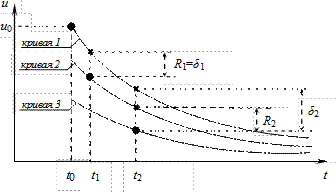
Рис. 10.1. Иллюстрация локальной и интегральной погрешностей

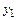. Это значение принадлежит некоторой интегральной кривой 2, являющейся решением дифференциального уравнения при другом, отличном от 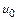, начальном условии. Разница между приближенным значением 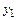и точным 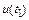составляет локальную погрешность. Очевидно, что на первом шаге локальная погрешность совпадает с интегральной погрешностью. Второй шаг интегрирования приводит к приближенному значению 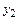, которое принадлежит интегральной кривой 3. Видно, что локальная погрешность на этом шаге, равная разности 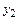и значения ординаты кривой 2 в момент времени 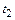, существенно отличается от интегральной погрешности – разности между приближенным 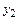и точным 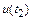значениями.

Наиболее объективной характеристикой точности метода является величина интегральной погрешности. К сожалению, выполнить ее оценку крайне сложно. На практике при выборе шага интегрирования обычно используют локальную погрешность численного метода.

· Если величина шага интегрирования 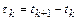ограничивается только допустимой локальной погрешностью 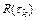метода, то такой метод является абсолютно устойчивым к шагу интегрирования. Метод, обладающий таким свойством, позволяет осуществлять выбор шага интегрирования, исходя лишь из требуемой точности. Условно устойчивый метод характеризуется тем, что шаг интегрирования ограничивается не только допустимой локальной погрешностью, но и определенными свойствами решаемой системы. Последние ограничения являются весьма обременительными для некоторых классов задач.

Рассмотрим разностные схемы наиболее широко используемых на практике методов численного интегрирования.