Методы Рунге–Кутта.

Точность явных одношаговых методов численного решения систем обыкновенных дифференциальных уравнений вида

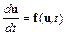
можно повысить, сохраняя в разложении функции 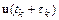в ряд Тейлора большее число членов. Например, метод второго порядка имеет следующую разностную схему:

,

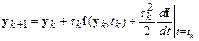или

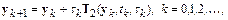
где

.

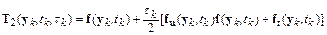Основное неудобство такой формы разностной схемы – необходимость вычисления частных производных 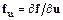, 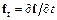. Эта трудность значительно возрастает при построении методов более высокого порядка точности.

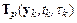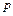В методах Рунге–Кутта функции , где – порядок точности метода, заменяются на некоторые удобно вычисляемые функции 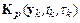таким образом, что

,

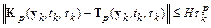где 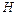– константа, не зависящая от .

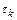В методе Рунге–Кутта второго порядка функция 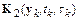имеет вид

.

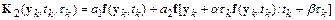Разложим функцию 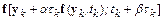в ряд Тейлора в окрестности точки :

.

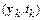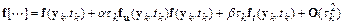Подставим это разложение в выражение для :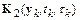

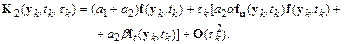
Сравнивая 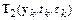и 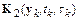, нетрудно видеть, что при

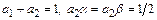
эти формы совпадают с точностью до члена .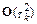

Если положить 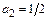, то 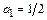, 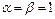. В результате метод Рунге–Кутта второго порядка примет вид:

,

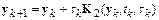где

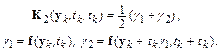
По аналогии можно построить методы Рунге–Кутта более высоких порядков. Не останавливаясь на выводе, приведем популярный на практике метод Рунге–Кутта четвертого порядка:

,

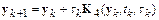где

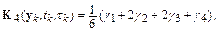
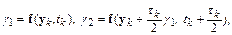
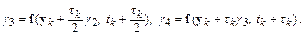
На каждом шаге интегрирования в методе Рунге–Кутта четвертого порядка приходится четырежды вычислять значение функции 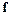при разных значениях аргументов. Более того, эти значения функции используются лишь однократно, что отражается на эффективности вычислений.

Методы Рунге–Кутта относятся к классу явных условно устойчивых методов. По этой причине они оказываются неприемлемыми для решения жестких систем обыкновенных дифференциальных уравнений.