Неявные многошаговые методы Адамса.

Неявный метод Адамса 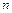-го порядка получается из общей разностной схемы линейных многошаговых методов при условии

,

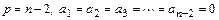т. е.

.

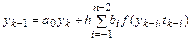Здесь 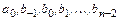, их всего 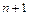, определяются из условий корректности полиномиальных решений 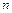-го порядка.

Как и в явных методах Адамса, 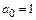. Обозначим 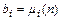, , 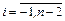подчеркивая тем самым зависимость значений коэффициентов 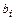от порядка метода. Подставим выбранные значения параметров в условие корректности:

.

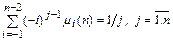Относительно неизвестных коэффициентов 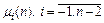получим систему из 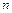линейных алгебраических уравнений:

.

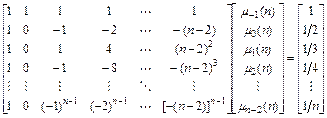Решение этой системы однозначно определяет коэффициенты неявного метода Адамса 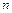-го порядка.

Запишем неявные методы Адамса первого, второго и третьего порядков.

1. 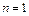. Коэффициент 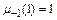и

.

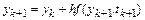Разностная схема неявного метода Адамса первого порядка совпадает с неявным методом Эйлера.

2. 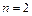. В этом случае

,

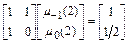и искомые коэффициенты имеют следующие значения: 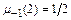, 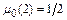. Неявный метод Адамса второго порядка

,

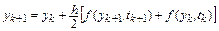как легко видеть, является методом трапеций.

3. 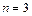. Коэффициенты 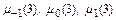вычисляются в этом случае из системы

.

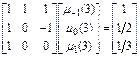Ее решение: 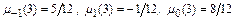. Неявный метод Адамса третьего порядка принимает вид:

.

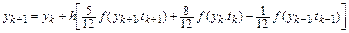Запись неявных методов Адамса более высоких порядков точности можно продолжить по аналогии.

Приведем теперь без вывода соотношение для расчета локальной погрешности неявного метода Адамса 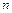-го порядка:

,

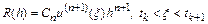где значения коэффициента 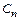для рассмотренных выше разностных схем соответственно равны: .

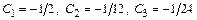Сравнивая явные и неявные методы Адамса одного порядка между собой, можно отметить, что методы имеют одинаковую по порядку, но разную по знаку локальную погрешность.