Условие устойчивости линейного многошагового метода.

Будем полагать теперь, что для решения тестового уравнения используется многошаговый метод. В этом случае

.

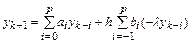Преобразуем это выражение следующим образом:

,

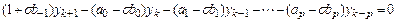где 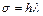.Введем подстановку

.

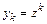Тогда разностное уравнение приводится к виду

,

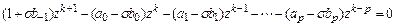или

.

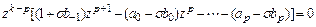Каждый корень полиномиального уравнения

,

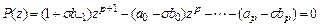их всего 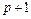для каждого фиксированного 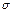, порождает частное решение 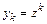разностного уравнения многошагового метода. Так как разностное уравнение многошагового метода линейно и для него справедлив принцип суперпозиции, общее решение в предположении, что все корни 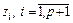различны, можно представить в виде

,

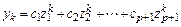где 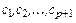– постоянные коэффициенты. Если полиномиальное уравнение 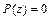содержит кратный корень 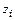кратности 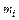, то соответствующий член в общем решении будет таким :

.

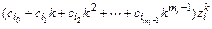Отсюда следует, что 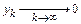, если 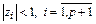. Таким образом, многошаговый метод является численно устойчивым для тех значений 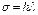, для которых 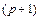корень полиномиального уравнения 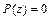лежит внутри единичной окружности .

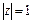Множество всех значений 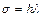, для которых многошаговый метод является численно устойчивым, называют областью устойчивости метода.