Алгебраический критерий устойчивости Рауса-Гурвица
Критерий устойчивости (условие наличия в характеристическом уравнении САР только отрицательных корней, или комплексно-сопряженных корней с отрицательной вещественной частью) был сформулирован швейцарским математиком А. Гурвицем в 1895 году. Критерий связывает расположение корней характеристического полинома
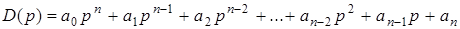
с определенными условиями, накладываемыми на его коэффициенты 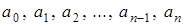 .
.
Для применения критерия необходимо из коэффициентов полинома составить матрицу Гурвица в следующем виде
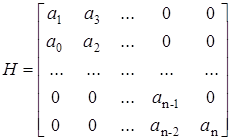 .
.
Матрица Гурвица составляется следующим образом. Диагональ матрицы заполняется по-порядку коэффициентами полинома начиная с 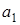 . Первая строка матрицы Гурвица заполняется коэффициентами полинома, имеющими нечетные индексы, вторая строка – коэффициентами, имеющими четные индексы (
. Первая строка матрицы Гурвица заполняется коэффициентами полинома, имеющими нечетные индексы, вторая строка – коэффициентами, имеющими четные индексы ( 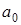 относится к коэффициентам, имеющим четные индексы), третья строка опять заполняется коэффициентами полинома, имеющими нечетные индексы и т.д. Свободные места в матрице заполняются нулями.
относится к коэффициентам, имеющим четные индексы), третья строка опять заполняется коэффициентами полинома, имеющими нечетные индексы и т.д. Свободные места в матрице заполняются нулями.
САР будет устойчива (в характеристическом полиноме будут все корни отрицательные, или с отрицательной вещественной частью), если положительны все диагональные миноры, полученные из матрицы Гурвица
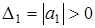 ;
; 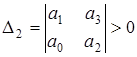 ;
; 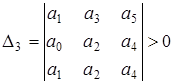 ;
; 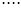 ;
; 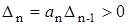 .
.
Примеры.
1). Для характеристического полинома 2-й степени 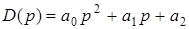 условие А.Стодолы
условие А.Стодолы 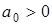 ,
, 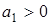 ,
, 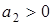 является необходимым и достаточным.
является необходимым и достаточным.
2). Для характеристического полинома 3-й степени  необходимыми и достаточными условиями устойчивости являются:
необходимыми и достаточными условиями устойчивости являются:
а) 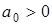 ,
, 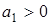 ,
, 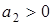 ,
, 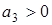 (условие А.Стодолы),
(условие А.Стодолы),
б) 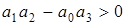 (получено по матрице А.Гурвица).
(получено по матрице А.Гурвица).
3). Для характеристического полинома 4-й степени 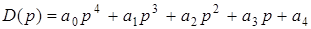 необходимыми и достаточными условиями устойчивости являются:
необходимыми и достаточными условиями устойчивости являются:
а) 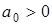 ,
, 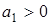 ,
, 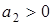 ,
, 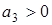 ,
, 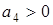 (условие А.Стодолы),
(условие А.Стодолы),
б) 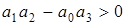 и
и 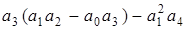 (получено по матрице А.Гурвица).
(получено по матрице А.Гурвица).
4). Для характеристического полинома 5-й степени 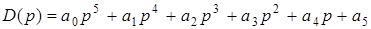 необходимыми и достаточными условиями устойчивости являются:
необходимыми и достаточными условиями устойчивости являются:
а) 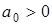 ,
, 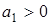 ,
, 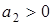 ,
, 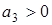 ,
, 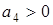 ,
, 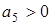
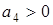 (условие А.Стодолы),
(условие А.Стодолы),
б) 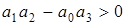 ,
, 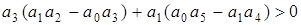 ,
,
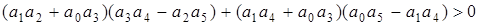 (получено по матрице А.Гурвица).
(получено по матрице А.Гурвица).
Дата добавления: 2015-12-22; просмотров: 2128;
