Частотный критерий устойчивости А.В.Михайлова

Критерий устойчивости (условие наличия в характеристическом уравнении САР только отрицательных корней, или комплексно-сопряженных корней с отрицательной вещественной частью) был сформулирован инженером А.В.Михайловым (СССР) в 1938 году. Критерий базируется на принципе аргумента функции комплексной переменной.

Для анализа устойчивости САР необходимо в ее характеристический полином

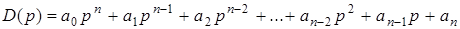
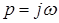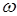подставить , где - частота ( 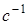), в результате получаем следующий характеристический комплекс

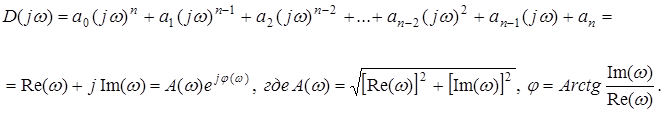
Вещественная часть комплекса 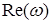будет содержать только четные степени 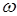, мнимая часть комплекса 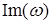будет содержать только нечетные степени 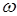. 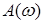называется модулем характеристического комплекса, 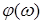- фазой (аргументом) характеристического комплекса.

Характеристический полином будет иметь только отрицательные (или комплексно-сопряженные с отрицательной вещественной частью) корни, если полное приращение аргумента (фазы) 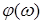при изменении 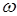от 0 до 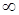составит 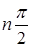, при этом САР является устойчивой. Если полное приращение аргумента (фазы) 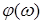при изменении 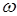от 0 до 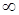будет меньше, чем 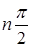, то в полиноме существуют положительные (или комплексно сопряженные с положительной вещественной частью) корни и тогда САР является неустойчивой.

Геометрически при изменении 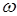от 0 до 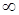характеристический комплекс на плоскости координат 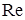и представляет собой годограф (годограф Михайлова), описываемый концом вектора с модулем (длиной вектора) 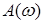и углом (фазой) .

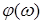Условием нахождения САР на границе устойчивости является прохождение годографа через начало координат, т.е. существует частота 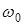, для которо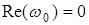й и 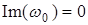. Если 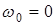(годограф начинается из начала координат) в полином существуют нулевые вещественные корни, если в полиноме существуют комплексно сопряженные корни с нулевой вещественной частью.

Для примера рассмотрим годографы Михайлова для трех САР со следующими полиномами

1) 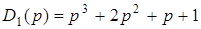; 2) ;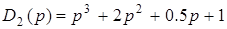

3) .

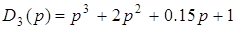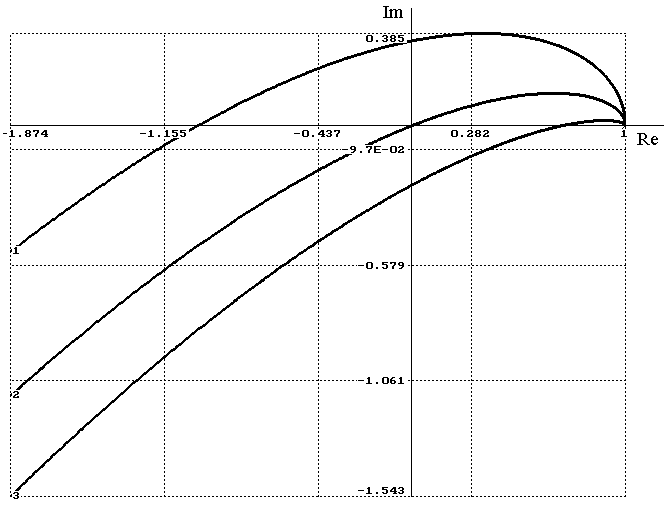
В соответствии с полученными годографами заключаем, что первая САР устойчива, вторая САР находится на границе устойчивости, третья САР является неустойчивой.