Неявные многошаговые методы Гира.

Неявный многошаговый метод Гира 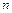-го порядка получается из общей разностной схемы многошаговых методов при следующем выборе параметров:

.

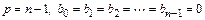Его разностная схема

.

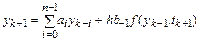Коэффициенты 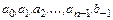должны быть определены таким образом, чтобы выполнялись условия корректности полиномиальных решений, которые, с учетом выбранных значений 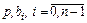, принимают вид

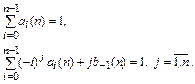
Запись 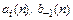подчеркивает зависимость значений этих коэффициентов от порядка метода.

Запишем условия корректности полиномиальных решений многошаговых методов Гира в развернутом виде:

.

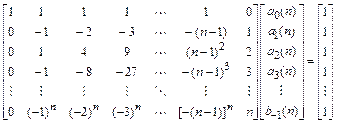Решение этой системы линейных алгебраических уравнений единственным образом определяет коэффициенты метода Гира 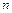-го порядка.

Приведем методы Гира первого, второго и третьего порядков.

1. 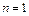. Коэффициенты 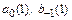определяются системой

,

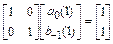из которой находим 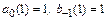, и разностная схема метода Гира записывается следующим образом:

.

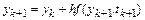Разностная схема метода Гира первого порядка совпадает с неявным методом Эйлера.

2. 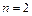. В этом случае неизвестные коэффициенты 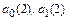, 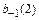являются решением системы

.

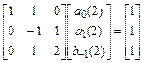Видно, что 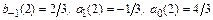. Разностная схема метода Гира второго порядка имеет вид

.

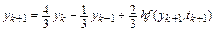3. 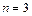. При этом система линейных алгебраических уравнений

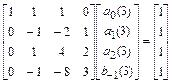
определяет следующие значения неизвестных коэффициентов: 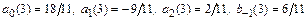. Подставив эти коэффициенты в общую формулу методов Гира, получим метод Гира третьего порядка:

.

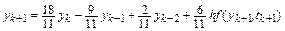По аналогии можно построить многошаговые методы Гира и более высоких порядков.

Приведем в заключение оценку локальной погрешности (без вывода) метода Гира 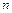-го порядка:

,

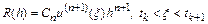где константа 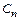зависит от порядка метода и для приведенных схем соответственно равна: .

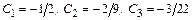Лекция 13