Явные многошаговые методы Адамса.
Этот класс методов легко получить из общей разностной схемы линейных многошаговых методов
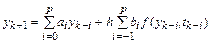
и условий корректного выбора коэффициентов
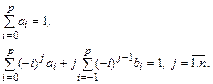
Полагая 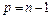 ,
, 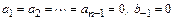 , получим разностную схему явного многошагового метода порядка
, получим разностную схему явного многошагового метода порядка 
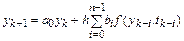 ,
,
где коэффициенты 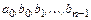 , их всего
, их всего 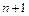 , однозначно определяются из
, однозначно определяются из 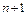 условия корректности.
условия корректности.
Из первого условия корректности находим
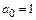 .
.
Обозначим 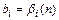 . Эта запись подчеркивает, что значение коэффи-циента
. Эта запись подчеркивает, что значение коэффи-циента 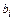 зависит от порядка метода. Чтобы определить
зависит от порядка метода. Чтобы определить 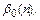
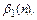
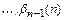 , подставим значения
, подставим значения 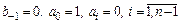 в оставшиеся
в оставшиеся 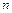 условий корректности:
условий корректности:
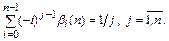
Получили систему из 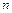 линейных алгебраических уравнений относи-тельно
линейных алгебраических уравнений относи-тельно 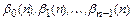 :
:
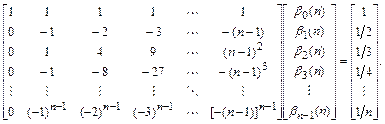
Запишем явные методы Адамса различных порядков.
1. 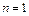 . Коэффициент
. Коэффициент 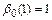 и
и
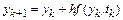 .
.
Разностная схема явного метода Адамса первого порядка совпадает с разностной схемой явного метода Эйлера.
2. 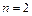 . Соотношения для
. Соотношения для 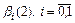 являются системой из двух линейных алгебраических уравнений
являются системой из двух линейных алгебраических уравнений
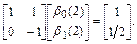
Следовательно 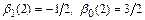 , и разностная схема явного метода Адамса второго порядка принимает вид
, и разностная схема явного метода Адамса второго порядка принимает вид
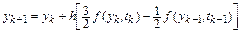 .
.
3. 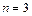 . Относительно
. Относительно 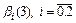 , запишем систему линейных алгебраических уравнений третьего порядка
, запишем систему линейных алгебраических уравнений третьего порядка

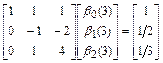 ,
,
из которой следует, что 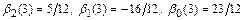 . В результате разностная схема явного метода Адамса третьего порядка записывается следующим образом:
. В результате разностная схема явного метода Адамса третьего порядка записывается следующим образом:
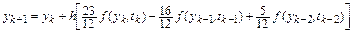 .
.
Этот процесс записи разностных схем явных многошаговых методов более высоких порядков точности можно продолжить и далее.
Не останавливаясь на выводе, приведем выражение для локальной погрешности явных многошаговых методов Адамса порядка 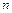 :
:
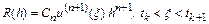 ,
,
где 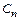 – постоянный коэффициент, величина которого зависит от метода, в частности
– постоянный коэффициент, величина которого зависит от метода, в частности 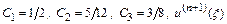 – значение
– значение 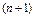 -й производной функции
-й производной функции 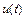 в точке
в точке 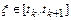 .
.
Дата добавления: 2015-11-24; просмотров: 824;
